
- •Учреждение образования «Высший государственный колледж связи»
- •Теория электросвязи
- •Раздел 1. Основы анализа сигналов.
- •1.1. Основные элементы функционального анализа сигналов. Норма и метрика.
- •1.2 Ортогональные сигналы. Ортонормированный базис. Обобщенный ряд Фурье
- •Раздел 2. Основы спектрального анализа сигналов
- •2.1 Теоремы о спектрах
- •2.3. Спектры модулированных сигналов.
- •2.3.1 Спектры амплитудно модулированных сигналов
- •2.3.2 Спектр сигналов с угловой модуляцией
- •Раздел 3. Аналитический сигнал и преобразования Гильберта
- •3.1 Аналитический сигнал. Основные понятия и определения. Спектр аналитического сигнала.
- •3.2 Преобразования Гильберта и его свойства. Применение пре образования Гильберта.
- •Раздел 4. Основы корреляционного анализа сигналов
- •4.1. Автокорреляционная функция сигналов
- •4.2. Взаимокорреляционная функция двух сигналов
- •Раздел 5. Основные элементы цифровой обработки сигналов
- •5.1. Дискретное преобразование Фурье
- •5.2. Быстрое преобразование Фурье
- •Раздел 6. Математические модели приема сигналов на фоне помех
- •6.1. Стационарные и эргодические случайные процессы.
- •6.2. Спектральное представление стационарных случайных процессов. Теорема Винера-Хинчина
- •Раздел 7. Математические модели приема сигналов на фоне помех (окончание)
- •7.1 Типовые модели случайных сигналов
- •7.2 Узкополосные случайные сигналы
- •Раздел 8. Основные сведения о шумоподобных сигналах
- •8.1 Шумоподобные сигналы и их свойства. Применение шумоподобных сигналов.
- •Раздел 9. Основы теории разделения сигналов
- •9.1 Основные положения линейной теории сигналов.
- •9.2 Структурная схема системы многоканальной передачи информации.
- •Раздел 10. Основные положения теории передачи информации
- •10.1 Информационные характеристики дискретных сообщений и сигналов
- •10.2 Взаимная информация
- •10.3. Информация в непрерывных сигналах. Дифференциальная энтропия.
- •10.4. Пропускная способность канала связи
- •10.5. Информация в непрерывных сообщениях. Эпсилон-энтропия
- •Раздел 11. Принципы оптимальной обработки сигналов на фоне помех
- •11.1. Задача оптимального приёма дискретных сообщений
- •11.2. Элементы теории решений
- •11.3. Критерии оптимизации приёма дискретных сообщений
- •11.4 Алгоритм оптимального приёма при полностью известных сигналах. (Когерентный приём)
- •Раздел 12. Принципы оптимальной обработки сигналов на фоне помех (продолжение)
- •16.5 Реализация алгоритма оптимального приема на основе корреляторов
- •12.2 Реализация алгоритма оптимального приёма на основе согласованных фильтров. Свойства согласованного фильтра
- •12.3 Потенциальная помехоустойчивость систем с различными видами манипуляции
- •Раздел 13. Принципы оптимальной обработки сигналов на фоне помех (окончание)
- •13.1 Оптимальный прием дискретных сообщений с неопределенной фазой (Некогерентный прием).
- •13.2 Помехоустойчивость систем с различными видами дискретной модуляции при некогерентном приеме
- •13.3 Прием дискретных сообщений в каналах с замираниями
- •Раздел 14. Основы цифровой обработки сигналов
- •14.1 Основные принципы цифровой фильтрации. Характеристики и свойства цифровых фильтров.
- •14.2 Алгоритм линейной цифровой фильтрации.
- •Тема 15. Основы цифровой обработки сигналов (окончание)
- •15.1 Трансверсальные цифровые фильтры.
- •15.2 Рекурсивные цф. Устойчивость цифровых фильтров
- •Раздел 16. Введение в вейвлет-преобразования сигналов
- •16.1 Понятие вейвлет-преобразования. Основные вейвлеты, применяемые в системах связи.
- •16.2 Дискретный вейвлет-анализ.
- •16.3 Непрерывное вейвлет-преобразование
- •Содержание.
Раздел 7. Математические модели приема сигналов на фоне помех (окончание)
7.1 Типовые модели случайных сигналов
А) Белый шум.
стационарный случайный процесс с постоянной на всех частотах спектральной плотностью мощности называется белым шумом.
 (7.1)
(7.1)
Термин «белый шум» образно подчёркивает аналогию с «белым» (естественным) светом, у которого в пределах видимого диапазона интенсивность всех спектральных составляющих приблизительно одинакова.
По теореме Винера-Хинчина функция корреляции белого шума:
 равна нулю всюду
кроме точки
равна нулю всюду
кроме точки
 .
Средняя мощность (дисперсия) белого
шума неограниченно велика.
.
Средняя мощность (дисперсия) белого
шума неограниченно велика.
Белый шум является
дельта-коррелированным процессом.
Некоррелированность мгновенных значений
такого случайного сигнала означает
бесконечно большую скорость изменения
их во времени – как бы мал ни был интервал
 ,
сигнал за это время может измениться
на любую наперёд заданную величину.
,
сигнал за это время может измениться
на любую наперёд заданную величину.
Белый шум является абстрактной математической моделью и отвечающий ему физический процесс, безусловно, не существует в природе. Однако это не мешает приближённо заменять реальные достаточно широкополосные случайные процессы белым шумом в тех случаях, когда полоса пропускания цепи, на которую воздействует случайный сигнал, оказывается существенно уже эффективной ширины спектра шума.
Б) Гауссово (нормальное) распределение.
В теории случайных сигналов фундаментальное значение имеет гауссова плотность вероятности.
 (7.2)
(7.2)
содержащая два
числовых параметра m
и
 .
График данной функции представляет
собой колоколообразную кривую с
единственным максимумом в точкеx=m.
При уменьшении
.
График данной функции представляет
собой колоколообразную кривую с
единственным максимумом в точкеx=m.
При уменьшении
 график всё более локализуется в
окрестности точкиx=m.
график всё более локализуется в
окрестности точкиx=m.

Непосредственным
вычислением можно убедиться, что
параметры гауссова распределения имеют
смысл соответственно математического
ожидания и дисперсии:
 ;
;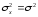 .
Функция распределения гауссовой
случайной величины
.
Функция распределения гауссовой
случайной величины

Замена переменной
 даёт:
даёт:
 (7.3)
(7.3)
Здесь Ф интеграл вероятностей

График функции F(x) имеет вид монотонной кривой, изменяющейся от 0 до 1.

7.2 Узкополосные случайные сигналы
Исследуем свойства
узкополосных случайных сигналов, у
которых спектральная плотность мощности
имеет резко выраженный максимум вблизи
некоторой частоты
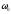 ,
отличной от нуля. Определим функцию
корреляции узкополосного случайного
процесса.
,
отличной от нуля. Определим функцию
корреляции узкополосного случайного
процесса.
Рассмотрим
стационарный случайный процесс x(t),
односторонний спектр мощности которого
 концентрируется в окрестности некоторой
частоты
концентрируется в окрестности некоторой
частоты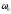 >0.
По теореме Винера-Хинчина функция
корреляции данного процесса
>0.
По теореме Винера-Хинчина функция
корреляции данного процесса
 (7.4)
(7.4)
Мысленно сместим
спектр процесса из окрестности частоты
 в окрестность нулевой частоты, выполнив
замену переменной
в окрестность нулевой частоты, выполнив
замену переменной .
Тогда формула (7.4) приобретает вид:
.
Тогда формула (7.4) приобретает вид:
 (7.5)
(7.5)

В соответствии с
исходным предположением об узкополосности
процесса X(t)
его спектр мощности
 исчезающе мал на частотах, близких к
нулю. Поэтому в выражении (7.5) можно
заменить нижний предел интегрирования
на
исчезающе мал на частотах, близких к
нулю. Поэтому в выражении (7.5) можно
заменить нижний предел интегрирования
на ,
не внося ощутимой погрешности, и записать
функцию корреляции в виде
,
не внося ощутимой погрешности, и записать
функцию корреляции в виде
 (7.6)
(7.6)
Особенно простой
функция корреляции узкополосного
процесса получается в случае, когда
спектр мощности
 симметричен относительно центральной
частоты
симметричен относительно центральной
частоты .
При этом
.
При этом ,
так что
,
так что
 (7.7)
(7.7)
Здесь коэффициент
 играет роль огибающей, которая изменяется
медленно по сравнению с множителем
играет роль огибающей, которая изменяется
медленно по сравнению с множителем .
Часто бывает удобным ввести нормированную
огибающую
.
Часто бывает удобным ввести нормированную
огибающую функции корреляции узкополосного
случайного процесса, определив её с
помощью равенства
функции корреляции узкополосного
случайного процесса, определив её с
помощью равенства .
.
Тогда
 (7.8)
(7.8)

Характерный вид функции корреляции (7.8) свидетельствует о том, что отдельные реализации узкополосного случайного процесса представляют собой квазигармонические колебания:
 , (7.9)
, (7.9)
у которых как
огибающая U(t),
так и начальная фаза
 являются случайными функциями, медленно
(в масштабе
являются случайными функциями, медленно
(в масштабе )
изменяющимися во времени.
)
изменяющимися во времени.
Представим реализацию (7.9) как сумму синфазной и квадратурной составляющих.
 (7.10)
(7.10)
Предположение о медленности синфазной A(t) и квадратурной B(t) амплитуд позволяет весьма просто записать выражение для реализации сопряжённого процесса, вынеся медленные множители за знак преобразования Гильберта:
 (7.11)
(7.11)
Отсюда получаем формулы для мгновенных значений реализации огибающей
 (7.12)
(7.12)
и начальной фазы
 (7.13)
(7.13)
Часто на практике
ставится задача нахождения совместной
плотности вероятности огибающей и
начальной фазы узкополосного случайного
процесса. При этом особенно удобно
воспользоваться методом, основанном
на переходе от узкополосного случайного
процесса к его синфазной и квадратурной
составляющим. Благодаря этому методу
мы можем вычислить двумерную плотность
вероятности
 .
Эта характеристика позволяет найти
одномерную плотность вероятности
огибающей:
.
Эта характеристика позволяет найти
одномерную плотность вероятности
огибающей:
 (7.14)
(7.14)
И плотность вероятности начальной фазы
 (7.15)
(7.15)
Мгновенные значения
амплитуды A(t)
и B(t)
образуют двумерный гауссов вектор, обе
составляющие которого независимы и
имеют одинаковые дисперсии
 .
Поэтому двумерная плотность вероятности.
.
Поэтому двумерная плотность вероятности.
 (7.16)
(7.16)
Теперь, чтобы
получить искомую плотность вероятности
 следует выполнить функциональное
преобразование, переводящее случайный
вектор {A,B}
в новую случайную совокупность
следует выполнить функциональное
преобразование, переводящее случайный
вектор {A,B}
в новую случайную совокупность
 ,
,
 (7.17)
(7.17)

Якобиан такого преобразования
 (7.18)
(7.18)
Поскольку в новых
переменных
 ,
искомая двумерная плотность вероятности:
,
искомая двумерная плотность вероятности:
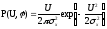 (7.19)
(7.19)
Теперь, используя формулы (7.15) и (7.19) можем найти плотность вероятности начальной фазы:

Введём замену
переменной

Тогда:
 (7.20)
(7.20)
Таким образом,
начальная фаза узкополосного случайного
процесса распределена равномерно на
отрезке

На основании формул (7.14) и (7.19) определим одномерную плотность вероятности огибающей
 (7.21)
(7.21)
Здесь так же
целесообразно перейти к безразмерной
переменной
 ,
относительно которой
,
относительно которой
 . (7.22)
. (7.22)
Плотность вероятности
мгновенных значений огибающей
узкополосного случайного процесса,
устанавливаемая выражением (7.21), (7.22)
известна под названием закона Рэлея.
Соответствующий график показывает, что
наиболее вероятны некоторые средние
(порядка
 )
значения огибающей. В то же время
маловероятно, чтобы огибающая принимала
значения как близкие к нулю, так и
значительно превосходящие среднеквадратичный
уровень
)
значения огибающей. В то же время
маловероятно, чтобы огибающая принимала
значения как близкие к нулю, так и
значительно превосходящие среднеквадратичный
уровень узкополосного процесса.
узкополосного процесса.

Проводя усреднение с помощью плотности вероятности (7.22) находим среднее значение огибающей и её дисперсию:
 (7.23)
(7.23)
 (7.24)
(7.24)
Располагая одномерной плотностью вероятности огибающей, можно решить ряд задач теории узкополосных случайных процессов, в частности, найти вероятность превышения огибающей некоторого заданного уровня.
Случайные величины, распределенные по закону Рэлея, встречаются во многих задачах. Исследуем огибающую суммы гармонического сигнала и узкополосного нормального шума. Часто бывает необходимо определить статистические свойства сигнала, наблюдаемого на выходе некоторого частотно-избирательного устройства, например, резонансного усилителя.
Будем считать, что
помимо флуктуационного гауссова шума
с центральной частотой
 ,
равной резонансной частоте усилителя,
на выходе присутствует также
детерминированный гармонический сигнал
,
равной резонансной частоте усилителя,
на выходе присутствует также
детерминированный гармонический сигнал с известной амплитудой
с известной амплитудой .
.
Простейшей задачей
является нахождение одномерной плотности
вероятности огибающей суммарного
колебания. Считая, что полезный сигнал
 ,
в то время как шум
,
в то время как шум ,
запишем выражение реализации суммарного
процессаX(t)
,
запишем выражение реализации суммарного
процессаX(t)
 .
Данный случайный процесс узкополосен,
поэтому его реализация может быть
выражена посредством медленно меняющихся
огибающейU(t)
и начальной фазы
.
Данный случайный процесс узкополосен,
поэтому его реализация может быть
выражена посредством медленно меняющихся
огибающейU(t)
и начальной фазы
 :
:
 .
Очевидно, между парами
.
Очевидно, между парами
 имеется связь:
имеется связь:
 (7.25)
(7.25)
Легко проверить, что якобиан D этого преобразования равен U. Тогда, поскольку двумерная плотность вероятности:

В новых переменных имеем.
 (7.26)
(7.26)
Теперь чтобы получить одномерную плотность вероятности огибающей, следует проинтегрировать правую часть формулы (7.26) по угловой координате в результате чего находим:
 (7.27)
(7.27)
Данная формула
выражает закон, получивший название
закона Райса. Отметим, что при
 ,
т.е. в отсутствие детерминированного
сигнала, закон Райса переходит в закон
Рэлея.
,
т.е. в отсутствие детерминированного
сигнала, закон Райса переходит в закон
Рэлея.
На рисунке
представлены графики плотности
вероятности случайной величины,
распределённой по закону Райса при
различных отношениях

 Отметим,
что если амплитуда детерминированного
сигнала значительно превышает
среднеквадратический уровень шума,
т.е.
Отметим,
что если амплитуда детерминированного
сигнала значительно превышает
среднеквадратический уровень шума,
т.е.
 >>1
то при
>>1
то при
 можно воспользоваться асимптотическим
представлением модифицированных функций
Бесселя с большим аргументом:
можно воспользоваться асимптотическим
представлением модифицированных функций
Бесселя с большим аргументом:

Подставив это выражение в (7.27), имеем
 (7.28)
(7.28)
Т.е. огибающая
результирующего сигнала распределена
в этом случае приближённо нормально с
дисперсией
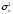 и математическим ожиданием
и математическим ожиданием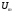 .
Практически считают, что уже при
.
Практически считают, что уже при огибающая результирующего сигнала
нормализуется.
огибающая результирующего сигнала
нормализуется.
