2. Чисельне рішення задачі Коши для звичайного диференційного рівняння першого порядку

Багато наукових і технічних задач призводять до рішення диференційних рівнянь. Рідко зустрічаються диференційні рівняння, які можна проінтегрувати аналітичними методами, знайшовши точне рішення. Особливе значення, таким чином, мають наближені методи вирішення диференційних рівнянь. До відомих чисельних методів належать метод Ейлера і метод Рунге-Кутта.

Задане диференційне рівняння першого порядку виду , що задовольняє початковим умовамНеобхідно знайти рішення диференційного рівняння на відрізку.

Метод Ейлера для задачі Коши звичайного диференційного рівняння першого порядку полягає в тому, що рішення рівняння обчислюється за формулою: , де.

У методі Рунге-Кутта четвертого порядку рішення задачі Коши звичайного диференційного рівняння першого порядку обчислюється за формулою: , де,,,,.

Приклад 1. Знайти наближене чисельне рішення диференційного рівняння , що задовольняє початковим умовамза допомогою методів Ейлера і Рунге-Кутта.

Задане рівняння є лінійним неоднорідним рівнянням першого порядку. Графіки рішення на інтерваліз кроком, де початкове і кінцеве значеннях дорівнюють ,– кількість точок на інтервалі зміних, показані на рис. 39.

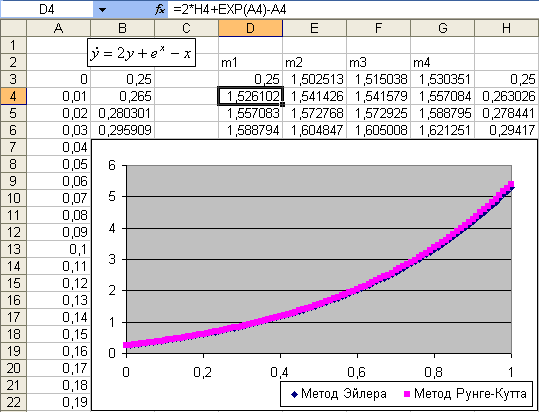
Рис. 39. Чисельне рішення диференційного рівняння ,.

Для метода Ейлера в клітинці В3 (рис. 39) наведене початкове значення , а в клітинціВ4 поточне значення y обчислюється за формулою Ейлера , де,- крок пох, а значення беруться з рядка 3:=B3+0,01*(2*B3+EXP(A3)-A3). Формула у клітинці В4 копіюється на весь стовпець.

Для метода Рунге-Кутта в клітинці Н3 (рис. 39) наведене початкове значення , а в клітинціD3 значення дорівнює значеннюy: =Н3. Значення в клітинціЕ3 обчислюється за формулою =2*(H3+D3*0,005)+EXP(A3+0,005)-(A3+0,005), де ,- крок пох, а значення беруться з клітинокА3 і Н3 відповідно. Аналогічно обчислюється коефіцієнт у клітинціF3: =2*(H3+E3*0,005)+EXP(A3+0,005)-(A3+0,005), та коефіцієнт у клітинціG3 з використанням кроку :=2*(H3+F3*0,01)+EXP(A3+0,01)-(A3+0,01).

Поточне значення у знаходиться в клітинці Н4 за формулою Рунге-Кутта , де- крок пох, а значення беруться з попереднього рядка 3:=H3+(D3+2*E3+2*F3+G3)*0,01/6.

Друге значення коефіцієнта в клітинціD4 обчислюється за формулою :=2*H4+EXP(A4)-A4, де значення беруться з клітинокА4 і Н4 відповідно. Формули у клітинках D4, E3, F3, G3, H4 копіюються на всі стовпці.

Графіки чисельного рішення (див. рис. 39) диференційного рівняння,, отримані методами Ейлера та Рунге-Кутта четвертого порядку, майже співпадають на інтервалізавдяки обраному невеликому кроку пох.

Приклад 2. Знайти наближене чисельне рішення диференційного рівняння , або, що задовольняє початковим умовамза допомогою методів Ейлера і Рунге-Кутта. Графіки рішенняна інтерваліз крокомпоказані на рис. 40.

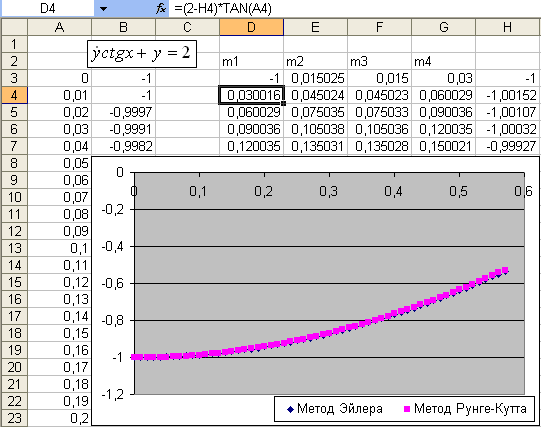
Рис. 40. Чисельне рішення диференційного рівняння ,.

Для метода Ейлера в клітинці В3 (рис. 40) наведене початкове значення , а в клітинціВ4 поточне значення y обчислюється за формулою Ейлера , де,- крок пох, а значення беруться з рядка 3:=B3+0,01*(2-B3)*TAN(A3). Формула у клітинці В4 копіюється на весь стовпець.

Для метода Рунге-Кутта в клітинці Н3 (рис. 40) наведене початкове значення , а в клітинціD3 значення дорівнює значеннюy: =Н3. Значення в клітинціЕ3 обчислюється за формулою =(2-H3-D3*0,005)*TAN(A3+0,005), де ,- крок пох, а значення беруться з клітинокА3 і Н3 відповідно. Аналогічно обчислюється коефіцієнт у клітинціF3: =(2-H3-E3*0,005)*TAN(A3+0,005), та коефіцієнт у клітинціG3 з використанням кроку :=(2-H3-F3*0,01)*TAN(A3+0,01).

Поточне значення у знаходиться в клітинці Н4 за формулою Рунге-Кутта , де- крок пох, а значення беруться з попереднього рядка 3:=H3+(D3+2*E3+2*F3+G3)*0,01/6.

Друге значення коефіцієнта в клітинціD4 обчислюється за формулою :=(2-H4)*TAN(A4), де значення беруться з клітинокА4 і Н4 відповідно. Формули у клітинках D4, E3, F3, G3, H4 копіюються на всі стовпці.

Графіки чисельного рішення (див. рис. 40) диференційного рівняння,, отримані методами Ейлера та Рунге-Кутта четвертого порядку, майже співпадають на інтервалізавдяки обраному невеликому кроку пох.