Вступ

В час, коли наше життя не можна уявити без використання комп’ютера, автоматизація розрахунків має велике значення. Існує безліч програмних продуктів для вирішення інженерних задач. Серед них можна виділити додаток MS Excel, який вивчався в курсі «Інформатика». Він дуже простий у використанні, має широкий набір вмонтованих утиліт та функцій, які допомагають розв’язати різноманітні задачі, в тому числі виконувати складні обчислення, будувати графіки різноманітних кривих, поверхонь і таке інше. В методичних вказівках розглядаються питання побудови графіків різноманітних кривих, поверхонь, наближеного рішення рівнянь та систем, обчислення похідних та інтегралів, задачі інтерполяції та апроксимації. В методичних вказівках надані скорочені теоретичні відомості та практичні рекомендації по рішенню кожного класу задач.

1. Побудова плоских кривих

Криві на площині у декартових координатах

Крива на площині у декартових координатах — це множина точок, координати яких пов’язані відношеннямабо; перший вираз задає криву явно, останній – неявно. Крива, задана рівнянням, має назвугладкої, якщо функція диференційована на інтервалі . В кожній точцігладкої кривої можливо провести дотичну, рівняння якоїРівняннянормалі в тій самій точці має вигляд .

Приклад 1. Побудова кривої у декартових координатах.

Графік гіперболічного косинусу побудовано на інтервалідля кількості точок 100. Формула для прирощення пов ячейці F2:=(D2-C2)/E2. Перше значення в ячейці А2 дорівнює:=C2. В ячейку А3 вводимо формулу: =A2+$F$2, де посилання на ячейку з прирощенням по дається в абсолютній адресації. Далі формула з ячейки А3 копіюється черезАвтозаполнитель на інші ячейки стовпця А, останній дорівнює. В ячейку В2 вводиться формула для обчислення гіперболічного косинусу:і копіюється на інші ячейки стовпця В. Для побудови графіка використовується тип діаграмиТочечная (Рис. 1).

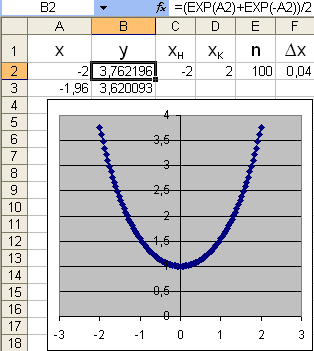
Рис. 1. Графік гіперболічного косинусу .

Криві, задані параметрично

Рівняння , що встановлюють залежність декартових координатточки від значення параметру , визначають криву, задану у параметричній формі. Оскільки похідна функції що задана параметрично рівняннями , у точці, яка не є особливою точкою кривої, обчислюється за формулою , то рівняння дотичної і нормалі до кривої через точку, мають вигляд, відповідно:

Приклад 2. Побудова кривої, заданої параметрично.

Графік астроїди побудовано на інтервалідля кількості точок 100 в декартових координатах(рис. 2).

Рис. 2. Графік астроїди .

Криві у полярних координатах

Певні криві на площині зручно описувати як функції радіуса-вектора і полярного кута— у полярних координатах. Так, рівняння одиничного кола у полярних координатах має вигляд. Рівняння кривої вполярних координатах звичайно має вигляд . Декартові координати точкина площині пов’язані з полярними координатамивиразамиЯкщо відомі декартові координати точки, то її полярні координати визначаються за формулами, . Кутовий коефіцієнт дотичної до графіку функції, заданої рівнянням , в точцідорівнює, а декартові координати точки дорівнюють і.

Приклад 3. Побудова кривої, заданої у полярних координатах.

Графік функції декартів лист ,a=2 побудовано на інтервалі для кількості точок 100 в декартових координатах(рис. 3).

Рис. 3. Графік функції декартів лист .

Графіки деяких кривих

Конхоїда Никомеда ― конхоїда прямої алгебраїчна крива 4-го порядку на площині. Конхоїда має дві вітки, пряма конхоїди є асимптотою обох віток.

У полярних координатах, якщо вмістити початок координат вище прямої на відстань a, рівняння конхоїди має вигляд (див. рис. 4) або - повернута на π/2 проти годинникової стрілки.

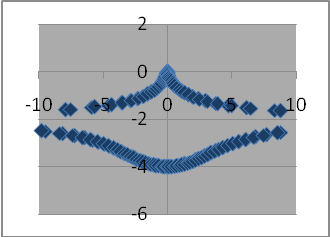
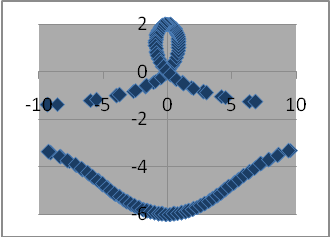
Рис. 4. Три конхоїди прямої зі спільним центром :

Внутрішня , середняі зовнішня.

Равлик Паскаля ― алгебраїчна крива 4-го порядку на площині, конхоїда кола. Названа за ім’ям Етьєна Паскаля, який її вперше розглянув. Рівняння у полярних координатах має вигляд:

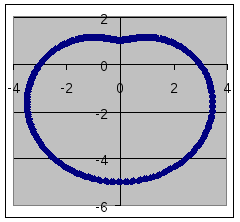
Рис. 5. Три равлики Паскаля – конхоїди кола: зовнішній , середній (кардіоїда) і внутрішній .

Кардіоїда ― лінія на площині, що описується фіксованою точкою кола, що котиться по нерухомому колу того ж радіусу. Отримала свою назву через схожість своїх контурів зі стилізованим зображенням серця. Кардіоїда є окремим випадком равлика Паскаля і синусоїдальної спіралі. Рівняння у полярних координатах має вигляд:

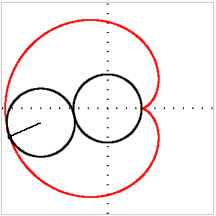
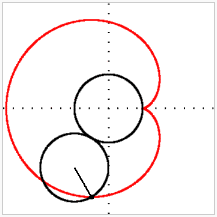
Рис. 6. Побудова кардіоїди.

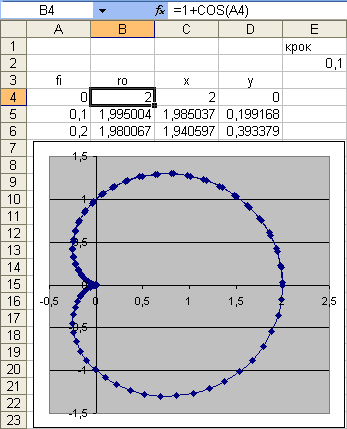
Рис. 7. Графік кардіоїди

Архімедова спіраль — спіраль, крива на площині, траєкторія точки M (див. рис. 6), що рівномірно рухається вздовж променя OV з початком у точці O, при цьому сам промінь OV рівномірно обертається навколо O. Тобто відстань ρ = OM пропорційна куту повороту φ променя OV.

Рівняння Архімедової спіралі у полярній системі координат має вигляд: абодеk — зсув точки M по променю r при повороті на кут в один радіан, число a – крок спіралі.

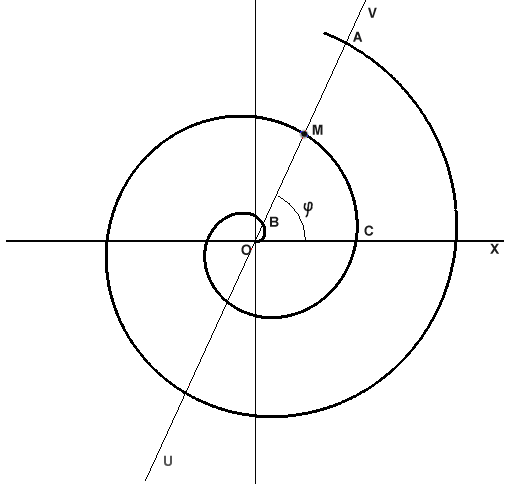
Рис. 8. Побудова Архімедової спіралі.

Права і ліва вітка спіралі описуються одним рівнянням. Додатнім значенням φ відповідає права спіраль, від’ємним - ліва спіраль.

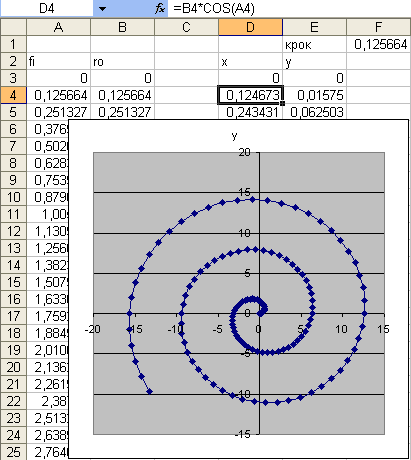
Рис. 9. Графік Архімедової спіралі

Астроїда - крива на площині, що описується точкою кола радіуса r, яка котиться внутрішньою стороною кола радіуса R = 4r. Астроїда — це гіпоциклоїда з модулем m = 4. Параметричні рівняння астроїди: x = Rcos³t; y=Rsin³t.

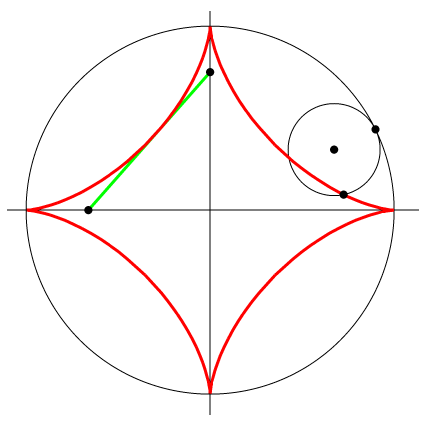
Рис. 10. Побудова астроїди.