§5. Смешанное произведение векторов

Определение.

Пусть даны три вектора ,и. Смешанным произведением векторов,иназывается число, обозначаемоеи определяемое равенством

.

Свойства смешанного произведения векторов.

Свойство 1.

Если

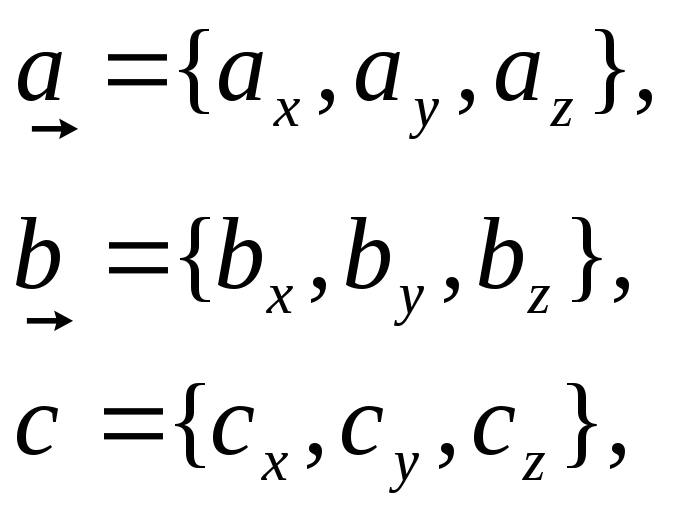
То

.

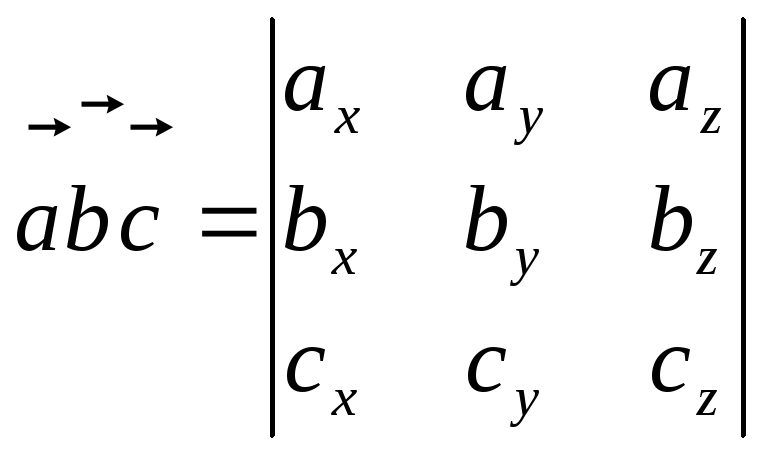Это свойство смешанного произведения следует непосредственно из свойств векторного и скалярного произведения векторов:

.

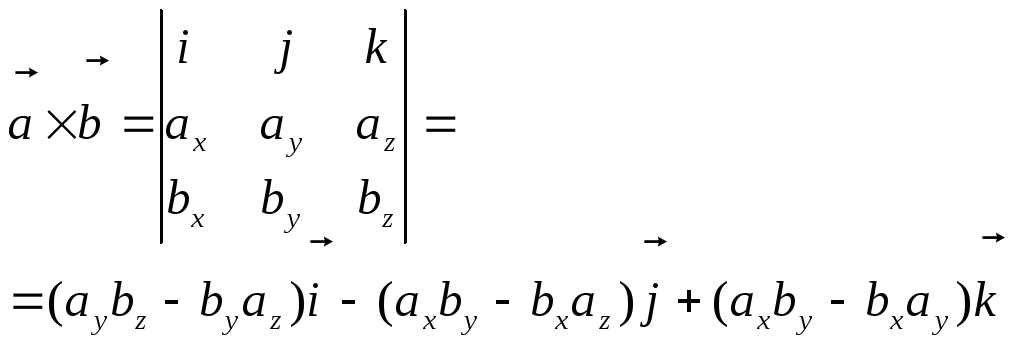
Следовательно

.

С другой стороны, если разложить определитель

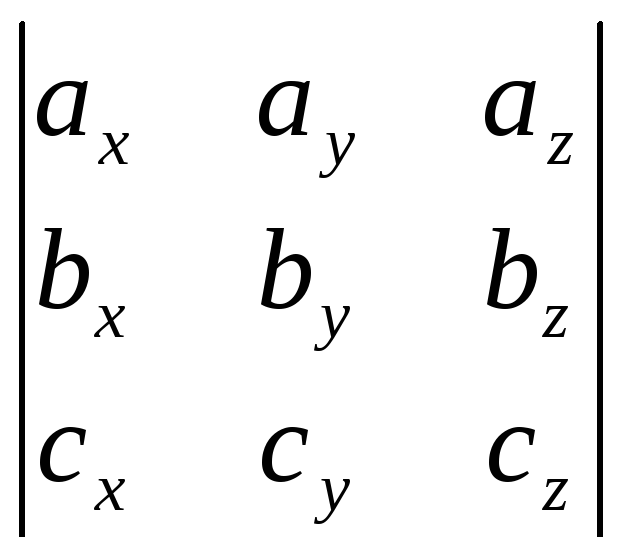
по третьей строке, то получим

.

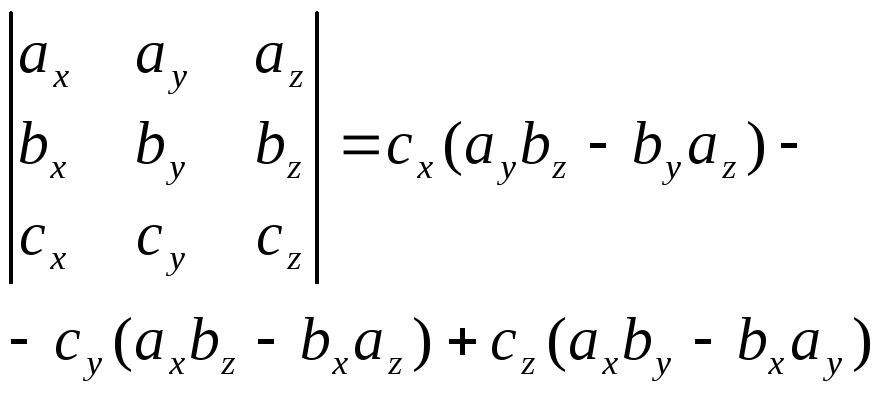Таким образом, смешанное произведение можно представить указанным определителем.

Свойство 2.

.

Это свойство следует непосредственно из выражений векторного и скалярного произведений через координаты векторов и доказывается так же как и свойство 1.

Свойство 3.

,

т. е. при перестановке двух любых сомножителей смешанное произведение меняет знак. Это свойство проверяется непосредственно с помощью свойства 1.

Свойство 4.

Для того, чтобы векторы ,ибыли компланарны необходимо и достаточно, чтобы выполнялось равенство

.

Докажем это свойство.

Пусть векторы ,иненулевые и лежат в одной плоскости, т.е. компланарны. Покажем, что. В самом деле, векторперпендикулярен плоскости, в которой лежат векторыи, значит перпендикулярен вектору, так как он также лежит в этой плоскости. Следовательно. Обратно, пусть. Если,иненулевые векторы и, то векторперпендикулярен. Кроме того, векторперпендикулярен векторуи векторперпендикулярен вектору. Следовательно, все три вектора,иперпендикулярны одному и тому же векторуи значит лежат в одной и той же плоскости (будучи отложенными от общей точки).

Из последнего свойства в частности следует, что если какие-то два из тройки векторов ,иколлинеарны, то, так как в этом случае векторы,икомпланарны.

Введем понятие параллелепипеда, построенного на тройке векторов.

Определение.

Пусть ненулевые векторы ,инекомпланарны. Отложим их от общей точки. Обозначим,,плоскости, в которых лежат пары векторов,и, соответственно. Через конец векторапроведем плоскость, параллельную, через конец векторапроведем плоскость, параллельную плоскости, через конец векторапроведем плоскость, параллельную плоскости. Тогда,,,и построенные

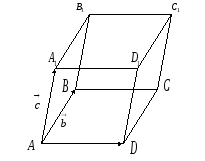
Рис. 30.

плоскости ограничивают параллелепипед . Этот параллелепипед называется параллелепипедом, построенном на векторах,и. Теперь сформулируем свойство 5 смешанного произведения.

Свойство 5.

Если тройка векторов правая, то

,

если же тройка левая, то

,

где - объем параллелепипеда, построенного на векторах,и. Докажем это свойство.

Пусть-правая тройка векторов. По определению

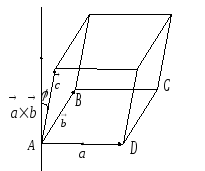
Рис. 31.

.

где - угол между векторамии. Построим на векторах,ипараллелепипед (Рис. 31). Объем этого параллелепипеда равен

,

где - площадь основания,- высота параллелепипеда. Так какпараллелограмм, то

.

Высота в случае, когдаправая тройка, как видно из рисунка , равна

.

Следовательно, учитывая, что

,

получаем

,

где - угол между векторамии. Таким образом,

.

Пусть теперь - левая тройка векторов. Построим параллелепипед на векторах,и. Как видно

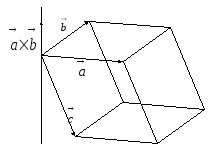
Рис. 32.

из рисунка 32, в этом случае

,

где - угол между векторамии, причем уголв этом случае тупой и значитотрицателен. Следовательно, в случае левой тройки векторов

.

Замечание.

Независимо от того, является ли тройка векторов правой или левой, объем параллелограмма, построенного на этих векторах, равен

.

В самом деле, если - правая тройканеотрицательное число и значит

.

В случае, когда левая тройка, числоотрицательно и. следовательно,

.

Пусть имеется тройка ненулевых некомпланарных векторов ,и. Отложим их от общей точки. Если

Рис. 33.

Концы векторов соединить отрезками, как это показано на рисунке 33, то получим треугольную пирамиду. Эта пирамида называется пирамидой, построенной на векторах,и.

В элементарной геометрии доказывается, что объем этой пирамиды равен одной шестой объема параллелепипеда, построенного на векторах,и. Отсюда следует, что объем пирамиды равен

.

Рассмотрим пример на свойство 4.

Пример.

Доказать, что точки ,,илежат в одной плоскости.

Решение.

Точки лежат в одной плоскости тогда и только тогда, когда векторыкомпланарны. Покажем, что выполнено условие компланарности (свойство 4)

.

Найдем координаты векторов

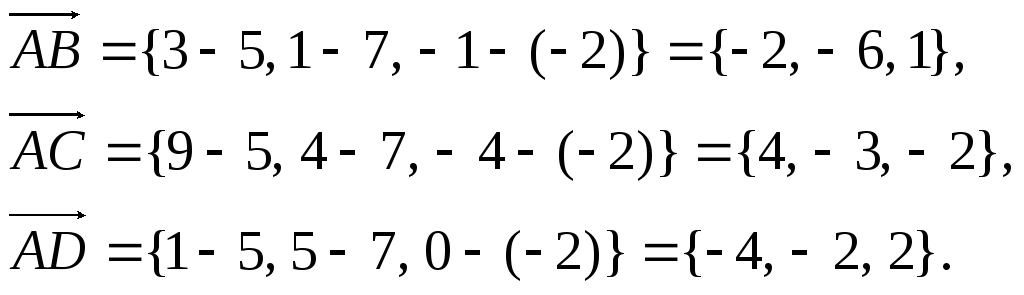
Тогда, согласно свойству 1

.

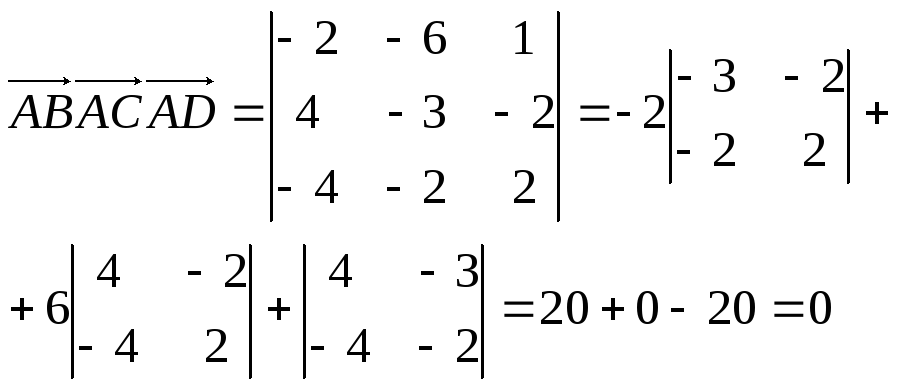Следовательно, векторы коллинеарны (лежат в одной плоскости), а значит точкилежат в одной плоскости.