Глава 3. Плоскость в пространстве.

§1. Уравнение плоскости в пространстве

Определение.

Уравнением с тремя неизвестными называется выражение вида

например,

Определение.

Решением уравнения называется любая упорядоченная тройка чиселтакая, что при подстановке вместоичисели, соответственно, получается верное числовое равенство. Например, тройка чиселявляется решением уравнения

так как при подстановке этих чисел в уравнение получается верное числовое равенство.

Далее будем всегда предполагать, что в пространстве задана Декартова система координат. Тем самым, между тройками чисел и точками пространства установлено взаимно однозначное соответствие.

Определение.

Уравнение вида называется уравнением поверхности в пространстве если выполнено следующее:

1) Пусть точка лежит на поверхности. Тогда тройка чиселявляется решением уравнения.

2) Пусть тройка чисел является решением уравнения, тогда точкалежит на рассматриваемой поверхности.

Ниже будем рассматривать один из видов поверхностей, а именно плоскость. При рассмотрении плоскости будем опираться на понятия и утверждения, рассматриваемые в элементарной (школьной) геометрии.

Из элементарной геометрии известно, что существует единственная плоскость, проходящая через заданную точку и перпендикулярная заданному вектору. Выведем уравнение этой плоскости. Утверждение сформулируем в виде теоремы.

Теорема.

Уравнение плоскости, проходящей через заданную точку и перпендикулярной заданному вектору(нормаль к плоскости) имеет вид

.

Доказательство.

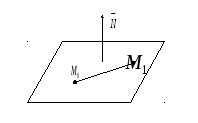
Рис. 44.

Пусть плоскость проходит через заданную точку и перпендикулярна заданному вектору. Возьмем на плоскости произвольную точку, отличную от точки. Тогда из элементарной геометрии следует, что векторперпендикулярен вектору. Следовательно,

.

Поскольку

,

получаем, что равенство, выражающее скалярное произведение в координатной форме

является верным числовым равенством. А это означает, что тройка чисел является решением уравнения

.

Непосредственной подстановкой в уравнение легко убедиться, что тройка чисел также является решением этого уравнения. Таким образом, если точка лежит на плоскости, то ее координаты образуют решение рассматриваемого уравнения.

Докажем теперь, что если тройка чисел есть решение рассматриваемого уравнения, то точка, координаты которой есть эти числа, лежит на плоскости.

Пусть тройка чисел есть решение уравнения

,

то есть

есть верное числовое равенство. Докажем, что точка

принадлежит плоскости. Доказательство проведем от противного. Допустим, что точкане лежит на плоскости (Рис. 45)

Рис. 45.

Из элементарной геометрии следует, что вектор

не перпендикулярен вектору . Тогда равенство

не является верным числовым равенством. Или соответствующее равенство для координат

не является верным числовым равенством. Но это противоречит сделанному предположению о том, что тройка чисел есть решение уравнения

,

и значит равенство

есть верное числовое равенство. Следовательно, предположение о том, что точка не лежит на плоскости не верно. Следовательно, точкалежит на плоскости. Теорема доказана.

Пример.

Записать уравнение плоскости, проходящей через точку и перпендикулярной вектору.

Решение.

Как показано выше, уравнение имеет вид

или

.

Если в уравнении

раскрыть скобки, то получим уравнение вида

.

Обозначим

.

Тогда уравнение примет вид

.

Таким образом, уравнение любой плоскости можно записать в виде

.

При этом вектор нормали к плоскости равен . Уравнение плоскости, записанное в таком виде, называется общим уравнением плоскости. Можно показать, что уравнение вида

,

где хотя бы одно из чисел отлично от нуля, есть уравнение какой-то плоскости.

Как известно из элементарной геометрии, через три точки, не лежащие на одной прямой, можно провести плоскость и при том только одну. В связи с этим в общем виде рассмотрим следующую задачу. Записать уравнение плоскости, проходящей через три точки

,

не лежащие на одной прямой.

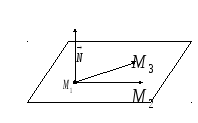
Рис. 46.

Векторы илежат в плоскостии не коллинеарны так как точкине лежат на одной прямой. Тогда вектор, будучи перпендикулярным векторам, будет перпендикулярен плоскости. Следовательно, вектор

можно взять в качестве нормали к плоскости. Тогда поставленная задача сводится к решению рассмотренной выше задачи: записать уравнение плоскости, проходящей через точкуи перпендикулярной вектору. Уравнение этой плоскости можно записать в виде

.

Так как , то левая часть уравнения принимает вид смешанного произведения векторов

.

Учитывая, что

и что смешанное произведение можно записать в виде определителя, получим искомое уравнение плоскости в виде

.

Если разложить этот определитель по строке или столбцу, то окончательно уравнение примет вид общего уравнения плоскости.

Пример.

Записать уравнение плоскости, проходящей через точки .

Решение.

Выше получено, что уравнение имеет вид

.

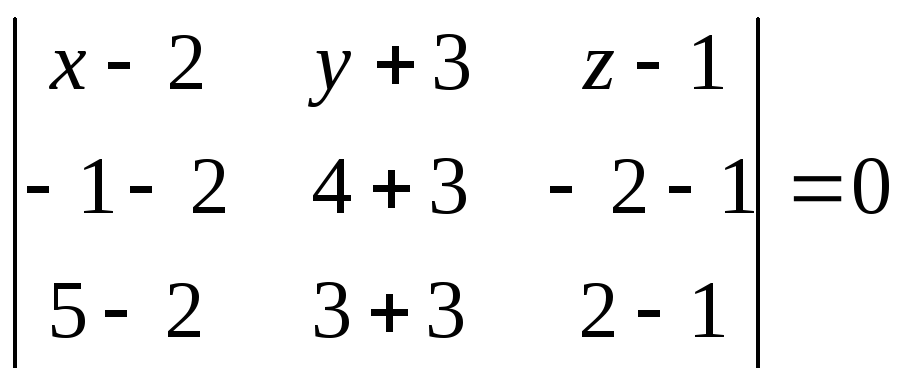Или

.

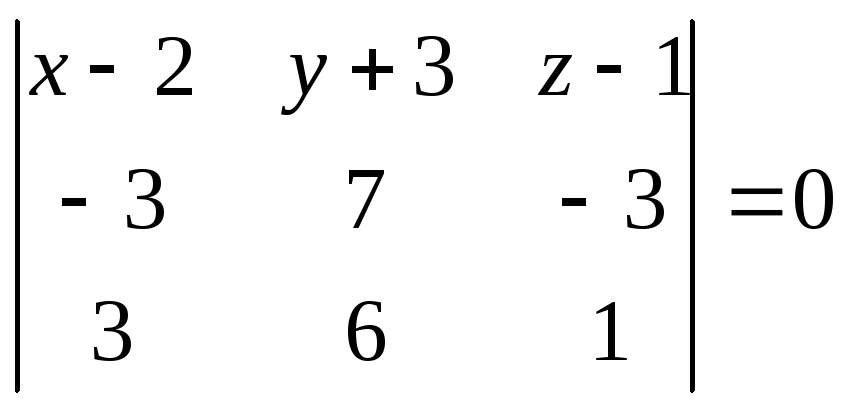Разлагая определитель, например по первой строке, получим искомое уравнение плоскости

.