
- •Глава 1. Векторная алгебра
- •§1. Основные понятия векторной алгебры
- •§2. Проекция вектора на ось.
- •§3. Координаты вектора
- •§4. Скалярное произведение векторов
- •§5. Векторное произведение векторов
- •§5. Смешанное произведение векторов
- •Глава 2. Прямая на плоскости
- •§1. Уравнение прямой на плоскости, проходящей через заданную точку и перпендикулярной заданному вектору
- •§2. Параметрические и канонические уравнения прямой на плоскости
- •§3. Взаимное расположение прямых на плоскости
- •§4. Расстояние от точки до прямой
- •§5. Уравнение прямой с угловым коэффициентом
- •Глава 3. Плоскость в пространстве.
- •§1. Уравнение плоскости в пространстве
- •§ 2. Взаимное расположение плоскостей в пространстве
- •Глава 4. Прямая в пространстве
- •§1. Общие уравнения прямой в пространстве
- •§2. Параметрические и канонические уравнения прямой в пространстве
- •§ 3. Переход от одного вида уравнения прямой к другому виду
- •§4. Взаимное расположение прямых в пространстве. Угол между прямыми.
- •Глава 5. Взаимное расположение прямой и плоскости
§ 2. Взаимное расположение плоскостей в пространстве
Две плоскости могут совпадать, быть параллельными или пересекаться по прямой. Ниже рассматривается вопрос о том, как по уравнениям плоскостей определить их взаимное расположение.
Пусть две плоскости
![]() и
и![]() заданы своими уравнениями
заданы своими уравнениями
![]()
![]()
![]() и
и![]() - нормали плоскостей
- нормали плоскостей![]() и
и![]() ,
соответственно.
,
соответственно.
Из элементарной геометрии следует,
что плоскости совпадают или параллельны
тогда и только тогда, когда их нормали
коллинеарны, то есть существует число
![]() такое, что справедливо равенство
такое, что справедливо равенство
![]() .
.
Если плоскости совпадают, то все точки у них общие. Поэтому любое решение уравнения одной плоскости будет также решением уравнения другой плоскости. Если это не выполняется, то плоскости параллельны.
Пример.
Даны две плоскости, заданные уравнениями
![]()
Определить взаимное расположение плоскостей.
Решение.
Векторы нормалей равны
![]() .
.
Так как
![]() ,
,
то нормали коллинеарны и значит плоскости
либо совпадают, либо параллельны. Легко
проверить, что тройка чисел
![]() является решением первого уравнения и
не является решением второго. Следовательно,
плоскости параллельны.
является решением первого уравнения и
не является решением второго. Следовательно,
плоскости параллельны.
Если векторы
![]() и
и![]() не коллинеарны, то есть условие
не коллинеарны, то есть условие![]() не выполняется ни при каком
не выполняется ни при каком![]() ,
то плоскости пересекаются по прямой. В
этом случае можно поставить вопрос об
угле, под которым они пересекаются.
Пересекающиеся плоскости образуют
двугранные углы, мерой которых являются
мера соответствующего линейного угла.
Так же как и в случае пересекающихся
прямых на плоскости, пересекающиеся
плоскости (если они не перпендикулярны)
образуют острый и тупой двугранные
углы, который в сумме составляют
,
то плоскости пересекаются по прямой. В
этом случае можно поставить вопрос об
угле, под которым они пересекаются.
Пересекающиеся плоскости образуют
двугранные углы, мерой которых являются
мера соответствующего линейного угла.
Так же как и в случае пересекающихся
прямых на плоскости, пересекающиеся
плоскости (если они не перпендикулярны)
образуют острый и тупой двугранные
углы, который в сумме составляют![]() .
Из элементарной геометрии следует, что
линейные углы равны углам между векторами
нормалей к плоскостям. При этом, если
угол между нормалями острый, то этот
угол равен острому двугранному углу (и
соответствующему ему линейному углу),
а если тупой, то он равен тупому двугранному
углу, образованному плоскостями. Как
известно, косинус угла
.
Из элементарной геометрии следует, что
линейные углы равны углам между векторами
нормалей к плоскостям. При этом, если
угол между нормалями острый, то этот
угол равен острому двугранному углу (и
соответствующему ему линейному углу),
а если тупой, то он равен тупому двугранному
углу, образованному плоскостями. Как
известно, косинус угла![]() между
нормалями можно найти по формуле
между
нормалями можно найти по формуле
![]() .
.
Если получаем, что
![]() ,
то угол
,
то угол![]() - острый угол, равный острому двугранному
углу между плоскостями. Если
- острый угол, равный острому двугранному
углу между плоскостями. Если![]() ,
то
,
то![]() равен тупому двугранному углу между
плоскостями.
равен тупому двугранному углу между
плоскостями.
Как и в случае пересекающихся прямых на плоскости, если поставить задачей найти острый угол между плоскостями, то можно получить следующее выражение для острого угла
![]() .
.
Пример.
Даны плоскости, заданные уравнениями
![]()
Найти острый угол между плоскостями.
Решение.
Векторы нормалей равны
![]()
Следовательно, косинус острого угла
![]() равен
равен
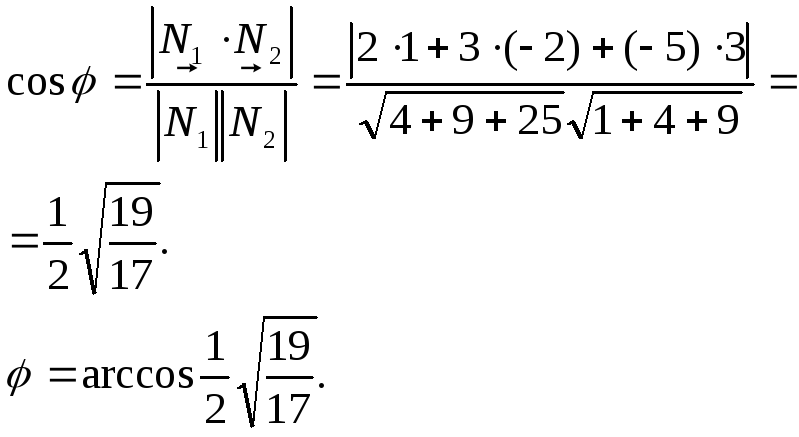
Наконец, рассмотрим условие перпендикулярности плоскостей. Как следует из элементарной геометрии, две плоскости будут взаимно перпендикулярными тогда и только тогда, когда взаимно перпендикулярны их нормали, то есть их скалярное произведение равно нулю
![]()
Пример.
Доказать, что плоскости
![]()
взаимно перпендикулярны.
Решение.
Векторы нормалей равны
![]()
Находим скалярное произведение
![]()
Следовательно, нормали перпендикулярны, а значит и плоскости взаимно перпендикулярны.
