
- •Глава 1. Векторная алгебра
- •§1. Основные понятия векторной алгебры
- •§2. Проекция вектора на ось.
- •§3. Координаты вектора
- •§4. Скалярное произведение векторов
- •§5. Векторное произведение векторов
- •§5. Смешанное произведение векторов
- •Глава 2. Прямая на плоскости
- •§1. Уравнение прямой на плоскости, проходящей через заданную точку и перпендикулярной заданному вектору
- •§2. Параметрические и канонические уравнения прямой на плоскости
- •§3. Взаимное расположение прямых на плоскости
- •§4. Расстояние от точки до прямой
- •§5. Уравнение прямой с угловым коэффициентом
- •Глава 3. Плоскость в пространстве.
- •§1. Уравнение плоскости в пространстве
- •§ 2. Взаимное расположение плоскостей в пространстве
- •Глава 4. Прямая в пространстве
- •§1. Общие уравнения прямой в пространстве
- •§2. Параметрические и канонические уравнения прямой в пространстве
- •§ 3. Переход от одного вида уравнения прямой к другому виду
- •§4. Взаимное расположение прямых в пространстве. Угол между прямыми.
- •Глава 5. Взаимное расположение прямой и плоскости
§4. Скалярное произведение векторов
Определение.
Пусть даны два ненулевых вектора
![]() и
и![]() .
Скалярным произведением векторов
.
Скалярным произведением векторов![]() и
и![]() называется
число, обозначаемое
называется
число, обозначаемое![]() и
равное
и
равное
![]() ,
,
где
![]() -
угол между векторами
-
угол между векторами![]() и
и![]() .
Если хотя бы один из векторов нулевой,
то полагаем, что
.
Если хотя бы один из векторов нулевой,
то полагаем, что![]() .
При обозначении скалярного произведения
точка часто опускается.
.
При обозначении скалярного произведения
точка часто опускается.
Свойства скалярного произведения сформулируем в виде теоремы.
Теорема.
Свойства скалярного произведения.
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5) Если
![]() ,
,![]() и
и![]() - орты осей координат, то
- орты осей координат, то
![]() .
.
6) Если
![]() ,
,
![]() ,
,
то
![]() .
.
7) Векторы
![]() и
и![]() взаимно
перпендикулярны тогда и только тогда,
когда
взаимно
перпендикулярны тогда и только тогда,
когда
![]()
Доказательство.
Свойства 1, 2, 3, 5 следуют непосредственно из определения скалярного произведения. Свойство 4 следует из теоремы 10 о проекции суммы векторов. Действительно,
![]() .
.
Далее из свойств 4 и 5 получаем свойство 6. Имеем
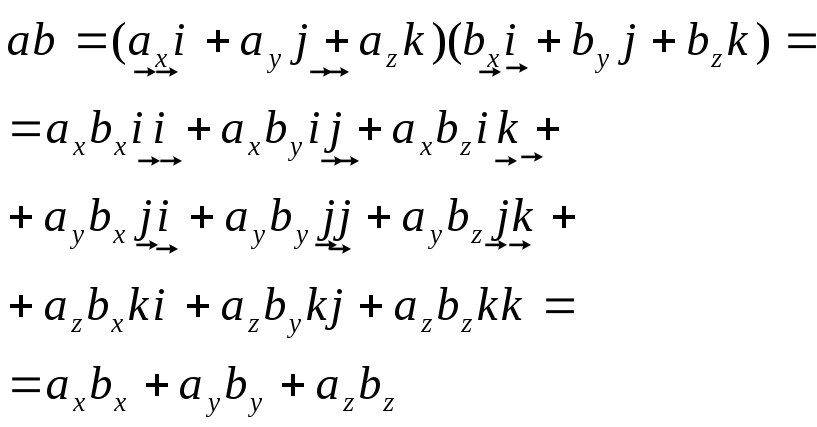
В последних равенствах учтено, что
![]() ,
,
а
![]() .
.
Рассмотрим свойство 7. Если векторы
![]() и
и![]() взаимно
перпендикулярны, то
взаимно
перпендикулярны, то
![]() .
.
Если же
![]() ,
,
где
![]() -
угол между векторами и
-
угол между векторами и![]() и
и![]() ненулевые
векторы, то
ненулевые
векторы, то![]() .
Отсюда
.
Отсюда![]() и значит векторы
и значит векторы![]() и
и![]() взаимно перпендикулярны. Таким образом,
чтобы ненулевые векторы
взаимно перпендикулярны. Таким образом,
чтобы ненулевые векторы![]() и
и![]() были
взаимно перпендикулярны необходимо и
достаточно, чтобы выполнялось равенство
были
взаимно перпендикулярны необходимо и
достаточно, чтобы выполнялось равенство![]() .
.
Из определения скалярного
произведения следует, что если
![]() и
и![]() ненулевые векторы, то
ненулевые векторы, то
![]() .
.
В свою очередь, зная координаты векторов, можно найти скалярное произведение и длины векторов. Таким образом, зная координаты векторов, можно найти косинус угла между векторами, а зная косинус можно найти и сам угол.
Пример.
![]() .
.
Найти угол между векторами.
Решение.
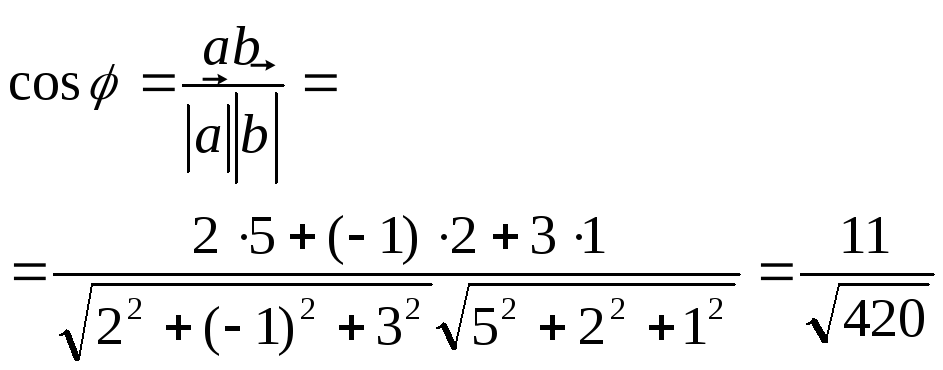
Отсюда
![]()
![]() .
.
§5. Векторное произведение векторов
Введем понятие определителя. С помощью определителя удобно записывать одно из свойств векторного произведения векторов. Кроме того, понятие определителя будет применяться при рассмотрении смешанного произведения векторов.
Матрицей размером
![]() называется таблица из чисел вида
называется таблица из чисел вида
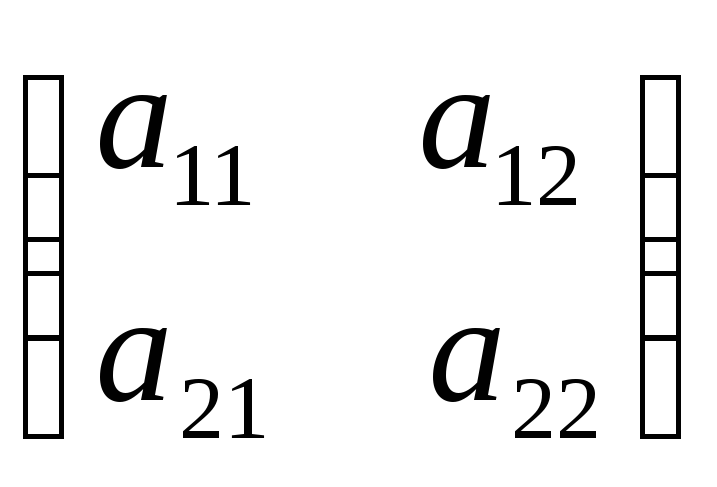
Определителем этой матрицы называется число, обозначаемое в виде
![]()
и вычисляемое по формуле
![]() .
.
Матрицей размера
![]() называется таблица вида
называется таблица вида
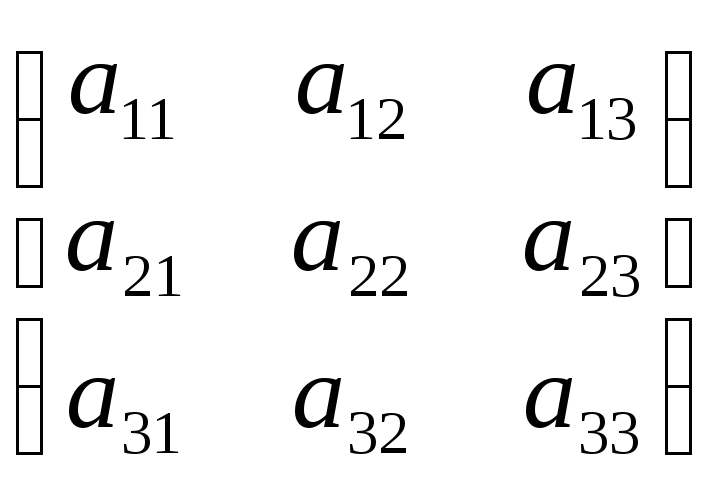 .
.
Определитель этом матрицы есть число, обозначаемое в виде
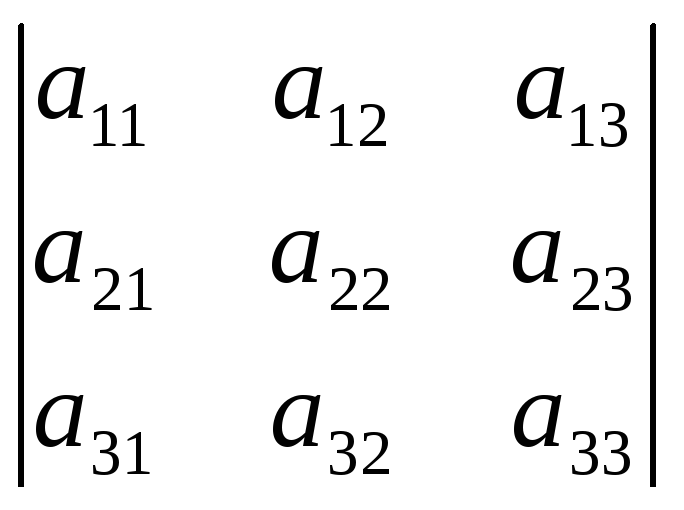 .
.
Этот определитель можно вычислить следующим образом. Выбирается какая-то строка или какой-то столбец. Возьмем, например первую строку. Тогда вычисление определителя проводится по формуле
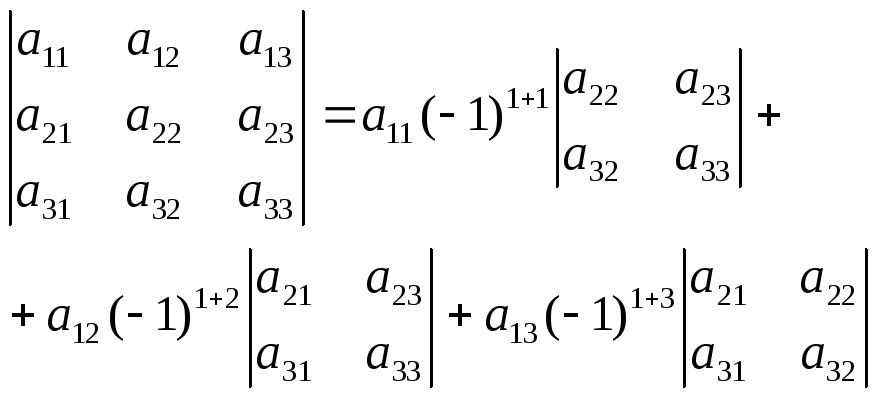
То есть определитель есть сумма трех
слагаемых. Каждое слагаемое образуется
так. Последовательно берутся элементы
выбранной строки или столбца (в данном
случае выбрана первая строка) и умножаются
на
![]() ,
где
,
где![]() - номер строки, в которой находится
данный элемент, а
- номер строки, в которой находится
данный элемент, а![]() - номер столбца, в котором он находится.
Затем полученное число умножается на
определитель размером
- номер столбца, в котором он находится.
Затем полученное число умножается на
определитель размером![]() ,
который получается вычеркиваем строки
и столбца, в которых расположен взятый
элемент. Такой способ вычисления
определителя называется разложением
его по строке или по столбцу.
,
который получается вычеркиваем строки
и столбца, в которых расположен взятый
элемент. Такой способ вычисления
определителя называется разложением
его по строке или по столбцу.
Пример.
Вычислить определитель, разложив его по 2-й строке.
Решение.
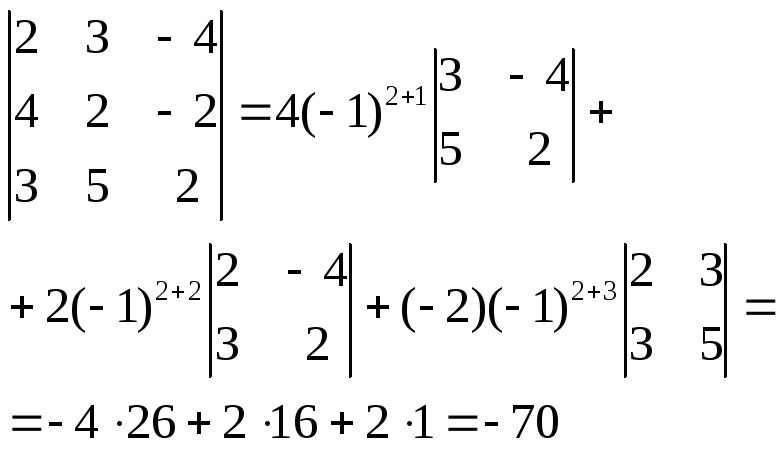
Введем понятие ориентации базиса пространства.
Определение.
Три ненулевых вектора
![]() ,
,![]() и
и![]() называются компланарными, если они,
будучи отложенными от одной точки, лежат
в одной и той же плоскости. Будем говорить,
что имеется упорядоченная тройка
некомпланарных векторов, если все три
вектора ненулевые и не лежат в одной
плоскости (будучи отложенными от общей
точки).
называются компланарными, если они,
будучи отложенными от одной точки, лежат
в одной и той же плоскости. Будем говорить,
что имеется упорядоченная тройка
некомпланарных векторов, если все три
вектора ненулевые и не лежат в одной
плоскости (будучи отложенными от общей
точки).
Заметим, что два вектора всегда лежат в одной плоскости. Третий же вектор может лежать, а может и не лежать в той плоскости, в которой лежат первые два вектора. Плоскость, в которой лежат два вектора, разбивает все пространство на два полупространства.
Определение.
Пусть имеется упорядоченная тройка
некомпланарных векторов
![]() .
Плоскость, в которой расположены векторы
.
Плоскость, в которой расположены векторы![]() и
и![]() ,
делит все пространство на два
полупространства. Тогда третий вектор
,
делит все пространство на два
полупространства. Тогда третий вектор![]() находится в одном из этих полупространств.
Упорядоченная тройка векторов
находится в одном из этих полупространств.
Упорядоченная тройка векторов![]() называется правой при условии, что если
смотреть из полупространства, в котором
расположен вектор
называется правой при условии, что если
смотреть из полупространства, в котором
расположен вектор![]() ,
кратчайший поворот от вектора
,
кратчайший поворот от вектора![]() к вектору
к вектору![]() (то
есть от первого вектора ко второму)
осуществляется против часовой стрелки.
Если же кратчайший поворот от
(то
есть от первого вектора ко второму)
осуществляется против часовой стрелки.
Если же кратчайший поворот от![]() к
к![]() осуществляется
по часовой стрелке, то упорядоченную
тройку векторов
осуществляется
по часовой стрелке, то упорядоченную
тройку векторов![]() называют левой. Все тройки некомпланарных
векторов делятся на правые и левые.
называют левой. Все тройки некомпланарных
векторов делятся на правые и левые.
Рассмотрим тройку базисных векторов
![]() .
В зависимости от взаимной ориентации
векторов эта тройка может быть как
правой, так и левой. В дальнейшем будем
считать, что тройка базисных векторов
.
В зависимости от взаимной ориентации
векторов эта тройка может быть как
правой, так и левой. В дальнейшем будем
считать, что тройка базисных векторов![]() всегда правая. Такой ориентации базисных
векторов соответствует ориентация осей
координат, показанная на Рис. 27.
всегда правая. Такой ориентации базисных
векторов соответствует ориентация осей
координат, показанная на Рис. 27.
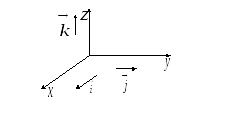
Рис. 27.
В этом случае говорят, что выбрана ориентация базиса в пространстве.
Далее вводится понятие векторного произведения векторов.
Определение.
Пусть даны два ненулевых неколлинеарных
вектора
![]() и
и![]() .
Векторным произведением векторов
.
Векторным произведением векторов![]() и
и![]() называется вектор, обозначаемый
называется вектор, обозначаемый![]() и
удовлетворяющий следующим условиям:
и
удовлетворяющий следующим условиям:
1) Вектор
![]() перпендикулярен одновременно и вектору
перпендикулярен одновременно и вектору![]() и вектору
и вектору![]() ,
а значит перпендикулярен и плоскости,
в которой лежат эти векторы (если их
отложить от общей точки).
,
а значит перпендикулярен и плоскости,
в которой лежат эти векторы (если их
отложить от общей точки).
2)
![]() ,
где
,
где![]() -
угол между векторами
-
угол между векторами![]() и
и![]() .
.
3) Если вектор
![]() отложить от общей точки векторов
отложить от общей точки векторов![]()
![]() (на рисунке 28 это точка
(на рисунке 28 это точка![]() ),
то вектор
),
то вектор![]() направлен
так, что если смотреть из конца вектора
направлен
так, что если смотреть из конца вектора![]() ,
то кратчайший поворот от вектора
,
то кратчайший поворот от вектора![]() к вектору
к вектору![]() (то
есть от первого сомножителя ко второму)
осуществляется против часовой стрелки.
Можно также сказать что векторы
(то
есть от первого сомножителя ко второму)
осуществляется против часовой стрелки.
Можно также сказать что векторы![]() ,
,![]() и
и![]() образуют правую тройку векторов. Таким
образом, вектор
образуют правую тройку векторов. Таким
образом, вектор![]() должен быть направлен так, как показано
на Рис. 28.
должен быть направлен так, как показано
на Рис. 28.
Если хотя бы один из векторов
![]() и
и![]() нулевой
или эти векторы коллинеарны, то по
определению полагается, что
нулевой
или эти векторы коллинеарны, то по
определению полагается, что
![]() .
При этом, формула
.
При этом, формула
![]()
остается справедливой.
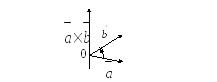
Рис. 28.
Свойства векторного произведения.
1)
![]()
2)
![]()
3) Если
![]() -
число, то
-
число, то
![]()
4) Если тройка базисных векторов
![]() правая, то
правая, то
![]()
![]()
5) Если
![]() ,
,
![]()
и тройка базисных векторов
![]() правая,
то векторное произведение можно вычислить
символически с помощью определителя,
разлагая его по первой строке
правая,
то векторное произведение можно вычислить
символически с помощью определителя,
разлагая его по первой строке
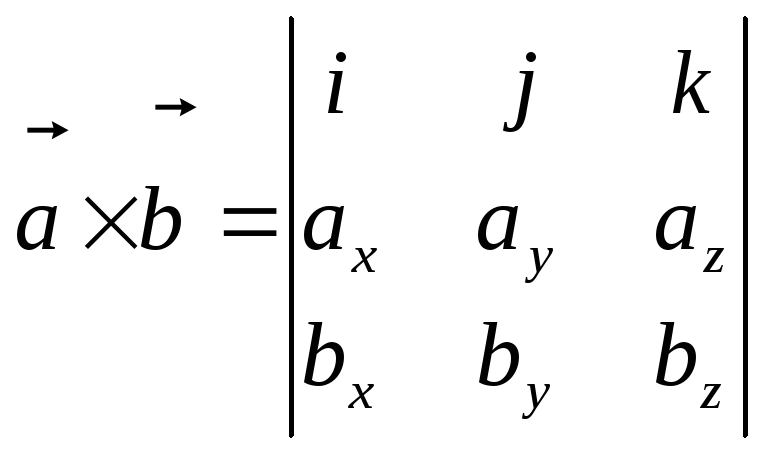 .
.
6) Пусть даны два ненулевых неколлинеарных
вектора![]() и
и![]() .
Отложим их от общей точки и построим
параллелограмм, как это показано на
рисунке 29. Такой параллелограмм называется
.
Отложим их от общей точки и построим
параллелограмм, как это показано на
рисунке 29. Такой параллелограмм называется
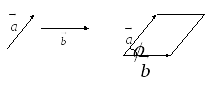
Рис.29.
параллелограммом, построенным на
векторах
![]() и
и![]() .
Тогда площадь
.
Тогда площадь![]() этого параллелограмма
этого параллелограмма![]() равна
равна
![]() ,
,
а площадь
![]() треугольника
треугольника![]() равна
равна
![]()
Свойства 1, 3 и 4 следуют непосредственно и определения векторного произведения. Свойство 5 легко доказать, если справедливо свойство 2. В самом деле, разлагая определитель по 1-й строке, получим
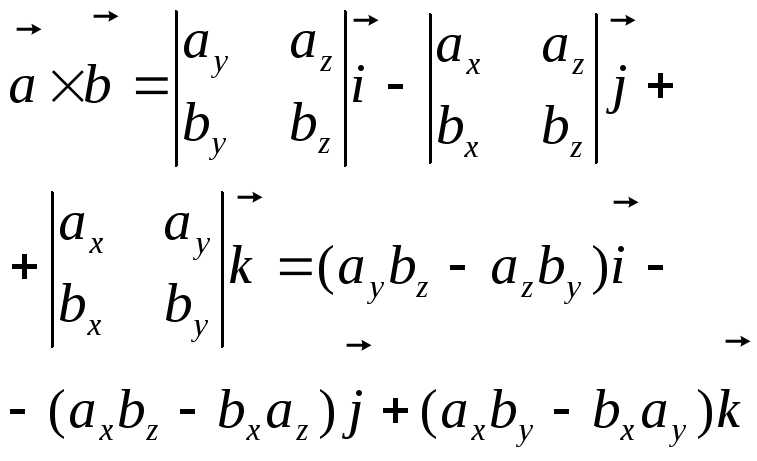
![]() С
другой стороны, если справедливо свойство
2, то с учетом свойств 1, 3 и 4 получаем
С
другой стороны, если справедливо свойство
2, то с учетом свойств 1, 3 и 4 получаем
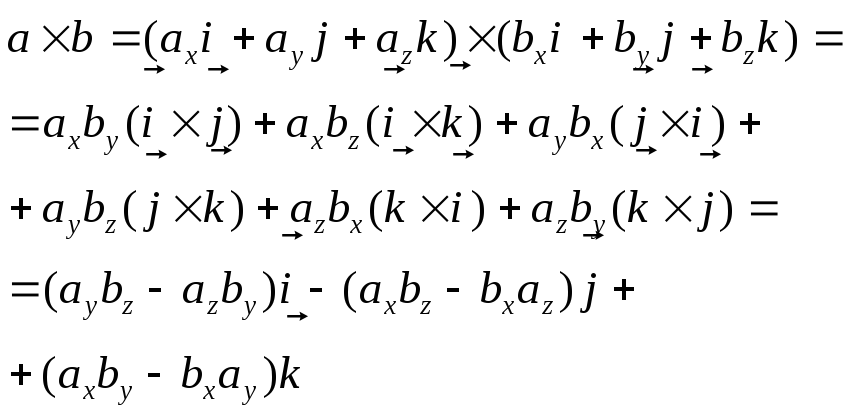
Отсюда следует справедливость свойства 5.
Рассмотрим пример на свойство 5.
Пример.
![]() .
.
Найти
![]() .
.
Решение.
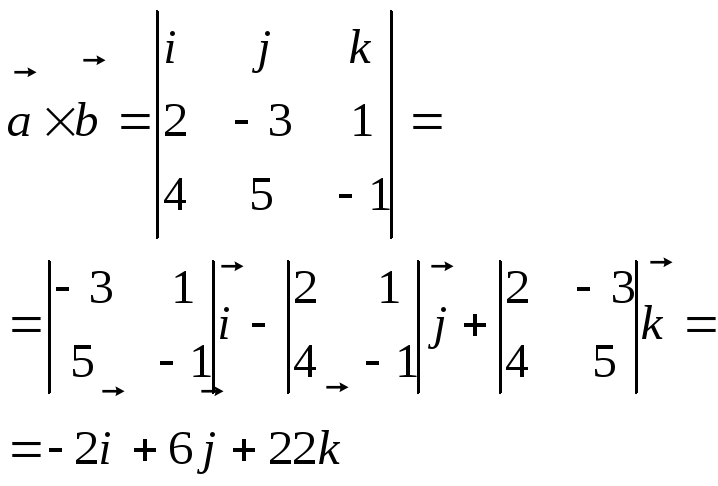
Свойство 2 примем без доказательства.
Обратимся к свойству 6. Из элементарной
геометрии известно, что площадь
параллелограмма
![]() равна
равна
![]() ,
,
где
![]() .
Отсюда
.
Отсюда
![]()
и, следовательно,
![]() .
.
Так как параллелограмм диагональю
![]() разбивается на два равновеликих
треугольника, то
разбивается на два равновеликих
треугольника, то
![]() .
.
Пример.
Найти площадь параллелограмма, построенного на векторах
![]() .
.
Решение.
Найдем
![]() .
.
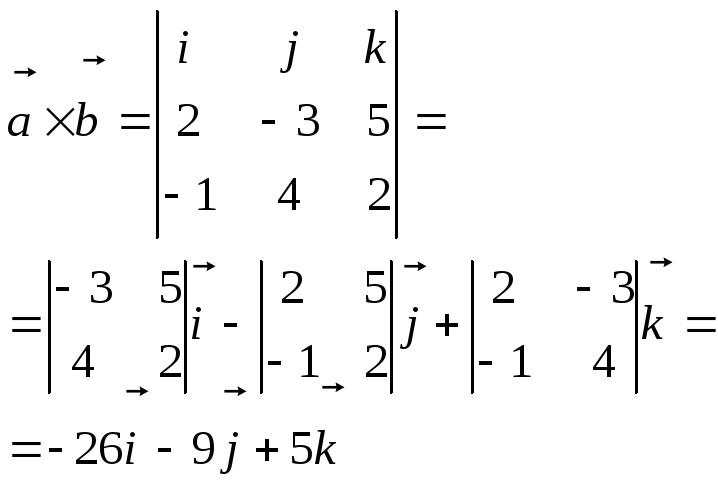
Тогда
![]() .
.
