
- •Глава 1. Векторная алгебра
- •§1. Основные понятия векторной алгебры
- •§2. Проекция вектора на ось.
- •§3. Координаты вектора
- •§4. Скалярное произведение векторов
- •§5. Векторное произведение векторов
- •§5. Смешанное произведение векторов
- •Глава 2. Прямая на плоскости
- •§1. Уравнение прямой на плоскости, проходящей через заданную точку и перпендикулярной заданному вектору
- •§2. Параметрические и канонические уравнения прямой на плоскости
- •§3. Взаимное расположение прямых на плоскости
- •§4. Расстояние от точки до прямой
- •§5. Уравнение прямой с угловым коэффициентом
- •Глава 3. Плоскость в пространстве.
- •§1. Уравнение плоскости в пространстве
- •§ 2. Взаимное расположение плоскостей в пространстве
- •Глава 4. Прямая в пространстве
- •§1. Общие уравнения прямой в пространстве
- •§2. Параметрические и канонические уравнения прямой в пространстве
- •§ 3. Переход от одного вида уравнения прямой к другому виду
- •§4. Взаимное расположение прямых в пространстве. Угол между прямыми.
- •Глава 5. Взаимное расположение прямой и плоскости
§2. Проекция вектора на ось.
Определение.
Будем говорить, что вектор (ненулевой) коллинеарен прямой, если он параллелен прямой или лежит на этой прямой.
Дадим определение оси.
Определение.
Осью называется пара геометрических объектов – прямая и коллинеарный ей вектор. Такой вектор называется направляющим вектором оси или направляющим вектором прямой.

Рис. 11
Направляющий вектор оси обычно располагают на самой прямой. Так как длина направляющего вектора несущественна, то на прямой указывают только конец направляющего вектора в виде стрелки, а начало направляющего вектора не указывает.
Таким образом, на прямой можно выбрать два противоположных направления. Поэтому иногда говорят, что ось – это прямая с выбранным направлением или направленная прямая.
Если направляющий вектор оси
обозначен, например буквой
![]() ,
то саму ось (то есть пару – вектор плюс
прямая) будем обозначать символом «ось
,
то саму ось (то есть пару – вектор плюс
прямая) будем обозначать символом «ось![]() »
(см. Рис. 14)
»
(см. Рис. 14)
Дадим определение орта оси.
Определение.
Если длина направляющего вектора
оси равна единице, то такой направляющий
вектор оси называется ортом оси. Если
ось обозначена как «ось
![]() »,
то орт оси будем обозначать символом
»,
то орт оси будем обозначать символом![]() .
.
Определение.
Пусть вектор
![]() коллинеарен оси (т.е. либо параллелен
оси, либо лежит на ней). Будем говорить,
что вектор
коллинеарен оси (т.е. либо параллелен
оси, либо лежит на ней). Будем говорить,
что вектор![]() сонаправлен с осью, если он сонаправлен
с напраляющим вектором оси и противонаправлен
с осью, если он противонаправлен
направляющему вектору оси.
сонаправлен с осью, если он сонаправлен
с напраляющим вектором оси и противонаправлен
с осью, если он противонаправлен
направляющему вектору оси.
Определим угол между вектором и осью.
Определение.
Пусть даны ось
![]() и вектор
и вектор![]() .
Угол между вектором
.
Угол между вектором![]() и направляющим вектором оси
и направляющим вектором оси![]() называется углом между вектором и осью.
называется углом между вектором и осью.

Рис.12.
Заметим, что вектор
![]() всегда можно отложить от точки, лежащей
на оси. Тогда этот вектор и ось образуют
геометрический угол (Рис. 16). Величина
угла (мера угла) между вектором и осью
может находиться в пределах от 0 до
всегда можно отложить от точки, лежащей
на оси. Тогда этот вектор и ось образуют
геометрический угол (Рис. 16). Величина
угла (мера угла) между вектором и осью
может находиться в пределах от 0 до![]() радиан или от 0одо 180о.
радиан или от 0одо 180о.
Введем важное понятие вектор-проекции вектора на ось.
Определение.
Пусть имеется ось и какая- то точка
![]() .
Если точка не лежит на оси, то проекцией
точки
.
Если точка не лежит на оси, то проекцией
точки![]() на ось называется точка пересечения с
осью перпендикуляра, опущенного из
точки
на ось называется точка пересечения с
осью перпендикуляра, опущенного из
точки![]()
на эту ось. Если точка
![]() лежит
на этой оси, то проекцией точки
лежит
на этой оси, то проекцией точки![]() на
ось называется сама эта точка.
на
ось называется сама эта точка.
Определение.
Пусть даны вектор
![]() и ось
и ось![]() .
.
Обозначим через![]() проекцию
точки
проекцию
точки![]() на
ось
на
ось![]() ,
а через
,
а через![]() проекцию
точки
проекцию
точки![]() на
ось
на
ось![]() .
Вектор
.
Вектор![]() называется
вектор-проекцией вектора
называется
вектор-проекцией вектора![]() на
ось
на
ось![]() (см.
Рис. 17).
(см.
Рис. 17).
Таким образом, вектор
![]() лежит на оси и, следовательно, коллинеарен
оси. Поэтому, если
лежит на оси и, следовательно, коллинеарен
оси. Поэтому, если![]() не
нулевой вектор, то он либо сонаправлен
с осью, либо противонаправлен с ней.
Если вектор
не
нулевой вектор, то он либо сонаправлен
с осью, либо противонаправлен с ней.
Если вектор![]() перпендикулярен
оси, то его вектор-проекция является
нулевым вектором.
перпендикулярен
оси, то его вектор-проекция является
нулевым вектором.
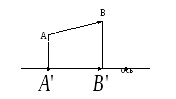
Рис. 13.
Введем важное понятие проекции вектора на ось.
Определение.
Пусть вектор
![]() есть
вектор-проекция вектора
есть
вектор-проекция вектора![]() на
ось
на
ось![]() .
Проекцией вектора
.
Проекцией вектора![]() на ось
на ось![]() называется
число, модуль которого равен длине
вектора
называется
число, модуль которого равен длине
вектора![]() ,
а знак выбирается «+», если вектор
,
а знак выбирается «+», если вектор![]() и ось сонаправлены и выбирается знак
«-», если вектор
и ось сонаправлены и выбирается знак
«-», если вектор![]() и
ось противонаправлены. Проекция вектора
и
ось противонаправлены. Проекция вектора![]() на
ось
на
ось![]() обозначается
символом
обозначается
символом![]() .
Таким образом,
.
Таким образом,![]() ,
если вектор
,
если вектор![]() и ось
и ось![]() сонаправлены и
сонаправлены и![]() ,
если вектор
,
если вектор![]() и
ось
и
ось![]() противонаправлены.
противонаправлены.
Если
![]() ,
то полагаем по определению, что
,
то полагаем по определению, что![]() .
.
Определим также проекцию вектора на вектор.
Определение.
Пусть даны векторы
![]() и
и![]() ,
причем
,
причем![]() ненулевой
вектор. Если через вектор
ненулевой
вектор. Если через вектор![]() провести
прямую, то получим ось с направляющим
вектором
провести
прямую, то получим ось с направляющим
вектором![]() .
Проекция вектора
.
Проекция вектора![]() на эту ось называется проекцией вектора
на эту ось называется проекцией вектора![]() на вектор
на вектор![]() и
обозначается
и
обозначается![]() .
.
Проекцию вектора на ось можно выразить через длину вектора и косинус угла между вектором и осью. Имеет место следующая теорема.
Теорема 8.
Пусть даны вектор
![]() и ось
и ось![]() .
Пусть
.
Пусть![]() - угол между вектором и осью. Тогда
- угол между вектором и осью. Тогда
![]() .
(3)
.
(3)
Доказательство.
Обозначим через
![]() вектор-проекцию вектора
вектор-проекцию вектора![]() на ось. 1)Пусть
на ось. 1)Пусть![]() .
Тогда, как видно из рисунка 14,
вектор-проекция
.
Тогда, как видно из рисунка 14,
вектор-проекция![]() и ось
и ось![]() сонаправлены. Следовательно, как видно
из рисунка,
сонаправлены. Следовательно, как видно
из рисунка,
![]()
![]()

Рис. 14.
2) Пусть
![]() .
В этом случае, как видно из рисунка 15,
.
В этом случае, как видно из рисунка 15,

Рис.15.
вектор-проекция
![]() и ось противонаправлены. Следовательно
и ось противонаправлены. Следовательно![]() .
Но, как видно из рисунка 18,
.
Но, как видно из рисунка 18,
![]() .
.
Здесь учтено, что
![]() .
Тогда
.
Тогда
![]() .
.
3) Если
![]() ,
то
,
то![]() .
Следовательно, и в этом случае верна
формула (3).
.
Следовательно, и в этом случае верна
формула (3).
Рассмотрим теорему, устанавливающую связь вектор-проекции вектора на ось с его проекцией на эту же ось.
Предварительно введем понятие орта вектора.
Определение.
Пусть
![]() ненулевой вектор. Ортом вектора
ненулевой вектор. Ортом вектора![]() будем называть вектор единичной длины,
коллинеарный и сонаправленный с вектором
будем называть вектор единичной длины,
коллинеарный и сонаправленный с вектором![]() .Орт вектора
.Орт вектора![]() будем обозначать как
будем обозначать как![]() .
.
Из самого определения орта вектора
следует, что для любого ненулевого
вектора
![]() имеет место равенство
имеет место равенство
![]()
Имеет место следующая теорема.
Теорема 9.
Вектор-проекция любого вектора на ось равна произведению проекции вектора на эту ось на орт оси, то есть
![]() ,
(4)
,
(4)
Где
![]() -
вектор-проекция вектора
-
вектор-проекция вектора![]() на ось
на ось![]() ,
,![]() -орт оси
-орт оси![]() .
.
Доказательство.
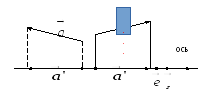
Рис. 16.
Как видно из рисунка 16, если
![]() сонаправлен
с осью
сонаправлен
с осью![]() ,
то из определения проекции и вектор-проекции
вектора на ось следует, что
,
то из определения проекции и вектор-проекции
вектора на ось следует, что
![]() .
.
Здесь учтено, что
![]() .
Если
.
Если![]() противонаправлен
оси
противонаправлен
оси![]() ,
то
,
то
![]()
![]() .
.
В последних равенствах учтено, что
![]() и
и![]() .
.
Рассмотрим связь проекции суммы векторов с проекциями слагаемых.
Теорема 10.
Пусть
![]() .
Тогда для любых
.
Тогда для любых![]() и
и![]()
![]()
Доказательство.
Пусть
![]() .
Вектор
.
Вектор![]() отложим
от точки
отложим
от точки![]() и
обозначим его
и
обозначим его![]() , т.е.
, т.е.![]() .
Проведем через вектор
.
Проведем через вектор![]() прямую. Получим ось, которую обозначим
ось
прямую. Получим ось, которую обозначим
ось![]() .
Пусть
.
Пусть![]() и
и![]() - вектор-проекции векторов
- вектор-проекции векторов![]() и
и![]() на
ось
на
ось![]() .
Тогда
.
Тогда![]() есть вектор-проекция вектора
есть вектор-проекция вектора![]() на
ось
на
ось![]() .
При этом возможны следующие варианты:
.
При этом возможны следующие варианты:
1)
![]() и
и![]() сонаправлены с осью
сонаправлены с осью![]() .
.
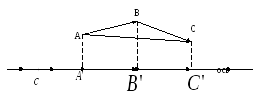
Рис. 17.
2)
![]() сонаправлен, а
сонаправлен, а![]() противонаправлен оси
противонаправлен оси![]() .
.
3)
![]() противонаправлен
, а
противонаправлен
, а![]() сонаправлен
с осью
сонаправлен
с осью![]() .
.
4)
![]() противонаправлен оси
противонаправлен оси![]() и
и![]() противонаправлен оси
противонаправлен оси![]() .
.
Первый из возможных вариантов изображен на рисунке 18. Из рисунка видно, что
![]() .
.
![]()
![]()
![]()
Следовательно
![]() .
.
Оставшиеся варианты рассматриваются аналогично. Рассмотрим, например 2-й вариант. Из рисунка 18 видно, что
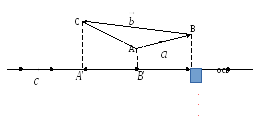
Рис. 18.
![]() .
.
![]() .
.
Следовательно
![]() .
.
Из этого же рисунка видно, что
![]() ,
,
![]() .
.
Отсюда следует, что
![]() .
.
![]()
![]()
