§3. Координаты вектора

До сих пор считалось, что векторы рассматриваются в пространстве. Начиная с этого момента будим считать, что все векторы рассматриваются на плоскости. Будем также полагать, что на плоскости задана Декартова система координат (даже если об этом не говорится), представляющая две взаимно перпендикулярные числовые оси – горизонтальная ось и вертикальная ось. Тогда каждой точкена плоскости ставится в соответствие пара чисел, которые являются ее координатами. Обратно, каждой паре чиселсоответствует точка плоскости такая, что пара чиселявляются ее координатами.

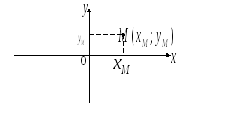
Рис. 19.

Из элементарной геометрии известно, что если на плоскости имеются две точки и, то расстояниемежду этими точками выражается через их координаты по формуле

.

Пусть на плоскости задана Декартова система координат. Орт оси будем обозначать символом, а орт осисимволом. Проекцию произвольноговекторана осьбудем обозначать символом, а проекцию на осьсимволом.

Рис. 20.

Пусть - произвольный вектор на плоскости. Имеет место следующая теорема.

Теорема 22.

Для любого вектора на плоскости существует пара чиселтаких, что справедливо равенство

.

При этом ,.

Доказательство.

Рис. 21.

Пусть дан вектор. Отложим векторот начала координат. Обозначим черезвектор-проекцию векторана ось, а черезвектор-проекцию векторана ось. Тогда, как видно из рисунка 21, имеет место равенство

.

Согласно теореме 9,

,

.

Обозначим ,. Тогда получаем

.

Итак, доказано, что для любого вектора существует пара чиселтаких, что справедливо равенство

,

Причем,

,

.

При другом расположении вектора относительно осей доказательство аналогично.

Определение.

Пара чисел итаких, что, называются координатами вектора. Числоназывается иксовой координатой, а числоигрековой координатой.

Определение.

Пара ортов осей координат называется ортонормированным базисом на плоскости. Представление любого векторав виденазывается разложением векторапо базису.

Непосредственно из определения координат вектора следует, что если координаты векторов равны, то равны и сами векторы. Справедливо также и обратное утверждение.

Теорема.

Равные векторы имеют равные координаты.

Доказательство.

Пусть

,

и . Докажем, что,.

Из равенства векторов следует, что

.

Отсюда

.

Допустим, что , а.

Тогда и значит, что не верно. Аналогично, если, но, то. Отсюда, что не верно. Наконец, если допустить, чтои, то получаем, что

.

Это означает, что векторы иколлинеареы. Но это не верно, так как они перпендикулярны. Следовательно, остается, что,, что и требовалось доказать.

Таким образом, координаты вектора полностью определяют сам вектор. Зная координаты ивектораможно построить сам вектор, построив векторыии сложив их. Поэтому часто сам векторобозначают в виде пары его координат и пишут. Такая запись означает, что.

Непосредственно из определения координат вектора следует следующая теорема.

Теорема.

При сложении векторов их координаты складываются а при умножении вектора на число его координаты умножаются на это число. Записываются эти утверждения в виде

,

.

Доказательство.

,

.

Далее установим как связаны координаты вектора с координатами его концов.

Теорема.

Пусть , причем начало вектора точкаимеет координаты, а конец вектора есть точка. Тогда координаты вектора связаны с координатами его концов следующими соотношениями

,

.

Доказательство.

Пусть и пусть вектор-проекция векторана осьсонаправлен с осью(см. рис. 22). Тогда

,

так как длина отрезка на числовой осиравна координате правого конца минус координата левого конца. Если вектор

Рис. 22.

противонаправлен оси(как на Рис. 23), то

.

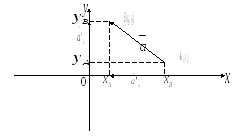Рис. 23.

Если , то в этом случаеи тогда получаем

.

Таким образом, при любом расположении вектора относительно осей координат его координатаравна

.

Аналогично доказывается, что

.

Пример.

Даны координаты концов вектора :. Найти координаты вектора.

Решение.

.

В следующей теореме приводится выражение длины вектора через его координаты.

Теорема 15.

Пусть .Тогда

.

Доказательство.

Пусть и- вектор-проекции векторана осии, соответственно. Тогда, как показано при доказательстве теоремы 9, имеет место равенство

.

При этом, векторы ивзаимно перпендикулярны. При сложении этих векторов по правилу треугольника получаем прямоугольный треугольник (см. Рис. 24).

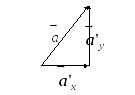
Рис. 24.

По теореме Пифагора имеем

.

Но

,

.

Следовательно

,

.

Отсюда

.

Или

.

Пример.

.Найти.

Решение.

.

Введем понятие направляющих косинусов вектора .

Определение.

Пусть вектор составляет с осьюугол, а с осьюугол(см. Рис. 25).

Рис. 25.

Тогда

,

.

Следовательно,

Так как для любого вектора имеет место равенство

,

Где - орт вектора, то есть вектор единичной длины, сонаправленный с вектором, то

.

Вектор определяет направление вектора. Его координатыиназываются направляющими косинусами вектора. Направляющие косинусы вектора можно выразить через его координаты по формулам

,

.

Имеет место соотношение

.

До настоящего момента в этом параграфе считалось, что все векторы располагаются в одной и той же плоскости. Теперь сделаем обобщение для векторов в пространстве.

Будем считать, что в пространстве задана Декартова система координат с осями ,и.

Орты осей ,ибудем обозначать символами,и, соответственно (Рис. 26).

Можно показать, что все понятия и формулы, которые были получены для векторов на плоскости, обобщаются для

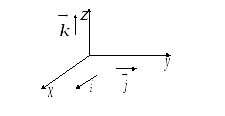Рис. 26.

векторов в пространстве. Тройка векторов называется ортонормированным базисом в пространстве.

Пусть ,и- вектор-проекции векторана оси,и, соответственно. Тогда

.

В свою очередь

,

,

.

Если обозначить

,

,

,

То получаем равенство

.

Коэффициенты перед базисными векторами ,иназываются координатами вектора. Таким образом, для любого векторав пространстве существует тройка чисел,,, называемых координатами векторатаких, что для этого вектора справедливо представление

.

Вектор в этом случае также обозначают в виде. При этом, координаты вектора равны проекциям этого вектора на координатные оси

,

,

,

где - угол между вектороми осью,- угол между вектороми осью,- угол между вектороми осью.

Длина вектора выражается через его координаты по формуле

.

Справедливы утверждения о том, что равные векторы имеют равные координаты, при сложении векторов их координаты складываются, а при умножении вектора на число его координаты умножаются на это число. ,иназываются направляющими косинусами вектора. Они связаны с координатами вектора формулами

,,.

Отсюда следует соотношение

.

Если концы вектора имеют координаты,, то координаты векторасвязаны с координатами концов вектора соотношениями

,

,

.

Пример.

Даны точки и. Найти координаты вектора.

Решение.

.