Глава 1. Векторная алгебра

§1. Основные понятия векторной алгебры

При определении понятий и доказательстве утверждений векторной алгебры мы будем опираться на школьную геометрию (планиметрию и стереометрию).

Определение.

Отрезок называется направленным, если определено (указано) какой конец считается первым, а какой вторым.

Определение.

Вектор – это направленный отрезок. Второй конец вектора будем обозначать стрелкой (см. Рис. 1). Его будем называть концом вектора. Другой конец вектора (где нет стрелки) будем называть началом вектора.

Рис. 1.

Концы вектора будем обозначать большими латинскими буквами, например, начало вектора буквой , а конец буквой. В этом случае сам вектор будем обозначать символом. Кроме того, векторы будем обозначать маленькими латинскими буквами, например.

Определение.

Два вектора называются коллинеарными если они лежат на одной прямой или на параллельных прямых.

Два коллинеарных вектора могут быть направлены в одну и туже сторону или в противоположные стороны. Если коллинеарные векторы направлены в одну и ту же сторону, то будем говорить, что они сонаправлены, если они направлены в противоположные стороны, то будем говорить, что они противонаправлены.

Дадим определение длины вектора.

Определение.

Длиной вектора называется длина соответствующего ему отрезка.

Если вектор обозначен символом , то его длина обозначается символом, если вектор обозначается символом, то его длина обозначается символом. Таким образом,- это геометрический объект (отрезок), в то время какесть число (длина вектора).

Теперь дадим определение равенства двух векторов.

Определение.

Два вектора иназываются равными, если они коллинеарны, сонаправлены и имеют одинаковую длину. В этом случае пишут.

Используя элементарную геометрию, легко доказать следующую теорему.

Теорема 1.

От любой точки пространства можно отложить вектор, равный данному.

Доказательство.

Пусть даны вектор и точка. Если точкаи векторне лежат на одной прямой, то через точку

Рис. 2.

проведем прямую, параллельную вектору. Далее, от точкиотложим отрезок, длина которого равна длине вектора. Стрелку поставим у того конца полученного отрезка, чтобы получившийся вектор был сонаправлен с вектором. Тогда, согласно определению, построенный вектор будет равен вектору. Если точкаи векторлежат на одной прямой, то вектор, равный векторустроим на этой прямой аналогично.

Теперь дадим определение угла между векторами. Пусть векторы иотложены от общей точки. Тогда векторыиобразую геометрический угол. Мера этого угла называется углом между векторамии(см. Рис. 3).

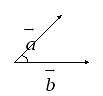
Рис. 3.

Пусть теперь векторы иимеют разные начала.

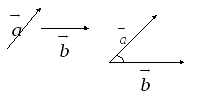
Рис. 4.

Возьмем в пространстве какую-нибудь точку и от этой точки отложим векторыи. Угол между векторамии, отложенными от общей точки и называется углом между векторамии(если их начала не совпадают).

Введем операции сложения и вычитания векторов.

Определение.

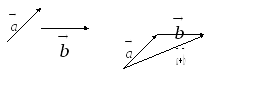Пусть даны два вектораи(Рис. 5).

Рис. 5.

От конца вектора отложим вектор(это можно сделать согласно теореме 1). Затем соединим отрезком начало вектораи конец вектора. У полученного отрезка поставим стрелку у конца вектора. Полученный вектор называется суммой векторовии обозначается.

Такое сложение векторов называется сложением векторов по правилу треугольника.

Введем понятие нулевого вектора.

Определение.

Нулевым вектором называется вектор, у которого начало совпадает с концом, т.е. точка. Нулевой вектор обозначается символом .

Часто используется другой способ сложения векторов – сложение векторов по правилу параллелограмма. Сформулируем это правило в виде теоремы.

Теорема 2.

Пусть даны два вектораи. Выберем в пространстве какую-нибудь точкуи от этой точки отложим векторыи(это можно сделать согласно теореме 1). Затем

Рис.6.

через конец вектора проведем прямую, параллельную вектору, а через конец векторапроведем прямую, параллельную вектору. Получим параллелограмм(см. Рис. 6). Соединим отрезком точкии(диагональ параллелограмма) и поставим стрелку у точки. Тогда векторбудет равен сумме.

Доказательство.

Имеем (согласно свойствам параллелограмма). Но тогда по определению суммы векторов (сложение по правилу треугольника.

Сформулируем свойства операции сложения.

Теорема 3.

Имеют место следующие свойства операции сложения:

1) (коммутативность)

2) (ассоциативность)

3)

Доказательство.

1) Если складывать ипо правилу параллелограмма, то векторыиявляются диагональю одного и того же параллелограмма и поэтому равны.

2) Из Рис. 7 видно, что при сложении векторов ии при сложении векторовиполучается один и тот же вектор.

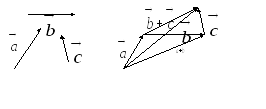
Рис. 7.

3) Если от конца вектора отложить нулевой вектор, то конец нулевого вектора будет совпадать с концом вектора. Поэтому.

Введем понятие вектора, противоположного вектору .

Определение.

Вектором, противоположным вектору называется вектор, коллинеарный вектору, имеющий длину, равную длине вектораи противонаправленный вектору. Вектор, противоположный вектору, будем обозначать символом

.

Имеет место следующее свойство.

Теорема 4.

Для любого вектора справедливо равенство.

Доказательство.

Если от конца вектора отложить вектор, то конец векторасовпадет с началом вектора. Но это и означает, что.

Замечание.

Если вектор обозначается парой букв, например, (первая буквасоответствует началу, вторая буквасоответствует концу), то правило сложения векторов по правилу треугольника можно записать так. В этой записи конец векторасовпадает с началом вектора. В результате получается вектор с началом в точкеи концом в точке.

Если дан вектор , то векторесть вектор, противоположный вектору. В самом деле, вектораиколлинеарны, имеют одинаковую длину, но направлены в противоположные стороны. Итак,.

Определим операцию разности двух векторов.

Определение.

Разностью двух векторов иназывается такой вектор, что справедливо равенство. Разность векторовиобозначается. Таким образом, если, то.

Если даны векторы и, то векторможно построить так. Отложим от одной и той же точки

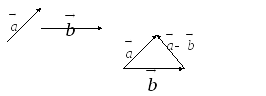
Рис. 8.

векторы и. Соединим отрезком концы этих векторов и у полученного отрезка поставим стрелку у конца вектора. Полученный таким построением вектор и будет вектор. В самом деле, как видно из рисунка.

Вектор можно также построить складывая векторыи, т.е. имеет место следующая теорема.

Теорема 5.

Доказательство.

Пусть даны векторы и. Отложим от общей точки

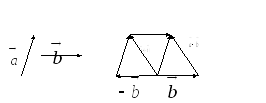
Рис. 9.

векторы,и. Векторыисложим по правилу параллелограмма. Фигураявляется параллелограммом. Поэтому векторыиравны. Отметим, что аналогичное свойство есть у чисел.

Введем еще одну операцию с векторами – умножение вектора на число.

Определение.

Пусть дан вектор и число. Произведение числана векторназывается вектор, обозначаемыйи определяемый следующими условиями (при):

1) вектор коллинеарен вектору

2)

3) вектор сонаправлен с векторомеслиипротивонаправлен вектору, если. Еслиили, то по определению полагают, что. При этом свойство два остается справедливым.

Рассмотрим пример.

Пример.

Дан вектор и число. Построить вектор.

Рис. 10.

Решение.

Возьмем в пространстве произвольную точку и через нее проведем прямую, параллельную вектору. От точкиотложим отрезок, длина которого равна. Стрелку поставим у того конца отрезка, чтобы получившийся вектор был сонаправлен с вектором. Построенный вектор и будет равен вектору. Действительно, он сонаправлен с, а дина его равна числу.

Перечислим свойства операции умножения числа на вектор.

Теорема 6.

Имеют место следующие свойства операции умножения на число:

1)

2)

3)

4)

Эти свойства следуют из определения операций сложения и умножения на число и доказываются с помощью элементарной геометрии.

С помощью операции умножения числа на вектор можно сформулировать необходимое и достаточное условие коллинеарности двух векторов.

Теорема 7.

Пусть даны два ненулевых вектора и. Для того, чтобы они были коллинеарны необходимо и достаточно, чтобы существовало числотакое, что справедливо равенство.

Доказательство.

Если , то согласно определения произведения числа на вектор векторыиколлинеарны.

Обратно. Пусть иколлинеарны и сонаправлены.

Пусть

(1)

Тогда . В самом деле,исонаправлены (т.к.) и имеют одинаковую длину:(по определению умножения вектора на число и т.к.). Длина вектораравна. Это следует из соотношения (1). Еслии противонаправлены, то положим

(2)

Тогда . В самом деле,исонаправлены (т.к., аипротивонаправлены). Длины этих векторов соответственно равны:и. Последнее равенство следует из (2) и из-за того, что(-отрицательное число).