
- •Самарский государственный университет
- •1. Введение в математический анализ
- •1.1. Числовая функция одной переменной.
- •1.2. Числовая функция нескольких переменных.
- •1.3. Числовая последовательность.
- •1.5. Предел числовой последовательности.
- •1.6. Предел числовой функции одной переменной.
- •1.7. Предел числовой функции нескольких переменных.
- •1.8. Бесконечно малые, ограниченные, бесконечно большие и отделимые от нуля величины.
- •1.9. Простейшие свойства бесконечно малых величин.
- •1.10. Простейшие свойства пределов.
- •1.11. Сравнение бесконечно малых величин.
- •1.12. Свойства эквивалентных бмв. Главная часть бмв и ббв.
- •1.13. Предельный переход в неравенстве. Признаки существования предела. Замечательные пределы.
- •1.14. Таблица основных эквивалентных бмв.
- •1.15. Непрерывность функций в точке.
- •1.16. Односторонние пределы и классификация точек разрыва.
- •1.17. Свойства функций непрерывных на отрезке.
- •2. Дифференциальное исчисление
- •2.1. Производная и дифференциал числовой функции одной переменной.
- •2.2. Геометрический смысл производной и дифференциала числовой функции одной переменной.
- •2.3. Сводка правил для вычисления производной.
- •2.4. Частные производные и полный дифференциал числовой функции нескольких переменных.
- •2.5. Геометрический смысл частных производных и полного дифференциала.
- •2.6. Вычисление производных и дифференциалов сложных функций.
- •2.7. Вычисление производных неявных функций.
- •2.8. Производные и дифференциалы высших порядков для числовой функции одной переменной.
- •2.9. Частные производные и полные дифференциалы высших порядков.
- •2.10. Свойства функций, дифференцируемых на интервале.
- •2.11. Раскрытие неопределенностей по правилу Лопиталя
- •2.12. Формула Тейлора.
- •2.13. Представление некоторых функций по формуле Тейлора.
- •2.14. Приложения формулы Тейлора к исследованию функций
- •2.14.1. Главная часть бм
- •2.14.2 Возрастание и убывание функции
- •2.14.3. Экстремумы функции
- •2.14.4. Выпуклость и вогнутость кривой.
- •2.14.5. Точки перегиба кривой.
- •2.15. Формула Тейлора для числовой функции нескольких переменных.
- •2.16. Локальные экстремумы функции нескольких переменных.
- •2.17. Аппроксимация опытных данных по методу наименьших квадратов.
- •2.18. Производная скалярного поля по направлению. Градиент.
- •2.19. Условные экстремумы числовой функции нескольких переменных.
- •2.20. Формулировка задачи линейного программирования
1.6. Предел числовой функции одной переменной.
Очевидно, что в
отличие от последовательности, у которой
может быть только один предел при
![]() ,
у функции одной переменной
,
у функции одной переменной![]() может быть бесчисленное множество
пределов. Это могут быть пределы в любой
конечной точке –
может быть бесчисленное множество
пределов. Это могут быть пределы в любой
конечной точке –![]() и в бесконечно удаленных точках –
и в бесконечно удаленных точках –![]() .
.
Сформулируем сначала определение предела функции в бесконечности, поскольку оно по структуре очень похоже на определение предела последовательности.
Число
![]() называется пределом функции
называется пределом функции
![]() в бесконечно удаленной точке
в бесконечно удаленной точке![]() ,
если для любого сколь угодно малого
положительного числа
,
если для любого сколь угодно малого
положительного числа![]() можно указать такое положительное число
можно указать такое положительное число![]() ,
зависящее от
,
зависящее от![]() ,
что при всех
,
что при всех
![]() ,
удовлетворяющих условию
,
удовлетворяющих условию
![]() ,
будет выполняться неравенство
,
будет выполняться неравенство![]() .
.
Математическая символика этого определения такова:
![]() . (1.6.1)
. (1.6.1)
Отметим, что
определение охватывает сразу оба
возможных варианта –
![]() .
.
Суть этого
определения заключается в том, что,
начиная с некоторого числа
![]() ,все
значения функции без исключения окажутся
внутри сколь угодно малой окрестности
,все
значения функции без исключения окажутся
внутри сколь угодно малой окрестности
![]() .
Неравенство
.
Неравенство![]() называется окрестностью бесконечно
удаленной точки
называется окрестностью бесконечно
удаленной точки
![]() . (1.6.2)
. (1.6.2)

Определение предела в конечной точке звучит следующим образом.
Число
![]() называется пределом функции
называется пределом функции
![]() в точке
в точке
![]()
![]() ,
если для любого сколь угодно малого
положительного числа
,
если для любого сколь угодно малого
положительного числа![]() можно указать такое положительное число
можно указать такое положительное число![]() ,
зависящее от
,
зависящее от![]() ,
что при всех
,
что при всех
![]() ,
удовлетворяющих условию
,
удовлетворяющих условию
![]() ,
выполняется неравенство
,
выполняется неравенство![]() .
.
Математическая символика этого определения такова:
![]() .
(1.6.3)
.
(1.6.3)
1.7. Предел числовой функции нескольких переменных.
Сформулируем здесь определения предела для функции нескольких переменных в точке и в бесконечности.
Число
![]() называется пределом функции двух
переменных
называется пределом функции двух
переменных![]() в точке
в точке![]() –
– ,
если для любого сколь угодно малого
положительного числа
,
если для любого сколь угодно малого
положительного числа![]() можно указать такое положительное число
можно указать такое положительное число![]() ,
зависящее от
,
зависящее от![]() ,
что при всех
,
что при всех![]() удовлетворяющих условию
удовлетворяющих условию![]() будет выполняться неравенство
будет выполняться неравенство![]() .
.
Математическая символика этого определения такова:
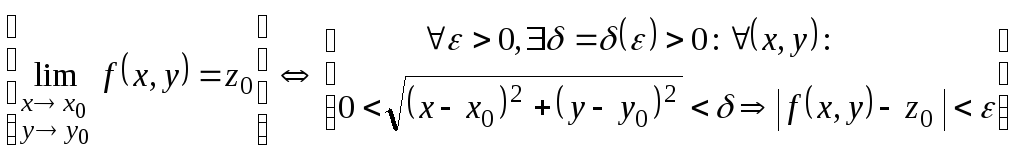 . (1.7.1)
. (1.7.1)
Отметим, что
неравенство
![]() геометрически означает внутренность
круга радиуса
геометрически означает внутренность
круга радиуса![]() с центром в точке
с центром в точке![]() .
Такое множество тоже является окрестностью
радиуса
.
Такое множество тоже является окрестностью
радиуса![]() с центром в точке
с центром в точке![]()
![]() . (1.7.2)
. (1.7.2)
Число
![]() называется пределом функции двух
переменных
называется пределом функции двух
переменных![]() в бесконечно удаленной точке –
в бесконечно удаленной точке – ,
если для любого сколь угодно малого
положительного числа
,
если для любого сколь угодно малого
положительного числа![]() можно указать такое положительное число
можно указать такое положительное число![]() ,
зависящее от
,
зависящее от![]() ,
что при всех
,
что при всех![]() удовлетворяющих условию
удовлетворяющих условию![]() будет выполняться неравенство
будет выполняться неравенство![]() .
.
Математическая символика этого определения такова:
 .(1.7.3)
.(1.7.3)
Неравенство
![]() называется окрестностью бесконечно
удаленной точки радиуса
называется окрестностью бесконечно
удаленной точки радиуса![]()
![]() . (1.7.4)
. (1.7.4)
1.8. Бесконечно малые, ограниченные, бесконечно большие и отделимые от нуля величины.
Мы рассмотрели понятие предела пяти математических объектов:
1. Числовой
последовательности при
![]() .
.
2. Числовой функции
одной переменной при
![]() .
.
3. Числовой функции
одной переменной при
![]() .
.
4. Числовой функции
двух переменных
в точке
![]() .
.
5. Числовой функции
двух переменных
в бесконечности![]() .
.
Структура всех определений предела одинакова и различается только областью изменения аргумента.
Поэтому целесообразно обобщить эти пять объектов в одно новое понятие и назвать величиной любой из следующих объектов:
1. Числовую
последовательность при
![]() .
.
2. Числовую функцию
одной переменной при
![]() .
.
3. Числовую функцию
одной переменной при
![]() .
.
4. Числовую функцию
двух переменных при
![]() .
.
5. Числовую функцию
двух переменных при
![]() .
.
Обозначают величины
как обычные функции –
![]() .
Аргументx
расшифровывается по смыслу текущей
задачи. Определение предела величины
формулируется следующим образом.
.
Аргументx
расшифровывается по смыслу текущей
задачи. Определение предела величины
формулируется следующим образом.
Число
![]() называется пределом величины
называется пределом величины![]() –
–![]() ,
если для любого сколь угодно малого
положительного числа
,
если для любого сколь угодно малого
положительного числа![]() в соответствующей области будет
выполняться неравенство
в соответствующей области будет
выполняться неравенство![]() .
.
Математическая символика этого определения такова:
![]() . (1.8.1)
. (1.8.1)
Величина называется бесконечно малой (БМВ), если её предел равен нулю
![]() , (1.8.2)
, (1.8.2)
или
![]() в соответствующей области
выполняется
неравенство
в соответствующей области
выполняется
неравенство
![]() .
.
Обычно БМВ обозначают начальными буквами греческого алфавита.
Теорема 1 (о связи БМВ с величиной, имеющей конечный предел).
Всякая величина, имеющая конечный предел, отличается от него на БМВ.
Доказательство:
Пусть
![]() .
.
По определению
![]() в соответствующей области
выполняется
в соответствующей области
выполняется
![]() .
Обозначим
.
Обозначим![]() .
Тогда
.
Тогда![]() и
и![]() ,
следовательно
,
следовательно![]() – БМВ, что и требовалось доказать.
– БМВ, что и требовалось доказать.
Величина
![]() называетсяограниченной
на множестве А,
если
называетсяограниченной
на множестве А,
если
![]() . (1.8.3)
. (1.8.3)
Теорема 2 (о связи ограниченной величины и величины, имеющей конечный предел).
Всякая величина, имеющая конечный предел, является ограниченной в соответствующей области.
Доказательство:
![]() .
.
Обратная теорема
не имеет места:
![]() ,
но
,
но![]() не существует.
не существует.
Величина обратная к БМВ называется бесконечно большой величиной(ББВ).
Если
![]() – БМВ, то
– БМВ, то![]() – ББВ и наоборот. Поэтому часто пишут
символические равенства
– ББВ и наоборот. Поэтому часто пишут
символические равенства![]() .
.
Всякая ББВ является неограниченной величиной. Обратное утверждение неверно.
Например,
![]() при
при![]() является неограниченной величиной, но
не ББВ.
является неограниченной величиной, но
не ББВ.
Величина
![]() называетсяотделимой
от нуля
на множестве А,
если
называетсяотделимой
от нуля
на множестве А,
если
![]() . (1.8.4)
. (1.8.4)
Теорема 3 (о связи отделимой от нуля и ограниченной величин).
Величина, обратная отделимой от нуля, является ограниченной.
Доказательство:
![]() .
.
Теорема 4 (об устойчивости знака величины, имеющей ненулевой предел).
Всякая величина, имеющая конечный ненулевой предел, отделима от нуля и принимает на соответствующем множестве значения только того знака, что и знак предела.
Доказательство:
1. Пусть
![]() .
Выберем
.
Выберем![]() ,
тогда будем иметь
,
тогда будем иметь
![]() .
.
Что и требовалось доказать.
2. Случай, когда
![]() доказать самостоятельно.
доказать самостоятельно.
