
- •Самарский государственный университет
- •1. Введение в математический анализ
- •1.1. Числовая функция одной переменной.
- •1.2. Числовая функция нескольких переменных.
- •1.3. Числовая последовательность.
- •1.5. Предел числовой последовательности.
- •1.6. Предел числовой функции одной переменной.
- •1.7. Предел числовой функции нескольких переменных.
- •1.8. Бесконечно малые, ограниченные, бесконечно большие и отделимые от нуля величины.
- •1.9. Простейшие свойства бесконечно малых величин.
- •1.10. Простейшие свойства пределов.
- •1.11. Сравнение бесконечно малых величин.
- •1.12. Свойства эквивалентных бмв. Главная часть бмв и ббв.
- •1.13. Предельный переход в неравенстве. Признаки существования предела. Замечательные пределы.
- •1.14. Таблица основных эквивалентных бмв.
- •1.15. Непрерывность функций в точке.
- •1.16. Односторонние пределы и классификация точек разрыва.
- •1.17. Свойства функций непрерывных на отрезке.
- •2. Дифференциальное исчисление
- •2.1. Производная и дифференциал числовой функции одной переменной.
- •2.2. Геометрический смысл производной и дифференциала числовой функции одной переменной.
- •2.3. Сводка правил для вычисления производной.
- •2.4. Частные производные и полный дифференциал числовой функции нескольких переменных.
- •2.5. Геометрический смысл частных производных и полного дифференциала.
- •2.6. Вычисление производных и дифференциалов сложных функций.
- •2.7. Вычисление производных неявных функций.
- •2.8. Производные и дифференциалы высших порядков для числовой функции одной переменной.
- •2.9. Частные производные и полные дифференциалы высших порядков.
- •2.10. Свойства функций, дифференцируемых на интервале.
- •2.11. Раскрытие неопределенностей по правилу Лопиталя
- •2.12. Формула Тейлора.
- •2.13. Представление некоторых функций по формуле Тейлора.
- •2.14. Приложения формулы Тейлора к исследованию функций
- •2.14.1. Главная часть бм
- •2.14.2 Возрастание и убывание функции
- •2.14.3. Экстремумы функции
- •2.14.4. Выпуклость и вогнутость кривой.
- •2.14.5. Точки перегиба кривой.
- •2.15. Формула Тейлора для числовой функции нескольких переменных.
- •2.16. Локальные экстремумы функции нескольких переменных.
- •2.17. Аппроксимация опытных данных по методу наименьших квадратов.
- •2.18. Производная скалярного поля по направлению. Градиент.
- •2.19. Условные экстремумы числовой функции нескольких переменных.
- •2.20. Формулировка задачи линейного программирования
1.2. Числовая функция нескольких переменных.
Отображение
![]() называетсячисловой
функцией нескольких переменных,
если
называетсячисловой
функцией нескольких переменных,
если
![]() и
и
![]() .
Обозначается функция нескольких
переменных –
.
Обозначается функция нескольких
переменных –![]() ,
множествоX
называется областью определения функции,
множество Y
– множеством значений функции. При
,
множествоX
называется областью определения функции,
множество Y
– множеством значений функции. При
![]() получаем функцию двух переменных –
получаем функцию двух переменных –![]() или
или![]() .
.
На практике функции нескольких переменных часто называют скалярными полями (поле электростатического потенциала, нестационарное температурное поле в неравномерно нагретом теле и т.д.).
Функция двух
переменных
![]() в пространстве
в пространстве![]() имеет график. Этим графиком является
множество точек
имеет график. Этим графиком является
множество точек
![]() , (1.2.1)
, (1.2.1)
определяющее некоторую поверхность в пространстве.
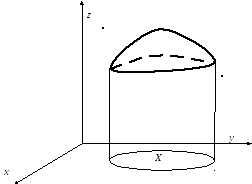
Иногда уравнение поверхности удобно представлять в неявном виде
![]() .
.
Если его можно разрешить относительно переменной z, то получится функция двух переменных
![]() .
.
Например, уравнение сферы радиуса r с центром в начале координат имеет вид
![]() .
.
Если его разрешить относительно z, то получим две функции
![]() .
.
Первая функция определяет верхнюю полусферу, вторая – нижнюю.
1.3. Числовая последовательность.
Отображение
![]() ,
гдеN
– множество
натуральных чисел,
а
,
гдеN
– множество
натуральных чисел,
а
![]() ,
называетсячисловой
последовательностью.
Таким образом, числовая последовательность
это функция натурального аргумента и
обозначают ее с помощью индексов –
,
называетсячисловой
последовательностью.
Таким образом, числовая последовательность
это функция натурального аргумента и
обозначают ее с помощью индексов –
![]() .
.
Например,
![]()
Выражение
![]() называется общим
членом
последовательности.
называется общим
членом
последовательности.
Дадим несколько определений.
1. Последовательность
![]() называетсяограниченной
сверху,
если
называетсяограниченной
сверху,
если
![]()
2. Последовательность
![]() называетсяограниченной
снизу,
если
называетсяограниченной
снизу,
если
![]()
3. Последовательность
![]() называетсяограниченной,
если все её члены лежат в некотором
конечном интервале.
называетсяограниченной,
если все её члены лежат в некотором
конечном интервале.
4. Последовательность
называется монотонно
возрастающей (неубывающей),
если
![]() .
.
5. Последовательность
называется строго
возрастающей,
если
![]() .
.
6. Последовательность
называется монотонно
убывающей (невозрастающей),
если
![]() .
.
7. Последовательность
называется строго
убывающей,
если
![]() .
.
Замечание.
В этих определениях
числа М и
m
называются
соответственно верхней
и нижней границами последовательности
![]() .
Таких границ можно указать сколько
угодно много. Наименьшее из всех значенийМ
называется точной
верхней границей,
а наибольшее
из всех значений m
– точной
нижней границей .
.
Таких границ можно указать сколько
угодно много. Наименьшее из всех значенийМ
называется точной
верхней границей,
а наибольшее
из всех значений m
– точной
нижней границей .
1.5. Предел числовой последовательности.
Рассмотрим числовую
последовательность
![]() .
Фактически с ней можно выполнять две
операции:
.
Фактически с ней можно выполнять две
операции:
1. Вычислять члены последовательности при различных n.
2. Выяснять поведение последовательности при неограниченном увеличении n.
В последнем случае возможны три варианта:
1. Члены последовательности будут стремиться к бесконечности.
![]()
2. Члены последовательности будут совершать бесконечные колебания.
![]()
3. Члены последовательности будут стремиться к конечному числу.
![]()
В последнем случае говорят о существовании предела последовательности.
Определение предела последовательности формулируется следующим образом.
Число
![]() называетсяпределом
последовательности
называетсяпределом
последовательности
![]()
![]() если для любого сколь угодно малого
положительного числа
если для любого сколь угодно малого
положительного числа![]() можно указать такое натуральное число
можно указать такое натуральное число![]() ,
зависящее от этого
,
зависящее от этого![]() ,
что при всех
,
что при всех![]() выполняется условие
выполняется условие![]() .
.
Математическая символика этого определения такова:
![]() . (1.5.1)
. (1.5.1)
Суть этого
определения заключается в том, что,
начиная с некоторого номера
![]() ,все
члены последовательности без исключения
окажутся внутри сколь угодно малого
симметричного интервала
,все
члены последовательности без исключения
окажутся внутри сколь угодно малого
симметричного интервала
![]() .
Такой интервал называется окрестностью
точки
.
Такой интервал называется окрестностью
точки![]() ,
радиуса –
,
радиуса –![]() .
Обозначается это так
.
Обозначается это так
![]() . (1.5.2)
. (1.5.2)
Теорема (о единственности предела). Всякая числовая последовательность может иметь не более одного предела.
Доказательство:
Для доказательства предположим, что последовательность имеет более одного предела
![]() .
.
Воспользуемся определением для первого предела
![]() .
.
Воспользуемся определением для второго предела
![]() .
.
Обозначим
![]() .
Тогда при
.
Тогда при![]() оба неравенства будут выполняться
одновременно и их можно сложить
оба неравенства будут выполняться
одновременно и их можно сложить
![]()
Пользуясь известным
числовым неравенством
![]() ,
получим
,
получим
![]() .
.
Таким свойством
(быть меньше любого заранее заданного
положительного числа) обладает только
нуль. Следовательно
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Пример.
Доказать, что
![]() .
.
