
- •Самарский государственный университет
- •1. Введение в математический анализ
- •1.1. Числовая функция одной переменной.
- •1.2. Числовая функция нескольких переменных.
- •1.3. Числовая последовательность.
- •1.5. Предел числовой последовательности.
- •1.6. Предел числовой функции одной переменной.
- •1.7. Предел числовой функции нескольких переменных.
- •1.8. Бесконечно малые, ограниченные, бесконечно большие и отделимые от нуля величины.
- •1.9. Простейшие свойства бесконечно малых величин.
- •1.10. Простейшие свойства пределов.
- •1.11. Сравнение бесконечно малых величин.
- •1.12. Свойства эквивалентных бмв. Главная часть бмв и ббв.
- •1.13. Предельный переход в неравенстве. Признаки существования предела. Замечательные пределы.
- •1.14. Таблица основных эквивалентных бмв.
- •1.15. Непрерывность функций в точке.
- •1.16. Односторонние пределы и классификация точек разрыва.
- •1.17. Свойства функций непрерывных на отрезке.
- •2. Дифференциальное исчисление
- •2.1. Производная и дифференциал числовой функции одной переменной.
- •2.2. Геометрический смысл производной и дифференциала числовой функции одной переменной.
- •2.3. Сводка правил для вычисления производной.
- •2.4. Частные производные и полный дифференциал числовой функции нескольких переменных.
- •2.5. Геометрический смысл частных производных и полного дифференциала.
- •2.6. Вычисление производных и дифференциалов сложных функций.
- •2.7. Вычисление производных неявных функций.
- •2.8. Производные и дифференциалы высших порядков для числовой функции одной переменной.
- •2.9. Частные производные и полные дифференциалы высших порядков.
- •2.10. Свойства функций, дифференцируемых на интервале.
- •2.11. Раскрытие неопределенностей по правилу Лопиталя
- •2.12. Формула Тейлора.
- •2.13. Представление некоторых функций по формуле Тейлора.
- •2.14. Приложения формулы Тейлора к исследованию функций
- •2.14.1. Главная часть бм
- •2.14.2 Возрастание и убывание функции
- •2.14.3. Экстремумы функции
- •2.14.4. Выпуклость и вогнутость кривой.
- •2.14.5. Точки перегиба кривой.
- •2.15. Формула Тейлора для числовой функции нескольких переменных.
- •2.16. Локальные экстремумы функции нескольких переменных.
- •2.17. Аппроксимация опытных данных по методу наименьших квадратов.
- •2.18. Производная скалярного поля по направлению. Градиент.
- •2.19. Условные экстремумы числовой функции нескольких переменных.
- •2.20. Формулировка задачи линейного программирования
2.18. Производная скалярного поля по направлению. Градиент.
Рассмотрим
дифференцируемую функцию трех переменных
(скалярное поле)
![]() .
Каждая из ее трех частных производных
.
Каждая из ее трех частных производных
![]()
характеризует скорость роста функции в направлении координатных осей.
Выясним, какая величина характеризует скорость роста этого скалярного поля в направлении произвольной прямой.

Рассмотрим
произвольную прямую в пространстве,
направление которой задается единичным
вектором
![]() .
.
Возьмем на прямой
точку
![]() и точку
и точку
![]() .
Эти точки образуют вектор
.
Эти точки образуют вектор
![]() ,
коллинеарный вектору
,
коллинеарный вектору![]() .
.
Полное приращение функции
![]()
выражается через частные производные формулой (2.4.13)
![]() ,
,
или
![]() . (2.18.1)
. (2.18.1)
Разделим обе части
равенства (2.18.1) на
![]()
![]() .
.
Учитывая, что
![]() ,
,
находим
![]() . (2.18.2)
. (2.18.2)
Если существует предел
![]() , (2.18.3)
, (2.18.3)
то
этот предел называется производной
скалярного поля по направлению
вектора
![]() .
.
Переходя в равенстве
(2.18.2) к пределу при
![]() ,
получаем формулу для вычисления
производной по направлению
,
получаем формулу для вычисления
производной по направлению
![]() . (2.18.4)
. (2.18.4)
Три частных
производных
![]() в качестве координат образуют вектор
в качестве координат образуют вектор
![]() , (2.18.5)
, (2.18.5)
который
называется градиентом
скалярного
поля в рассматриваемой точке
![]() .
.
Очевидно, что вектор – градиент и производная по направлению связаны соотношением
![]() . (2.18.6)
. (2.18.6)
Обозначим угол
между векторами
![]() и
и
![]() –
–
![]() .
Тогда
.
Тогда
![]() . (2.18.7)
. (2.18.7)
Формула (2.18.7)
показывает, что максимальное значение
производной по направлению соответствует
углу
![]() .
Таким образом, вектор градиента указывает
в пространстве направление максимального
возрастания скалярного поля. Угол
.
Таким образом, вектор градиента указывает
в пространстве направление максимального
возрастания скалярного поля. Угол![]() соответствует направлению максимального
убывания скалярного поля. Угол
соответствует направлению максимального
убывания скалярного поля. Угол![]() соответствует направлению, в котором
скалярное поле не изменяется.
соответствует направлению, в котором
скалярное поле не изменяется.
Если рассмотреть
поверхности уровня
![]() ,
на которых скалярное поле постоянно,
то уравнение касательной плоскости к
такой поверхности в точке
,
на которых скалярное поле постоянно,
то уравнение касательной плоскости к
такой поверхности в точке![]() имеет вид
имеет вид
![]() .
.
Частные производные
![]() выражаются через частные производные
выражаются через частные производные![]() по формула производных неявных функций
по формула производных неявных функций
 ,
,
 .
.
Тогда уравнение касательной плоскости принимает вид
![]() .
.
Главным вектором этой касательной плоскости является вектор градиента, следовательно, градиент направлен по нормали к поверхности уровня.
2.19. Условные экстремумы числовой функции нескольких переменных.
Пусть функция двух
переменных
![]() выражает в количественном отношении
некоторую цель (прибыль фирмы, транспортные
расходы, производственные издержки и
т.д.). Эта функция так и называется –целевая
функция.
Обычных локальных экстремумов эта
функция может не иметь. На ее аргументы
(обычно в их роли выступают некоторые
ресурсы – закупаемое сырье, стоимость
перевозок, зарплата работникам,
электроэнергия, износ оборудования и
т.д.) накладываются некоторые ограничения,
которые связывают их функциональной
зависимостью
выражает в количественном отношении
некоторую цель (прибыль фирмы, транспортные
расходы, производственные издержки и
т.д.). Эта функция так и называется –целевая
функция.
Обычных локальных экстремумов эта
функция может не иметь. На ее аргументы
(обычно в их роли выступают некоторые
ресурсы – закупаемое сырье, стоимость
перевозок, зарплата работникам,
электроэнергия, износ оборудования и
т.д.) накладываются некоторые ограничения,
которые связывают их функциональной
зависимостью
![]() .
Таким образом, формулируется задача
отыскания экстремумов целевой функции
при наложенных на аргументы ограничениях.
.
Таким образом, формулируется задача
отыскания экстремумов целевой функции
при наложенных на аргументы ограничениях.
 . (2.19.1)
. (2.19.1)
Т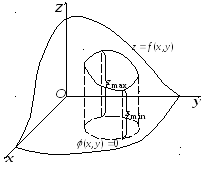 акие
экстремумы называютсяусловными
экстремумами.
акие
экстремумы называютсяусловными
экстремумами.
Если уравнение
![]() можно разрешить относительно переменнойy,
то поиск условного экстремума сведется
к поиску обычного экстремума для функции
одной переменной
можно разрешить относительно переменнойy,
то поиск условного экстремума сведется
к поиску обычного экстремума для функции
одной переменной
![]() .
Однако, как правило, решить нелинейное
уравнение аналитически невозможно,
поэтому для поиска условных экстремумов
разработан специальный алгоритм –метод
множителей Лагранжа.
.
Однако, как правило, решить нелинейное
уравнение аналитически невозможно,
поэтому для поиска условных экстремумов
разработан специальный алгоритм –метод
множителей Лагранжа.
Продифференцируем
![]() как сложную функцию, учитывая, что
как сложную функцию, учитывая, что![]()
![]() .
.
Необходимое условие
экстремума
![]() ,
дает
,
дает
![]() . (219.2)
. (219.2)
Выражая из уравнения
(2.19.2) производную
![]()
![]() ,
находим
,
находим
 . (2.19.3)
. (2.19.3)
Вычислим теперь
эту же производную как производную
функции заданную неявно уравнением
![]()
 . (2.19.4)
. (2.19.4)
Сравнивая производные (2.19.3) и (2.19.4), получаем равенство
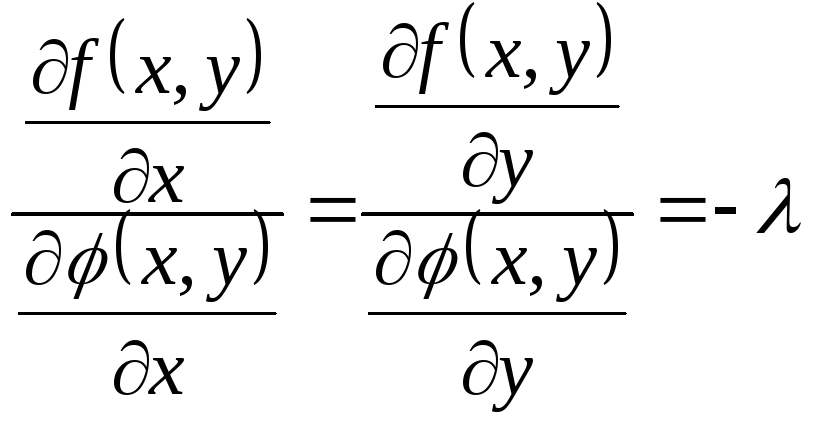 ,
,
равносильное системе двух уравнений
 .
.
Присоединяя к этой
системе ограничение
![]() ,
получаем замкнутую систему уравнений
,
получаем замкнутую систему уравнений
 , (2.19.5)
, (2.19.5)
относительно
неизвестных
![]() .
Решением системы (2.19.5) и будут условные
экстремумы поставленной задачи.
.
Решением системы (2.19.5) и будут условные
экстремумы поставленной задачи.
Систему (2.19.5) легко получить с помощью вспомогательной функции Лагранжа
![]() . (2.19.6)
. (2.19.6)
Очевидно, что необходимые условия для обычных локальных экстремумов для функции Лагранжа (2.19.6) приводят нас снова к системе (2.19.5)
 . (2.19.7)
. (2.19.7)
Совершенно аналогично решается задача нахождения условных экстремумов в общем случае, когда целевая функция является функцией нескольких переменных, а на аргументы накладывается несколько условий. Задача отыскания условных экстремумов формулируется следующим образом
 . (2.19.8)
. (2.19.8)
Функция Лагранжа для такой задачи имеет вид
![]() . (2.19.9)
. (2.19.9)
Параметры
![]() называютсямножителями
Лагранжа.
называютсямножителями
Лагранжа.
Пример. Найти кратчайшее расстояние от начала координат до кривой
![]() .
.
Решение:
Целевая функция здесь имеет вид
![]() .
.
Составляем функцию Лагранжа
![]() .
.
Записываем необходимые условия локальных экстремумов
 .
.
Из двух первых уравнений системы, находим
![]() .
.
Исключаем из
системы переменную
![]() .
.
![]()
Окончательно находим
 .
.

Из рисунка видно, что в первой точке целевая функция достигает максимума, а во второй – минимума, причем
![]() ,
,
![]() .
.
