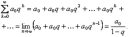МатематикаШпоры
.docx|
1)Обозначим через D некоторое множество точек в п-мерном пространстве.Если задан закон f , в силу которого каждой точке М(х;...;х) D ставится в соответствие число и, то говорят, что на множестве D определена функция и= f(х;...;х).Множество точек М(х;...;х), для которых функция и= f(х;...;х) определена, называют областью определения этой функции и обозначают D(f).Функции многих переменных можно обозначать одним символом и=f(М), указывая размерность пространства, которому принадлежит точка М.Функции двух переменных можно изобразить графически в виде некоторой поверхности.Графиком функции двух переменных z=f(х;у) в прямоугольной системе координат Оху называется геометрическое место точек в трехмерном пространстве, координаты которых (х;у;z) удовлетворяют уравнению z=f(х;у). Необходимые условия дифференцируемости функции.необходимое условиеТеорема. Если функция z=f(x, y) дифференцируема в некоторой точке, то она в этой точкенепрерывна. Если в точке (x, y) функция z=f(x, y) дифференцируема, то полное приращение функции zв этой точке, отвечающее приращениям ∆x и ∆y аргументов, можно представить в виде ∆z=A∆x+B∆y+α(∆x, ∆y)∆x+β(∆x, ∆y)∆yДостаточное условиеТеорема. Если функция z=f(x, y) имеет частные производные fx/и fy/в некоторойокрестности точки (x0, y0) и если эти производные непрерывны в самой точке (x0, y0), тофункция z=f(x, y) дифференцируема в точке (x0, y0). Частные производные. Множество точек М, которые удовлетворяют неравенству (М;М)<, называют -окрестностью точки М.Пусть функция двух переменных z=f(x;у) (для большего количества переменных всё аналогично) определена в некоторой окрестности точки М (x;у). Дадим переменной х приращение так, чтобы точка (х+;у) принадлежала этой окрестности. При этом функция z=f(x;у) изменится на величину,которая называется частичным приращением функции z=f(x;у) по переменной х.Аналогично величину называют частичным приращением функции по переменной у.Если существует предел,то его называют частной производной функции z=f(x;у) в точке М (x;у) по переменной х
|
39,26,31 |
|
||||||
|
2) Обозначим через (М;М) расстояние между точками М и М. Если п=2, М(х;у), М(х;у), то(М;М)=. В п-мерном пространстве(М;М)=. Пусть на множестве D задано функцию и=f(М). Число А называется пределом функции и=f(М) в точке М, если для произвольного числа >0 найдётся такое число >0, что для всех точек М D, которые удовлетворяют условию 0<(М;М)<, выполняется неравенство. Заметим, что если предел существует, то он не должен зависеть от пути, по которому точка М стремится к точке М. Функция и=f(М) называется непрерывной в точке М, если= f(М).Функция и=f(М) называется непрерывной на множестве D, если она непрерывна в каждой точке МD.Точки, в которых непрерывность функции нарушается, называются точками разрыва функция. Точки разрыва могут быть изолированными, создавать линии разрыва, поверхности разрыва и т. д. Например, функция z= имеет разрыв в точке (0;0), а функция z= имеет разрыв на параболе
|
|
|
||||||
|
3)Теорема. Пусть u
= f (х, у) задана
в области D и пусть х = х(t
) и у = у(t
) определены
в области
|
|
|
||||||
|
4)
Пусть в некоторой области D задана
функция
|
|
|
||||||
|
5) Пусть в трехмерном пространстве поверхность S задана уравнением z=f(x, y), где f(x, y) – функция, непрерывная в некоторой области D и имеющая там частные производные по x и по y. Выясним геометрический смысл этих производных в точке M0(x0, y0)∈D, которой на поверхности z=f(x, y) соответствует точка N0(x0, y0, f(x0, y0)). При нахождении частной производной ∂z/∂ x в точке М0 мы полагаем, что z является только функцией аргумента x, тогда как аргумент y сохраняет постоянное значение y=y0, то есть z=f(x, y0)=f1(x).
|
|
|
||||||
|
6)частные
производные
Пусть f(x,
y) —
функция двух переменных x,
y,
определена в некоторой окрестности
точки (x0,
y0).
Если существует конечный предел Дифференциал
Пусть
функция двух независимых переменных
u = f (х, у)
имеет частные производные: Это,
в свою очередь, снова функции двух
переменных, которые снова можно
дифференцировать, и определяются эти
новые производные по той же схеме.
Например:
Обозначение
производных второго порядка:
Последние две производные называются смешанными. Теорема (о
равенстве смешанных производных).
Пусть имеем функцию f (х, у).
Если в окрестности точки M0 (x0,
y0) существуют
смешанные производные
|
|
|
||||||
|
7) Неявные функции многих переменных.Определение. Неявная функция, заданная уравнением F(x1,x2,…,xn,y)=0 (или кратко F(x,y)=0) определяется, как функция y=f(x)=f(x1,x2,…,xn) при подстановке которой в уравнение, оно превращается в тождество на некотором множествеF(x1,x2,…,xn, f(x1,x2,…,xn))=0 , или кратко, F(x,f(x))=0 при xD. Теорема 2. Пусть F(x,y)
имеет непрерывные частные производные
первого порядка в окрестности U(M0)
точки M0(x0,y0), x0= F(M0)=0,
Тогда существует окрестность U(x0) и единственная функция, определенная в этой окрестности y = f(x), такая, что x U(x0) : F(x,f(x))=0 и y0 = f(x0). Эта функция дифференцируема в точке x0 и ее производные определяется по формуле
|
|
|
||||||
|
8)
Теорема (необходимое
условие экстремума).
Пусть функцияf(x:y),
определенная в окрестности точки
Тогда,
для того, чтобы функция имела в
Теорема
(достаточное условие экстремума для
функции 2-х переменных).
Пусть функция
Функции
|
|
|
||||||
|
9)
Метод наименьших квадратов является
одним из наиболее распространенных
и наиболее разработанных вследствие
своей простоты
и эффективности методов оценки
параметров линейных эконометрических
моделей.
Вместе с тем, при его применении следует
соблюдать определенную осторожность,
поскольку построенные с его использованием
модели могут не удовлетворять целому
ряду требований к качеству их параметров
и, вследствие этого, недостаточно
“хорошо” отображать закономерности
развития процесса Рассмотрим процедуру оценки параметров линейной эконометрической модели с помощью метода наименьших квадратов более подробно. Такая модель в общем виде может быть представлена уравнением (1.2): yt = a0 + a1 х1t +...+ an хnt + εt . Исходными данными при оценке параметров a0 , a1 ,..., an является вектор значений зависимой переменной y = (y1 , y2 , ... , yT )' и матрица значений независимых переменных
в
которой первый столбец, состоящий из
единиц, соответствует коэффициенту
модели Название свое метод наименьших квадратов получил, исходя из основного принципа, которому должны удовлетворять полученные на его основе оценки параметров: сумма квадратов ошибки модели должна быть минимальной.
|
|
|
||||||
|
10)
Теорема 1.
Если
|
|
|
||||||
|
11)
Свойство
1. Производная
от неопределённого интеграла равна
подынтегральной функции, то есть если
Свойство
2. Дифференциал
от неопределённого интеграла равен
подынтегральному выражению Свойство 3. Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной константы
Свойство
4. Неопределённый
интеграл от суммы функций равен сумме
неопределённых интегралов Свойство 5. Неопределённый интеграл от разности функций равен соответствующей разности неопределённых интегралов
Свойство
6. Постоянный
множитель можно выносить за знак
интеграла
Свойство
7. Если
|
|
|
||||||
|
12)
|
|
|
||||||
|
13 Свойство инвариантности формул интегрирования Всякая
формула интегрирования (см. таблицу)
сохраняет свой вид при подстановке
вместо независимой переменной любой
дифференцируемой функции, то есть
если Так,
например, если
|
|
|
||||||
|
14)
Замена
переменной в неопределенном интеграле
производится с помощью подстановок
двух видов:
а) |
|
|
||||||
|
15) Пусть u = u(x) и v = v(x) суть две дифференцируемые функции, заданные на одном и том же промежутке [a, b]. Тогда на этом промежутке будет (uv)' = u'v + uv'.Последнее равенство можно переписать в равносильной форме
Отсюда, замечая, что u'dx = du, v'dx = dv, получаем:
причем
произвольная постоянная, находившаяся
в правой части, включена в интеграл
|
|
|
||||||
|
16) Универсальная тригонометрическая подстановка Рассмотрим
интеграл вида С
помощью подстановки
И
так какx =
2·arctg t, то sinx, cosx, dx выражаются рационально через t и dt. Так как рациональная функция от рациональных функций есть рациональная функция, то, подставляя полученные выражения в интеграл (6.1), получим интеграл от рациональной функции
|
|
|
||||||
|
|
|
||||||
|
18)
Задача
о пройденном пути.
Требуется найти путь, пройденный
движущейся по прямой точкой за отрезок
времени
|
|
|
||||||
|
19)
Линейность интеграла. Пусть
Действительно,
если при фиксированном размеченном
разбиении составить интегральную
сумму
В
самом деле, будем при раздроблении
промежутка [a, b]
на части включать c в
число точек деления. Если c = xm,
то + Теорема 2. Пусть функция f(x) непрерывна в промежутке [A, B]. Если a, b, c суть точки этого промежутка, то
В самом деле, если из точек a, b и c две (а тем более три) совпадают, то равенство (13) очевидно. Пусть же все эти точки различны. Если a < c < b, то дело сводится к теореме 3. Прочие случаи взаимного расположения точек a, b, c тоже легко свести к той же теореме. Пусть, например, c < b < a. Тогда
и остается дважды применить формулу
|
|
|
||||||
|
20)
Пусть функция f(x) непрерывна на
[a, b], тогда
21)
Формула Ньютона-Лейбница.
Пусть
функция y
= f(x) непрерывна
на отрезке [a;
b] и F(x) -
одна из первообразных функции на этом
отрезке, тогда справедливо равенство |
|
|
||||||
|
22) Интегрирование по частям является методом преобразования интеграла специального вида
Многократное применение вышеприведённой формулы интегрирования по частям к интегралу вида
приводит к обобщённой формуле интегрирования по частям
|
|
|
||||||
|
23)
Пусть
функция y = f(x)
определена и интегрируема на произвольном
отрезке [а, t],
т.е. функция определена для произвольного значения t ≥ a. Несобственным интегралом (интегралом первого рода) от функции f(x) на полуинтервале [а, +∞) называется предел
Если предел, стоящий в правой части равенства (9.1), существует и конечен, то несобственный интеграл называется сходящимся (к данному пределу), в противном случае — расходящимся. Выделяют следующие две задачи: а) исследование вопроса о сходимости заданного несобственного интеграла; б) вычисление значения интеграла в случае, если несобственный интеграл сходится. В некоторых случаях решения этих двух задач удается объединить. По аналогии с (9.1) определяется несобственный интеграл на полуинтервале (-∞, b]:
Определение
сходимости интеграла
Интеграл |
|
|
||||||
|
24)Пусть функция y = f (x) непрерывна, но не ограниченая на полуинтервале [a, b). Определение. Если существует и конечен предел
где
δ > 0, то он называется несобственным
интегралом (несобственным интегралом
второго рода) от функции y = f (x)
на [а, b)
и обозначается
В этом случае данный несобственный интеграл (9.5) называется сходящимся, в противном случае — расходящимся. Аналогично вводится понятие несобственного интеграла от функции y = f(x) непрерывной, но неограниченной на (а, b]:
|
|
|
||||||
|
25)
Теорема 1 (Первый признак сравнения).
Если
функции Теорема
2 (Второй признак сравнения).
Если
функции |
|
|
||||||
|
26) |
|
|
||||||
|
27)
Если
граница фигуры задана
параметрическими уравнениями
:
|
|
|
||||||
|
28)
На плоскости можно рассмотреть полярную
систему координат Фигура
на плоскости, ограниченная лучами Итак, если предел интегральной суммы, построенной по указанной процедуре, существует, то площадь криволинейного сектора можно вычислить по формуле
|
|
|
||||||
|
29)
Если 2. Находим объем согласно формуле (1). Замечание. Аналогично
вычисляются объемы тел, если известны
площади сечения плоскостями,
перпендикулярной оси
|
|
|
||||||
|
30)
Укажем общий способ вычисления
объемов тел
вращения.
В частности, вычислим объем шара и его
частей.
Пусть криволинейная трапеция, то есть фигура, ограниченная осью Ox, прямыми x = a, x = b и графиком непрерывной возрастающей неотрицательной функции y = f (x), вращается вокруг оси Ox (рис. 7.2.1), вследствие чего образуется тело вращения. Сечение этого тела плоскостью, перпендикулярной оси Ox, есть круг или точка. На промежутке (a; b) выберем точку x. Сечение, проведенное через эту точку перпендикулярно оси Ox, есть круг площадью S (x) = πf 2 (x). Объем части тела вращения, ограниченной сечениями, проведенными через точки a и x, обозначим через V (x), а объем данного тела вращения – через V. Теорема1 Объем тела вращения равен
Теорема2
Объем
шара равен
|
|
|
||||||
|
31) |
|
|
||||||
|
32) Вычисление площадей и длин дуг кривых в декартовых координатах. Пусть
на плоскости Пусть
на отрезке
|
|
|
||||||
|
33) Вычисление площадей и длин дуг кривых в полярных координатах. Когда
кривая, ограничивающая область, задана
в полярных
координатах Если
кривая, ограничивающая область, задана
в полярных координатах
|
|
|
||||||
|
34) Пусть кривая АВ задана уравнением y = f (x), а ≤ х ≤ b, и пусть функция y = f (x) неотрицательна и непрерывна вместе со своей первой производной на отрезке [а, b]. Тогда поверхность, образованная вращением кривой АВ вокруг оси ОХ, имеет площадь S, которая может быть вычислена по формуле
Разобьем
кривую АВ на n частей
точками А = А 0, A 1, A 2,
…, A i -
1, A i,
…, An = B.
Длину частичной дуги A i -
1Ai обозначим
через Δ l = l i − l i -
1.
Заменим кривую ломаной с указанными
вершинами. При вращении ломаной вокруг
оси Ох получим
поверхность, составленную из nбоковых
поверхностей усеченных конусов.
Площадь боковой поверхности i-го
усеченного конуса равна произведению
длины окружности 2··R ( R равно
полусумме радиусов верхнего и нижнего
оснований конуса) на длину образующей
(хорды А i -
1А i).
Поэтому, если положить R = y(ξ i ), x i -
1 ≤
ξ i ≤ x i,
и считать длину хорды Аi -
1 Ai,
равной Δ li,
то получим, что площадь Si боковой
поверхности вращения приближенно
равной Si ≈ 2 π y(ξi) Δ li. Площадь
всей поверхности вращения приближенно
равна сумме площадей частичных
поверхностей Si т.е. Эта
сумма является интегральной суммой.
Так как функция у (x)
непрерывна на [0, L],
то предел этой суммы при существует и равен определенному интегралу от функции у(x) по l. Следовательно,
Или
Перейдем
в интеграле от переменной интегрирования l к
переменной х.
Эти переменные связаны формулой Если l = 0, то х = а, если l = L, то х = b. А так как
окончательно получим
КРИВИЗНА
ПЛОСККОЙ КРИВОЙ.Пусть
плоская кривая C задана
параметрически радиус-вектором
Кривизну кривой можно определить как отношение угла поворота касательной Δφ к длине пройденной дугиΔs = MM1. Такое отношение Δφ/Δs называется средней кривизной дуги кривой. Когда точка M1 приближается к точке M, мы получаем кривизну кривой в точке M:
Ясно,
что кривизна k в
общем случае может быть как положительной,
так и отрицательной, в зависимости от
направления вращения касательной.
Если
кривая задана своим радиусом вектором
где
Если плоская кривая задана явной функцией y = f(x), кривизна кривой вычисляется по формуле
В случае, когда кривая задана в полярных координатах в виде ρ = ρ(φ), ее кривизна k будет определяться выражением
Под кривизной кривой часто понимается абсолютное значение кривизны, без учета направления вращения касательной. В таком случае приведенные выше формулы остаются верными, но в числителе появляется модуль. Например, формула кривизны при параметрическом задании координат кривой x(t) и y(t) будет выглядеть так :
Величина, обратная кривизне, называется радиусом кривизны:
Окружность с таким радиусом и центром, расположенном на главной нормали, будет наилучшим образом аппроксимировать плоскую кривую в данной точке (рисунок 2).
|
|
|
||||||
|
35)
Числовой
ряд –
это сумма членов числовой последовательности
вида
Обозначение:
|
|
|
||||||
|
36) Геометрический ряд. Так называется ряд (бесконечная сумма), члены которого образуют геометрическую прогрессию с первым членом а0 и знаменателем прогрессии, равным q. Если |q| <
1, то
существует предел суммы n первых
членов этой прогрессии при неограниченном
увеличении количества этих членов n:
В этом случае говорят о бесконечно убывающей геометрической прогрессии.
|
|
|
||||||
|
37) Линейная комбинация рядов
Если
ряды
Группировка членов ряда
Сгруппируем
слагаемые ряда Перемножение рядов
Пусть
имеются два ряда
|
|
|
||||||
|
38)
|
|
|
||||||
|
39) |
|
|


 ,
имеет в точке
,
имеет в точке
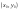 частные производные
частные производные
 и
и
 .
. локальный экстремум, необходимо, чтобы
все частные производные в этой точке
обращались в ноль.
локальный экстремум, необходимо, чтобы
все частные производные в этой точке
обращались в ноль. определена и непрерывна вместе со
всеми своими частными производными
до второго порядка включительно в
окрестности точки
определена и непрерывна вместе со
всеми своими частными производными
до второго порядка включительно в
окрестности точки
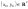 ,
и пусть
,
и пусть
 - критическая точка функции
- критическая точка функции
 .Тогда,
если в тейлоровском разложении
.Тогда,
если в тейлоровском разложении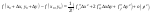
 в точке
в точке
 квадратичная форма
квадратичная форма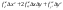 положительно
определена, то в точке
положительно
определена, то в точке
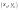 функция имеет локальный минимум, если
отрицательно определена, то локальный
максимум, если же квадратичная форма
принимает значения разных знаков, то
экстремум отсутствует.
функция имеет локальный минимум, если
отрицательно определена, то локальный
максимум, если же квадратичная форма
принимает значения разных знаков, то
экстремум отсутствует.
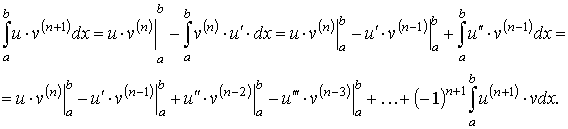

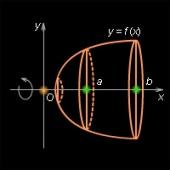
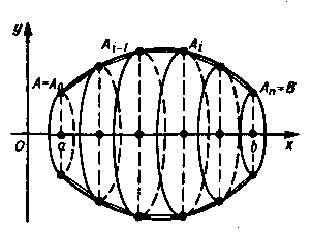
 рис1
рис1 рис2
рис2