
- •9. Несобственные интегралы. Признаки сравнения.
- •10. Несобственные интегралы c особенностями в нескольких точках.
- •11. Функции многих переменных
- •17. Свойства функций, непрерывных на замкнутом промежутке
- •18. Понятие локального экстремума. Необходимые условия.
- •19.Достаточные условия локального экстремума.
- •№27. Численные методы вычисления определённого интеграла
19.Достаточные условия локального экстремума.
Т.Пусть
ф-ция z=f(x,y)
диф-ма в т.
![]() (
(![]() )
и имеет вторые производные в этой
точке,т.
)
и имеет вторые производные в этой
точке,т.![]() -стационарная.Обозначим
-стационарная.Обозначим![]() Тогда
Тогда
1)если
![]() ,то
в т.
,то
в т.![]() -лок.экстремум.
При этом
-лок.экстремум.
При этом
![]()
![]() -лок.max,
-лок.max,![]()
![]() -лок.min
-лок.min
2)если
![]() ,то
в т.
,то
в т.![]() лок.экстремума нет.
лок.экстремума нет.
3)если D=0,то требуется доп.исследования.
Док-во:Разложим
f(x,y)по
формуле Тейлора в окр-ти т.M0:
Т.к.
![]() -стац.
Точка,первый диф-ал=0
-стац.
Точка,первый диф-ал=0![]()
Остается

![]() квадратичная
форма от
квадратичная
форма от
![]()
Если
![]() -положит.определена
(по критерию Сильвестра)
-положит.определена
(по критерию Сильвестра)
![]() в
т.
в
т.
![]() -лок.min
-лок.min
Если![]() отриц.определена
отриц.определена![]() в
т.
в
т.![]() -лок.max
-лок.max
№20.Понятие неявной ф-ции.Теорема существования и непрерывности неявной ф-ции.Дифференцирование неявной ф-ции.Диф-ие неявной ф-ции нескольких переменных.
Опр.Неявная
ф-ция y=f(x)-это
решение ур-ия F(x,y)=0
относительно y,т.е.
![]()
![]()
Т.(существование и непрерывность неявной ф-ции)
Пусть выполн. усл.:
1)F(x,y)
непр. в прямоуг. Q={(x,y)|a<x<b,c![]() y
y![]() d}
d}
2)![]()
![]() (т.е.
на нижних и верхних сторонах прямоугольникаQ
ф-ция имеет знач. разных знаков)
(т.е.
на нижних и верхних сторонах прямоугольникаQ
ф-ция имеет знач. разных знаков)
3)
![]()
![]() явл.
строго монотонной ф-цией относит.y
на [c,d].Тогда
на (a,b)
явл.
строго монотонной ф-цией относит.y
на [c,d].Тогда
на (a,b)
![]() !
неяв. ф-цияy=f(x),определяемая
ур-ем (*) и эта ф-ция непр. на (a,b)
.
!
неяв. ф-цияy=f(x),определяемая
ур-ем (*) и эта ф-ция непр. на (a,b)
.
Т.(диф-ть неяв. ф-ции)
Пусть:1)F(x,y)диф-ма
в некоторой окр. точки
![]() ,
,![]()
![]()
2)![]() непр.
в т.
непр.
в т.![]()
3)![]()
Тогда
сущ.прямоугольник
 ,в
к-ом ур-иеF(x,y)=0
определяет единственную неявную ф-цию
y=f(x),где
,в
к-ом ур-иеF(x,y)=0
определяет единственную неявную ф-цию
y=f(x),где
![]() и произв. Неявной ф-ции ищется по формуле:
и произв. Неявной ф-ции ищется по формуле:
![]()
Замечание.
При
вычислении
![]() сначала
берется частная производная поx,а
затем вместо y
подставляется ф-ция f(x).Следствие:Если
ф-ция F(x,y)
диф-ма n
раз в окр.т.
сначала
берется частная производная поx,а
затем вместо y
подставляется ф-ция f(x).Следствие:Если
ф-ция F(x,y)
диф-ма n
раз в окр.т.
![]() ,то
и неяв.ф-цияy=f(x)диф-ма
n
раз в окр-ти т.
,то
и неяв.ф-цияy=f(x)диф-ма
n
раз в окр-ти т.
![]() .
.
![]()
Теорема.(диф-ть
неяв. ф-ции нескольких переменных)
Пусть:1)![]() диф-ма
в нек. точке
диф-ма
в нек. точке![]()
![]()
2)![]() непр.
в
непр.
в![]() ;
;
3)![]()
Тогда
в окр.т.
![]() ур-ие
ур-ие![]() опр-ет единств. неяв. ф-цию
опр-ет единств. неяв. ф-цию![]() ,причем
,причем![]() неяв.ф-ция
диф-ма в окр. т.
неяв.ф-ция
диф-ма в окр. т.![]() и ее частные производ. Вычисл по формулам:
и ее частные производ. Вычисл по формулам:
![]() для
всех i=1,2,…m.
для
всех i=1,2,…m.
№21. Неявные функции, определяемые системой уравнений.
Рассм: Решение:


называется совокупностью неявных функций, определяемых системой уравнений.
Определитель
 ,
,
сост
частных произв назыв определителем
Якоби, или якобианом ф-ий
![]() ,
,![]() ,
…,
,
…,![]() по переменным
по переменным![]() ,
,![]() ,
…,
,
…,![]() и обознач
и обознач![]() .
.
Теорема(диф-ть неяв ф-й заданных сист ур-й). Пусть
функции
 ,
, ,
…,
,
…, из (**) дифф-емы вU
из (**) дифф-емы вU ;
;частные производные

 непрерывны в точке
непрерывны в точке ;
; ,
, ,…,
,…, ,
, .
.
Тогда
определена единственная совокупность
неяв ф-ий, дифф-емых в U
![]() и
частные производные неявных ф-ий
находятся по след системе:
и
частные производные неявных ф-ий
находятся по след системе:
Из
этой системы однозначно опред частные
произв для
![]() ,
,![]() (Она определена и сущ единств реш-е.)
(Она определена и сущ единств реш-е.)
№22. Касательная плоскость и нормаль к поверхности, заданной явными и неявными функциями.
Касательной плоскостью к пов-ти в т М назыв плоскость, в которой лежат все касательные в т М к различным кривым, проведённым на пов-ти через эту точку.
Нормалью к пов-ти назыв перпендикуляр к касательной плоскости в точке касания.
Если ур-е пов-ти в декартовой системе координат задано в явной форме z=f(x,y), где f(x,y) – дифференцируемая ф-я, то уравнение касательной плоскости в точке поверхности М0(x0,y0,z0) есть.
Z-z0=f’x(x0,y0)(X-x0)+f’y(x0,y0)(Y-y0)+f’y(x0,y0)(Y-y0). Здесь z0=f0(x0,y0), а X,Y,Z – текущие коорд точки касательной плоскости.
Уравнения нормали имеют вид:
(X-x0)/f’x(x0,y0)=(Y-y0)/f’y(x0,y0)=(Z-z0)/-1
где X,Y,Z – текущие координаты точки нормали.
Если ур-е пов-ти задано в неявной форме F(x,y,z)=0 и F(x0,y0,z0)=0, соотв ур-я будут иметь такой вид:
F’x(x0,y0,z0) (X-x0)+ F’y(x0,y0,z0) (Y-y0)+ F’z(x0,y0,z0) (Z-z0)=0 – ур-е касательной плоскости
(X-x0)/F’x(x0,y0,z0)=(Y-y0)/F’y(x0,y0,z0)=(Z-z0)/ F’z(x0,y0,z0) – ур-е нормали.
Пример: ур-е касательной и нормали к пов-ти z=x2/2-y2 в т. М(2;-1;1)
Найдём част произв и их знач в т. М: (dz/dx)M=2, (dz/dy)M=2. Подставить в 1 и 2 формулы и имеем 2x+2y-z-1=0 (ур-е кас плоскости) и (x-2)/2=(y+1)/2=(z-1)/-1 (ур-е нормали).
№23.Понятие кратного интеграла. Геометрический смысл двойного интеграла. Свойства.
Опр. Кратным интегралом от функции f на множестве D называется предел интегральной суммы, когда максимальный диаметр разбиения 0.
![]()
![]()

Двойной
интеграл от f(x;y)
на
![]() :
:
![]()
Геометрический смысл двойного интеграла:
Это объем тела, ограниченного сверху непрерывной поверхностью z=f(x,y), а снизу плоскостью z=0.
Свойства кратных интегралов:
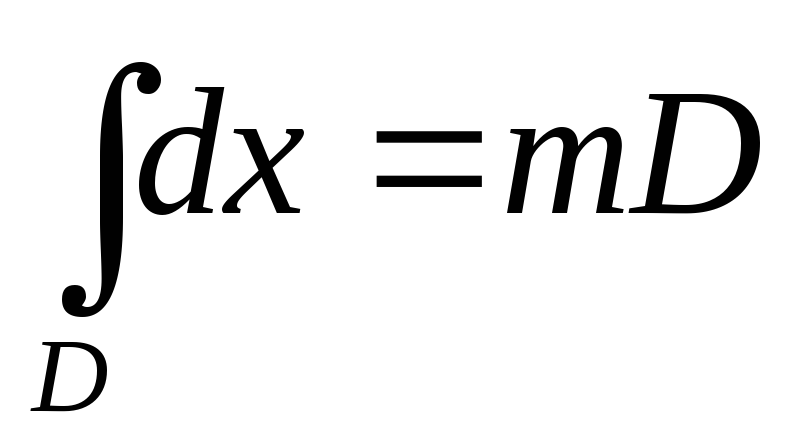 ,
,
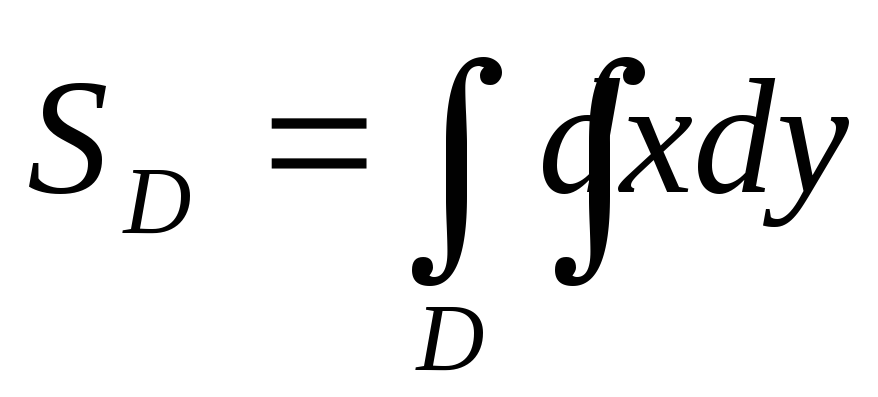
 (Площадь)
(Площадь) (Объем)
(Объем) ,
где A,B=const.
,
где A,B=const. -
мн-во
меньшей размерности
-
мн-во
меньшей размерности

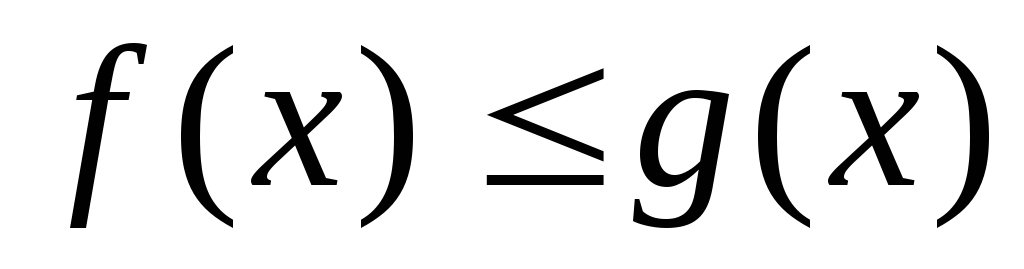 на
D
=>
на
D
=>


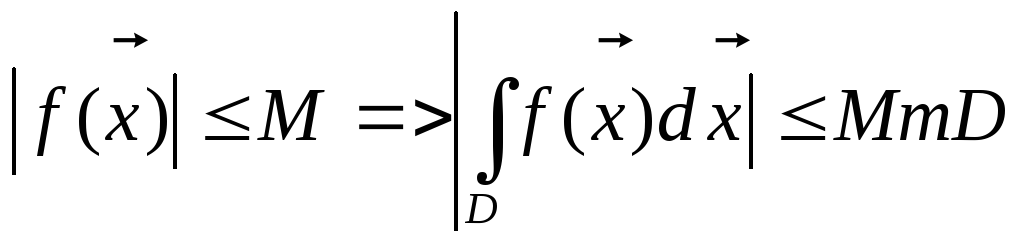 ,
M=const
,
M=constТеорема о среднем значении: Пусть
 непрерывна
на замкнутом мн-веD.
Тогда
непрерывна
на замкнутом мн-веD.
Тогда
 ;
;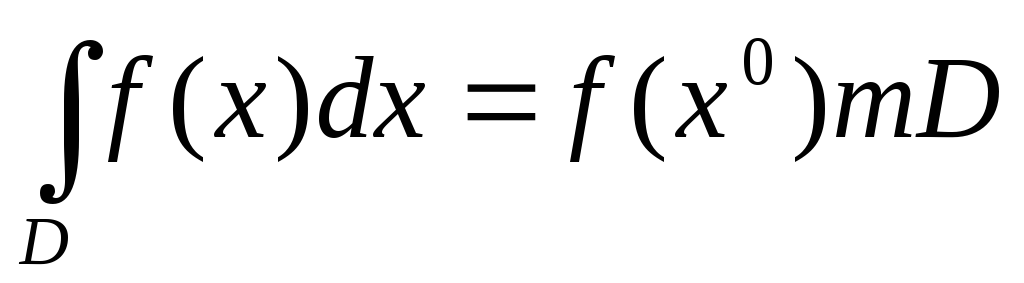 .
.
№24. Вычисление кратного интеграла путем сведения к повторным.
Сведение кратного интеграла к повторным.
Теорема:
Пустьf(x,y) заданна и непрерывна на прямоугольнике
![]()
Тогда
![]()
![]() непрерывна
на [a;b]
непрерывна
на [a;b]
Доказательство:
![]() ;
;
![]() , при |h|<
, при |h|<![]() ;
;
Тогда
![]() .
.
Теорема:
Пусть
f(x,y)
определена и непрерывна на прямоугольнике
![]()
Тогда
![]()
№25. Замена переменных в кратном интеграле.
Пусть x=(u,v), y=(u,v). Функции и имеют непрерывные производные в замкнутой ограниченной области D
I(u,v)=![]() ≠0
≠0
Тогда
![]()
D→D’ (выраж. В переменных u,v)
Пусть
x=(u,v,w),
y=(u,v,w),
z=![]() (u,v,w)
(u,v,w)

Тогда:
![]() №26.
Несобственные кратные интегралы
№26.
Несобственные кратные интегралы
1) Интеграл по бесконечной области
Пусть f(x,y), непрер. в бесконечной области D:
![]() ,
где D’
– конечная область, лежащая в D,
которая расширяется произвольным
образом.
,
где D’
– конечная область, лежащая в D,
которая расширяется произвольным
образом.
Если существует конечный предел, независ. От выбора области D’ и способа расширения, то несобственный интеграл называется сходящимся.
2) Интеграл от разрывной функции
Пусть f(x,y) непрер. В ограниченной замкн. D всюду, за исключением P0(x0, y0)
Если
существует конечный предел ![]() ,
где D
-
область D
с вырезанной -окрестностью
т. P0,
то этот предел называется несобственным
интегралом от f(x,y)
по области D
,
где D
-
область D
с вырезанной -окрестностью
т. P0,
то этот предел называется несобственным
интегралом от f(x,y)
по области D
Интеграл Пуассона
![]()
Переход к полярным координатам
![]()
![]()
![]()
![]()
![]()
![]()
