
Матем_лекции_ 1сем_гр.,2621,2721
.pdf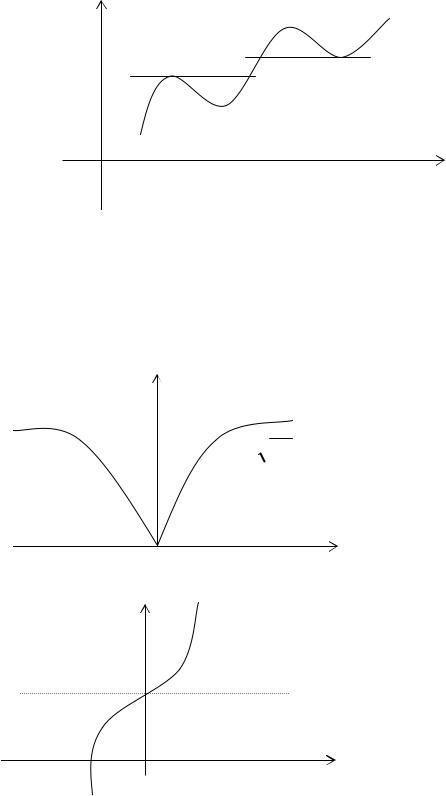
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
y
max |
min |
0 |
x |
Если в точке x0 дифференцируемая функция имеет экстремум, то в некоторой окрестности этой точки выполнены условия теоремы Ферма. Следовательно, f x0 0. Но функция может
иметь экстремум и в точках, в которых она не дифференцируема.
Отсюда необходимое условие экстремума: для того, чтобы функция y= f(x) имела экстремум в точке x0 , необходимо, чтобы её производная в этой точки равнялась нулю или не существовала.
(Экстремум в точке x =0, но функция здесь не дифференцируемая) (Производная равна нулю при x=0, но экстремума нет)
y
y 3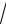 x2
x2
x
1 y x3 1
x
Точки в которых выполнено необходимое условие экстремума, называются критическими (стационарными). Их также называют точками, подозрительными на экстремум. Одна критическая точка вовсе не обязательно является точкой экстремума.
Таким образом, для нахождения экстремумов функции требуется дополнительное исследование критических точек, т.е. нужно достаточное условие экстремума.
Теорема (первое достаточное условие экстремума). Если при переходе через точку x0
производная дифференцируемой функции меняет свой знак с плюса на минус, то точка x0 есть точка максимума функции y=ƒ(x), а если с минуса на плюс, то точка минимума .
61
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
Схема исследование функции y=ƒ(x) на экстремум:
1.Найти f x .
2. |
|
или не существует. |
Найти критические точки функции, в которых f x =0 |
3.Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции.
4.Найти экстремумы функции (экстремальные значение функции).
Пример 5. Исследовать функцию у х х 1 3 |
на экстремум. |
Теорема (второе достаточное условие экстремума). Если функция у=ƒ(x) дважды |
|
дифференцируема и в некоторой точке x0 f x0 =0, |
f x0 >0, то x0 есть точка минимума функции |
y=ƒ(x),если f x0 =0, f x0 <0, то точка максимума.
Для отыскания наибольшего и наименьшего значений функции на отрезке надо найти значения функции в критических точках и на концах отрезка и выбрать из них наименьшее ƒmin и наибольшее значение ƒmax.
y y
0 |
a |
b x |
a |
b |
x |
Если функция непрерывна на интервале (а,b), то она может не принимать на нем наибольшего и наименьшего значений. В частности, если дифференцируемая функция на интервале (а,b) имеет лишь одну точку максимума, то наибольшее значение функции совпадает с максимумом этой функции.
Пример 6. Найти наибольшее и наименьшее значения функции у = х3 – 12х на отрезке [0,
5].
Решение. Сначала найдем производную функции: у’ = 3х2 – 12.
Затем найдем критические точки, т.е. точки, в которых у’ = 0 или не существует: 3х2 – 12 = 0, откуда критические точки х1 = –2, х2 = 2. Точка х1 = –2 не принадлежит отрезку [0, 5], поэтому мы исключаем ее из рассмотрения.
Вычислим значения функции в критической точке х2 = 2 и на концах интервала и выберем из них наибольшее и наименьшее: у(2) = – 16, у(0) = 0, у(5) = 65.
Ответ: Т.о. наибольшее значение функции на отрезке [0, 5] равно 65, наименьшее равно –16.
9.3. Исследование функции на выпуклость и точки перегиба
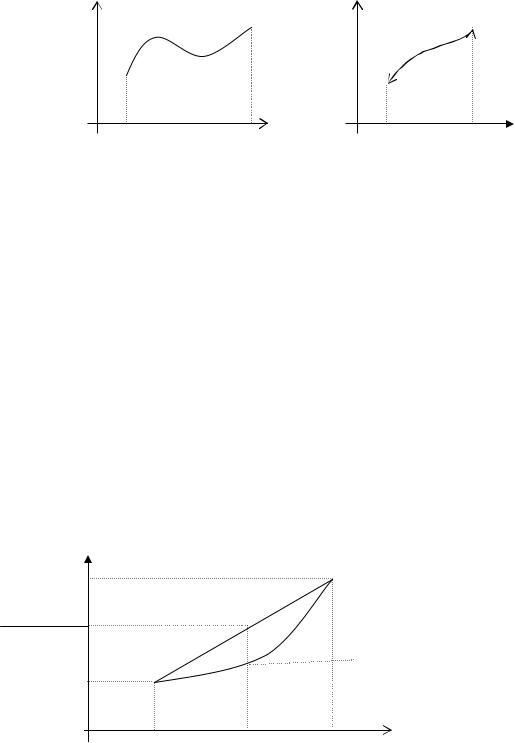
Функция y=ƒ(x) называется выпуклой вниз на промежутке X,если для x1,x2ЄX |
|||||||||
x x |
2 |
|
|
f x |
f x |
2 |
|
||
f |
1 |
|
|
1 |
|
|
|
||
2 |
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
||
y
f x2 |
|
|
выпуклость вниз |
f x1 f x2
2
|
x x |
2 |
|
|
f x |
f x |
2 |
|
|
|
f |
1 |
|
|
1 |
|
|
||
|
2 |
|
|
2 |
|
|
|||
f x1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
62
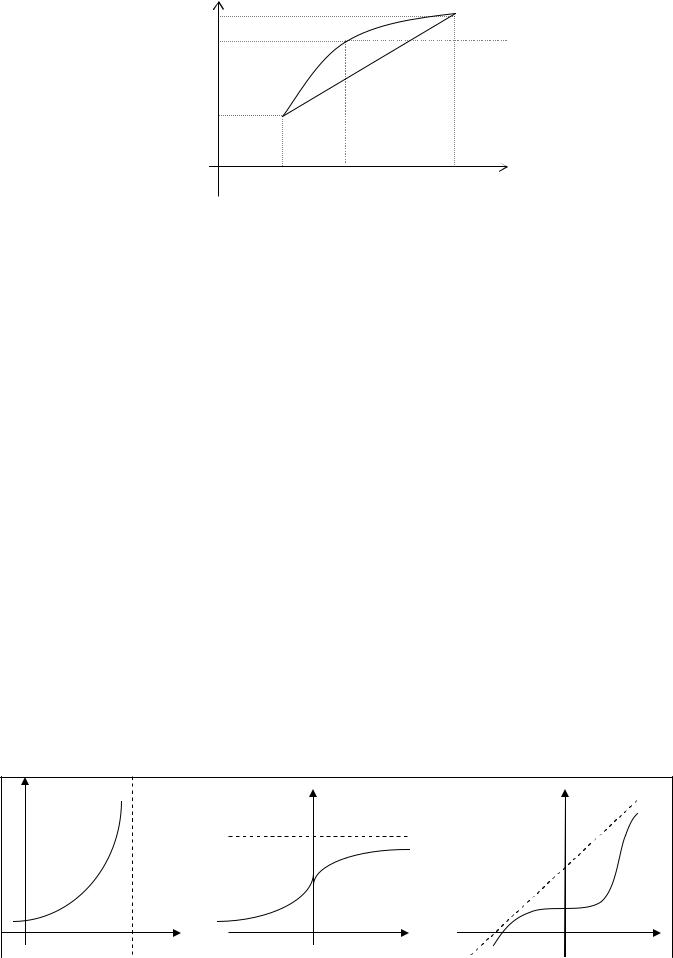
y f x1
f x1
выпуклость вверх
Generated by Foxit PDF Creator © Foxit Software http://www.foxitsoftware.com For evaluation only.
x x |
2 |
|
|
f x f x |
2 |
|
|
f |
1 |
|
|
1 |
|
||
2 |
|
2 |
|
|
|||
|
|
|
|
|
|
||
x
Функция y=ƒ(x) называется выпуклой вверх на промежутке X, если для x1,x2ЄX
x x |
2 |
|
|
f x f x |
2 |
|
|
f |
1 |
|
|
1 |
|
||
2 |
|
2 |
|
|
|||
|
|
|
|
|
|
||
Теорема. Функция выпукла вниз (вверх) на промежутке X тогда и только тогда, когда её 1- ая производная на X монотонно возрастает (убывает ).
Теорема. Если y=f(x) дважды дифференцируема а, f``(x)> 0 (f``(x)<0) внутри некоторого промежутка X, то функция выпукла вниз (вверх) на этом промежутке .
Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла вниз и вверх.
Отсюда следует, что точка перегиба – это точка экстремума 1- й производной.
Теорема (необходимое условие перегиба). В точке перегиба x0 дважды дифференцируемой функции f```(x)=0.
Теорема.(достаточное условие перегиба). Если 2-я производная дважды дифференцируемой функции при переходе через точку x0 меняет свой знак, то x0 есть точка перегиба.
Замечание. Если критическая точка дифференцируемой функции не является точкой экстремума, то она есть точка перегиба.
Схема исследования функции на выпуклость и точки перегиба:
1.Найти f```(x).
2.Найти точки, в которых f```(x)=0 или не существует.
3.Исследовать знак 2-ой производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости и наличии точек перегиба.
4.Найти значения функции в точках перегиба.
Пример 7. Исследовать функцию у х х 1 3 на выпуклость и точки перегиба.
9.4. Асимптоты графика функции
Асимптотой графика функции y=f`(x) называется прямая, расстояние от которой до точки(x, f`(x)) стремится к нулю при x - .
Асимптоты бывают вертикальные, горизонтальные и наклонные .
у |
у |
у |
y=b |
b |
|
x=a |
|
y=kx+b |
а |
|
|
х |
х |
х |
|
|
|
Теорема. Пусть функция y=f(x) определена в некоторой окрестности точки x0 и хотя |
бы |
|
один из пределов функции при x x0 - 0 или при x x0 +0 равен бесконечности. Тогда прямая x= x0 является вертикальной асимптотой функции y=f`(x).
63

Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
Вертикальные асимптоты x= x0 следует искать в точках разрыва функции y=f(x) или на концах её области определения в (а,b),если а и b - конечные числа.
Теорема. Пусть функция y=f(x) при достаточно больших x и существует конечный предел
lim f x b . Тогда прямая y=b есть горизонтальная асимптота графика функции
x
Теорема. Пусть функция y=f(x) определена при достаточно большой x и существуют
конечные пределы lim |
f x |
k и |
lim f x kx b . Тогда прямая y=kx + b является наклонной |
|||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
|
x |
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
асимптотой функции y=f(x). |
|
|
|
|
|
|
|
|
|
|
a |
b |
|
|
|
|
|
|
|
|||||
|
График дробно-линейной функции у |
ах b |
, где |
c 0, |
|
|
0 , имеет вертикальную |
|||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
c |
d |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
cx d |
|
|
|
|
|
|
|
|
|
|
|||
x |
c |
|
и горизонтальную асимптоты |
y |
a |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
d |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х2 4 |
|
|
|
х2 |
4 |
х3 |
||||
|
Пример 8. Найти асимптоты графиков функций: а) у = |
|
; б) у = |
|
|
; в) у = |
|
. |
||||||||||||||||
|
х2 4 |
х2 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
х2 1 |
||||||
9.4.Общая схема исследования функций и построения их графиков
1.Найти область определения функции.
2.Исследовать функцию на четность и нечетность.
3.Найти вертикальные асимптоты.
4.Исследовать поведение функции в бесконечности, найти горизонтальные и наклонные асимптоты.
5.Найти экстремумы и интервалы монотонности функции.
6.Найти интервал выпуклости функции и точки перегиба.
7.Найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.
Рассмотрим схему исследования функций на следующем примере.
Пример 9. Исследовать функцию у = х2 4 и построить ее график.
х2 4
Решение. 1) Найдем область определения функции.
Областью определения этой функции является вся действительная ось, за исключением двух точек х1 = –2 и х2 = 2, в которых имеет место разрыв (знаменатель х2 – 4 = 0).
2) Исследуем функцию на четность-нечетность.
Функция четная, т.к. у(-х) = |
( х)2 |
4 |
|
х2 |
4 |
= у(х). Четность функции определяет |
|
( х)2 |
4 |
х2 |
4 |
||||
|
|
|
симметрию ее графика относительно оси Оу.
3) Найдем вертикальные асимптоты графика функции.
Вертикальные асимптоты следует искать в точках разрыва функции или на границе ее области определения. Точками разрыва являются х1 = –2 и х2 = 2.
Вычислим пределы функции в окрестностях этих точек.
|
|
|
|
|
x2 |
4 |
|
|
|
|
x2 |
4 |
|
|
|
|
|
||||||
Предел слева |
lim |
|
|
|
|
|
, предел справа lim |
|
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
x 2 0 x2 |
4 |
|
|
|
x 2 0 x2 |
4 |
|
|
|
|
|
||||||||||
|
|
|
|
x2 |
4 |
|
x2 |
4 |
|
|
|
|
|
|
|
|
|
||||||
Аналогично |
lim |
|
|
|
|
|
, lim |
|
|
. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x 2 0 x2 |
4 |
x 2 0 x2 |
4 |
|
|
|
|
|
|
|
|
|
||||||||||
Следовательно, прямые х = –2 и х = 2 являются вертикальными асимптотами функции. |
|
||||||||||||||||||||||
4) Найдем горизонтальные или наклонные асимптоты графика функции. |
|
||||||||||||||||||||||
Для |
этого |
|
|
вычислим |
пределы: |
k |
|
|
f (x) |
|
x2 |
4 |
и |
||||||||||
|
|
lim |
|
lim |
|
|
0 |
||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x |
x x(x2 |
4) |
|
||||
b lim[ f (x) kx] lim |
x2 |
4 |
|
(по формуле y |
|
kx +b) заключаем, |
|
|
|
||||||||||||||
|
|
|
|
1. |
Откуда |
= |
что уравнение |
||||||||||||||||
|
|
|
|
||||||||||||||||||||
x |
x x2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
горизонтальной асимптоты имеет вид: y = 0x +1, т.е. у = 1.
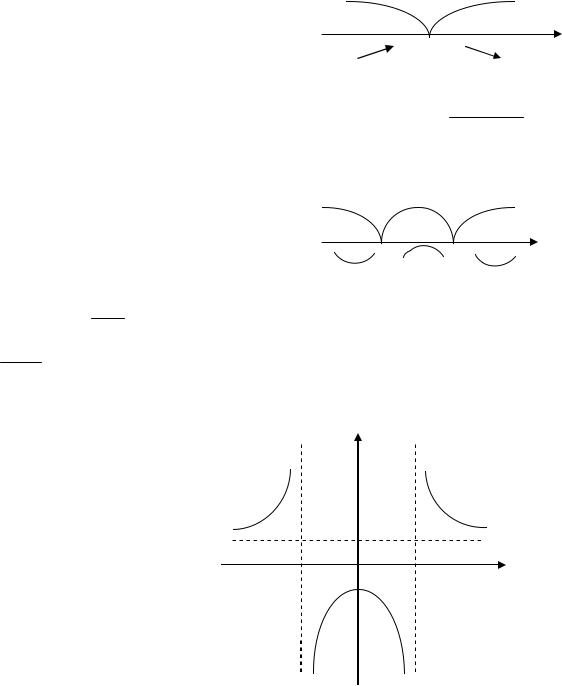
5) Найдем экстремумы и интервалы монотонности.
64
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
Производная заданной функции у’ = |
16х |
|
равна нулю (у’ = 0) при х=0 и не существует |
|
(х2 4) |
2 |
|||
|
|
при х = ±2. Но критической является только точка х=0 (т.к. значения х = ±2 не входят в область определения функции). Поскольку при x < 0 f’(x) > 0, а при x > 0 f’(x) < 0, то х=0 – точка
максимума функции и fmах(x)= |
0 |
4 |
= – 1. |
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
4 |
y' |
+ |
|
|
|
||
На интервалах (-∞; -2) и (-2; 0) |
|
– |
x |
|||||
функция возрастает , на интервалах |
у |
-2 |
0 |
2 |
||||
(0; 2) и (2; +∞) –. убывает |
|
|
|
|
|
|
||
6) Найдем интервалы выпуклости и точки перегиба.
Для этого надо найти вторую производную функции у’’ = 16(3х2 4) . Видно, что у’’ = 0 не
(х2 4)3
имеет действительных корней, и это исключает существование у графика точек перегиба. Вместе с тем по корням знаменателя (-2 и 2) можно установить, что при переходе через эти значения х знаки у’’ меняются.
На интервалах (-∞; -2) и (2; +∞) |
y” + |
– |
+ |
функция выпукла вниз, на интервале |
-2 |
2 |
x |
(-2; 2) – выпукла вверх. |
y |
|
|
7) Найдем точки пересечения с осями координат.
f(0) = 0 4 = – 1, т.е. точка пересечения с осью ординат (0; -1). Уравнение f(х) = 0, (т.е. 0 4
х2 4 = 0), решений не имеет, следовательно, график функции не пересекает ось абсцисс.
х2 4
8)На основании полученных данных построим график заданной функции.
у
|
1 |
|
-2 |
2 |
х |
|
-1 |
|
65

Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
В.10. Дифференциал функции 10.1. Определение дифференциала
Пусть функция y = f(x) определена на промежутке Х и дифференцируема в некоторой окрестности точки х Х. Тогда существует конечная производная
lim y f (x)
x 0 x
На основании теоремы о связи бесконечно малых величин (БМВ) с пределами функций
можно записать |
y |
f |
|
|
|
|
|||
x |
(x) ( x) , где – ( x) БМВ при x 0. |
|||
Откуда |
|
|
|
|
|
|
|
||
|
|
y f (x) x ( x) x . |
|
|
Т.о. приращение функции y состоит из 2 слагаемых: 1) |
линейного относительно x; 2) |
|||
нелинейного (которое является БМВ более высокого порядка малости, чем x)
Определение. Дифференциалом функции называется главная, линейная относительно x часть приращения функции, равная произведению производной данной функции на приращение
независимой переменной |
|
|
|
|
||||||
|
|
|
|
|
|
(1) |
|
|
|
|
|
|
|
|
dy f (x) x |
|
|
|
|
||
|
Дифференциал независимой |
переменной равен |
приращению этой переменной: |
dx = x |
||||||
(т.к. для функции у=х дифференциал будет равен: dy dx x x x ). |
|
|||||||||
|
Поэтому формулу (1) можно записать в виде |
|
|
|
|
(2) |
|
|||
|
dy f (x) dx |
|
|
|||||||
=> f |
|
dy |
(т.е. производная функции есть |
отношение |
дифференциала |
функции к |
||||
|
||||||||||
(x) |
|
|||||||||
dx
дифференциалу независимой переменной).
Пример 9. Найти дифференциал функции у = 6х2 – 3.
Решение. Вычислим производную данной функции у = 12х и подставим в формулу (2): dy 12х dx .
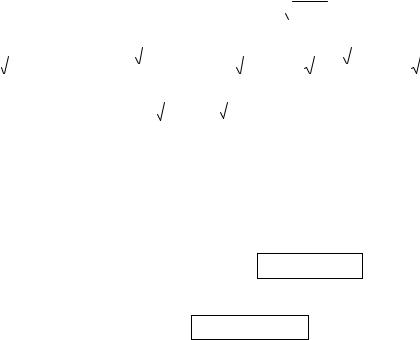
Геометрический смысл дифференциала: Дифференциал функции есть приращение ординаты касательной, проведенной к графику функции y = f(x) в данной точке, когда х получает приращение x.
На рисунке dy = KN, y = M1N.
dy < y |
dy > y |
Свойства дифференциала (1-5 аналогичны свойствам производной):
1.dС = 0.
2.d(Сu) = Сdu.
3.d(u v) =du dv.
4.d(uv) = vdu + udv.
|
u |
|
vdu udv |
|
|
|
|
||
5. |
d |
|
|
|
|
. |
|
|
|
|
v2 |
|
|
||||||
|
v |
|
|
|
|
|
|||
6. |
Свойство инвариантности (т.е. неизменности) формы (формулы) дифференциала. |
||||||||
Рассмотрим сложную функцию y f (u),u (x) . |
|||||||||
Тогда |
|
|
|
|
dy f |
|
, |
||
|
|
|
|
(u) du |
|||||
66
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
т.е. формула дифференциала не изменяется, если вместо функции от независимой переменной х рассматривать функцию от зависимой переменной и.
|
|
10.2. Применение дифференциала в приближённых вычислениях |
|
|
|
|||||||||||||||||||||||||||||||
|
|
Из изложенного выше следует, что y |
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
(x) x ( x) x . Поэтому при достаточно |
|||||||||||||||||||||||||||||||||
малых значениях x у dy или |
f (x x) f |
(x) f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
(x) x . Откуда |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
f (x x) f (x) f (x) x |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
Пример 10. Вычислить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
приближенно, используя дифференциал функции, tg460. |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
Решение. Для приближенных вычислений воспользуемся формулой (3). |
|
|
|
|||||||||||||||||||||||||||||||
|
|
Положим f(x) = tgx. Найдем производную f’(x) |
= (tgx)’ |
= |
|
1 |
|
. Тогда |
|
|
|
|||||||||||||||||||||||||
|
|
cos2 x |
|
|
|
|||||||||||||||||||||||||||||||
tg(x x) tgx |
|
x |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
. Учитывая, что tg46 |
|
= tg(45 |
|
|
+ 1 ) = tg |
|
|
|
|
, возьмем х = |
|
и |
х = |
||||||||||||||||||||
cos2 x |
|
|
|
|
|
|
4 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
180 |
|
|
|||||||||
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
180 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
0 |
|
tg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Тогда tg46 |
|
= tg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 0,0349 1,035 . |
|
|
|
|||||||||
|
|
|
|
|
4 |
|
180 |
|
|
4 |
|
cos |
2 |
|
180 |
|
90 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 11. Вычислить приближенно 4 16,64 ,
16,64 ,
Решение . Приближенная формула для вычисления корней n -й степени :
|
|
|
|
|
|
|
1 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
n |
|
|
|
1 |
|
1 |
x |
|
|
|
4 |
|
|
|
4 |
|
|
x x |
|
4 |
|
|
x |
||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y x; f |
x |
x |
|
|
|
|
, поэтому x x |
|
x |
4x |
|
|
x 1 |
|
. |
||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
nx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,64 |
|
|
|
|
|
|
|
|
|
|
||||
Возьмем x =16; x =0,64 ; 4 16,64 4 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
16 1 |
|
|
|
|
|
2 1,01 2,02 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
4 16
10.3.Дифференциалы высших порядков
Для дифференцируемой функции y = f(x) dy f (x) dx . Если дифференциал независимой переменной dx имеет произвольное, но фиксированное значение, не зависящее от х, то dy - некоторая функция от х, которая также может иметь дифференциал.
Дифференциалом n – го порядка (n – ым дифференциалом) называется дифференциал от дифференциала (n–1)–го порядка данной функции:
d n y d(d n 1 y)
Дифференциал n – го порядка равен произведению производной n – го порядка на n – ю степень дифференциала независимой переменной.
d n y f (n) (x)dxn . (где dxn (dx)n )
=> f |
(п) |
(x) |
d п y |
. В отличие от дифференциала первого порядка дифференциалы более |
|
dxп |
|||
|
|
|
|
высоких порядков не обладают свойством инвариантности формы.
67
