Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Институт экономики, управления и права

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Матем_лекции_ 1сем_гр.,2621,2721

.pdf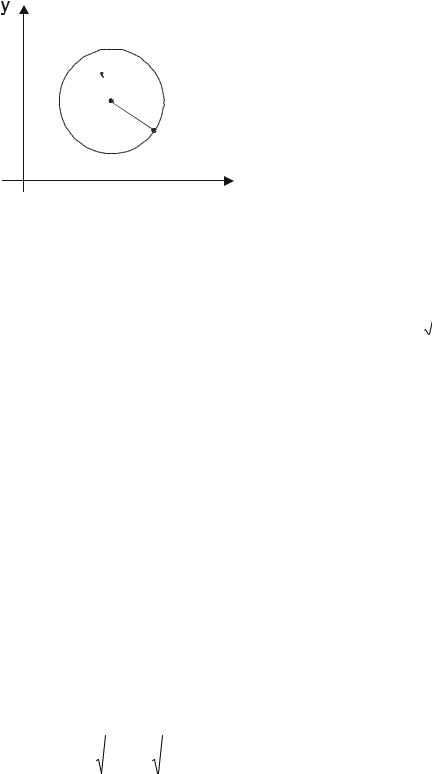

Скачиваний:

Добавлен:

01.06.2015

Размер:

927.18 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com

For evaluation only.

В.3. Уравнения кривых 2-го порядка

3.1. Уравнение окружности

Пусть дана окружность радиуса R с центром в т. О (хо,

уо).

Тогда нормальное уравнение окружности имеет

вид:

О (хо, уо)

(х-хо)2 + (у-уо)2 = R2

(15)

В частности, если центр окружности совпадает с

M(x,y)

началом координат, то уравнение имеет вид:

х2 + у2 = R2

(16)

Рассмотрим уравнение 2-й степени с двумя

переменными в общем виде:

Ах2 + Вху + Су2 + Dx + Ey + F = 0,

(17)

в котором А, В и С не равны нулю одновременно,

т.е. А2 + В2 + С2 0.

Для того, чтобы уравнение (17)

было уравнением окружности, необходимо, чтобы В=0,

А=С 0, т.е.

Ах2 + Ау2 + Dx + Ey + F = 0

(18)

При этом действительная окружность получается, если

D2 + E2 4AF. Центр такой

окружности расположен в точке

, а радиус равен

D2 E2 4AF

;

Уравнение (18) называется общим уравнением окружности.

Если разделить его на А 0 и дополнить члены, содержащие х и у до полного квадрата,

получим уравнение (15): х

D 2
		y

2A

E	2	D2 E 2 4AF	.

		4A2
2A

Пример 6. Найти координаты и радиус окружности х2 у2 16у 9 0 .

3.2. Уравнение эллипса

Пусть в уравнении (17) В=0, но А С. Тогда (17) можно переписать в виде:

А(х-хо)2 + С(у-уо)2 = ,

(19)

где

; yo

;

4A2

4C2 F;

Если при этом А и С имеет одинаковые знаки, то уравнение (19) есть уравнение кривой, которая называется эллипсом (кривой эллиптического типа) с центром в точке с координатами

(хо, уо).

Если центр эллипса находится в начале координат, то

Если А 0, C 0, 0.

Ах2 + Су2 =

(20)

Получается каноническое уравнение эллипса

(21)

с полуосями a

х2 + у2 = а2.

При a = b - это уравнение окружности

(Если < 0, то кривая не имеет действительных точек; если =0, то кривая представляет собой одну точку (0;0)).

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

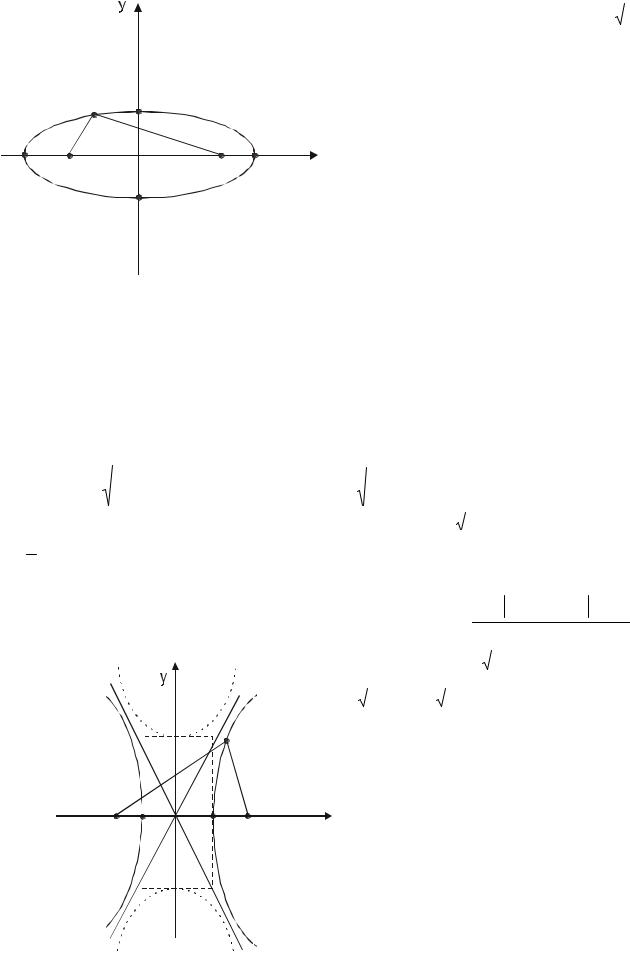
Точки F1 (-c; 0) и F2 (c; 0), где c

b2 ,

называются фокусами эллипса,

а отношение

- его эксцентриситетом.

M(x,y)

В1

Он характеризует форму эллипса. Очевидно,

А1

А2

что 0 1, причем для окружности ε=0.

Точки

А1(-а;0),

А2(а;0), В1(0;b),

В2(0;-b)

называются вершинами эллипса.

В2

Характеристическое свойство эллипса: для

любой точки эллипса сумма расстояний от

этой точки М(х,у) до фокусов F1

и F2

постоянна и равна 2а. (МF1 + MF2 = 2a)

Пример 7. Определить вид и расположение кривой

х2 + 2у2 – 4х + 16у = 0.

3.3. Гипербола

Кривая второго порядка (20) называется гиперболой (кривой гиперболического типа),

если коэффициенты А и С имеют разные знаки, т.е. АС 0.

Пусть для определённости А > 0, С <0.

Возможны случаи: А) δ > 0; Б) δ = 0;

В) δ ˂ 0.

А) В случае 0: каноническое уравнение гиперболы имеет вид:

(22)

где a

- действительная полуось, b

- мнимая полуось.

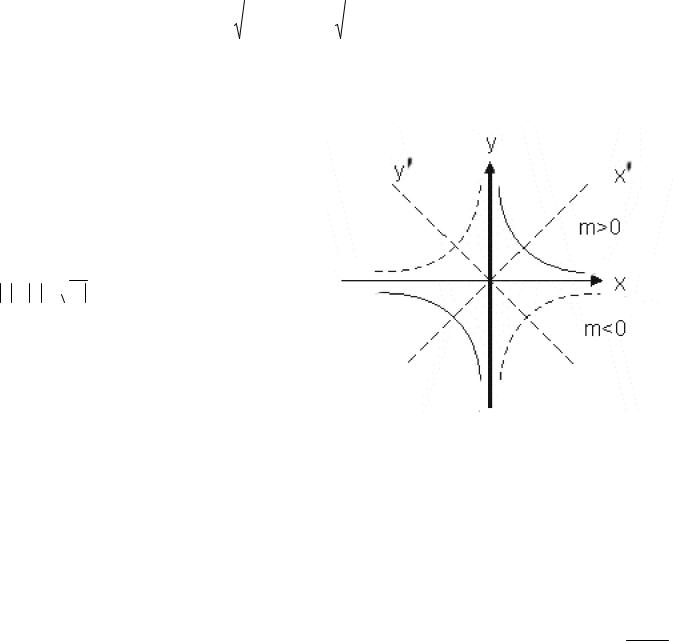
Фокусы гиперболы – точки F1 (-c; 0) и F2

(c; 0), где c

, а ее эксцентриситет

c принимает любые значения, большие 1. Вершины гиперболы точки – А1 (а; 0) и А2 (-а; 0). a

Характеристическое свойство гиперболы: для любой точки гиперболы абсолютная

величина разности ее расстояний до фокусов постоянна и равна 2а: d F2 M MF1 2a

Это часто принимается за определение гиперболы.

	M(x,y)
А2	А1
F2	F1

(22)

a 2

При

больших х

Т.е.

при х ,

ветви

x2 a 2

x2 x .

гиперболы как угодно близко подходят к

прямым

(23)

–

асимптотам

гиперболы.

(a=b)

Для

равносторонней

гиперболы

X х2 у2 а 2

асимптоты

х взаимно

являются биссектрисами

перпендикулярны

координатных углов.

Б) При δ = 0 уравнение Ах2 + Су2 = 0.

y 2

т.е.

получили

пару

пересекающихся

прямых

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

0 .

В) При 0 каноническое уравнение гиперболы имеет вид:

(24)

Она имеет полуоси a

и называется сопряженной гиперболой

(изображена на рисунке пунктиром).

Рассмотрим обратную пропорциональную зависимость:

y	m	(25)
	x

Её графиком является

равносторонняя гипербола, в которой

асимптотами являются оси координат. При m 0 ветви гиперболы

расположены в I и III квадрантах,

при m 0 – во II и IV квадрантах. Координаты любой вершины гиперболы равны по абсолютной величине, т.е.

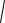
х у т , а их знаки определяются в

зависимости от квадранта, в котором расположена каждая вершина.

График дробно-линейной функции

y	ax в	,	(26)

	сх d

где с 0, bс–ad 0,

также представляет собой равностороннюю гиперболу, полученную параллельным

переносом

осей

координат с новым

центром в точке

. Асимптотами такой

;

)

O (

гиперболы являются прямые x

; у

с.

Пример 8.

Написать уравнение гиперболы с асимптотами

х и проходящей через

точку

. Найти расстояние между её вершинами.

Пример 9. Найти координаты центра, вершин и уравнения асимптот гиперболы у 3 2х .

х 1

3.4. Парабола

Пусть в уравнении (17) В=0, а также один из коэффициентов А или С равны нулю. Пусть

А=0, С 0, тогда

Су2 + Dx + Ey + F = 0

(27)

При D=0 (27) дает две прямые у=у1

и у=у2, где у1, у2 –корни квадратного уравнения

Су2+Еу+F=0.

При D 0, дополнив члены, содержащие у, до полного квадрата, получим уравнение кривой,

которая называется параболой:

у у0 2

2 р х х0

(28)

где x

; у

;2р

4DC2

2С

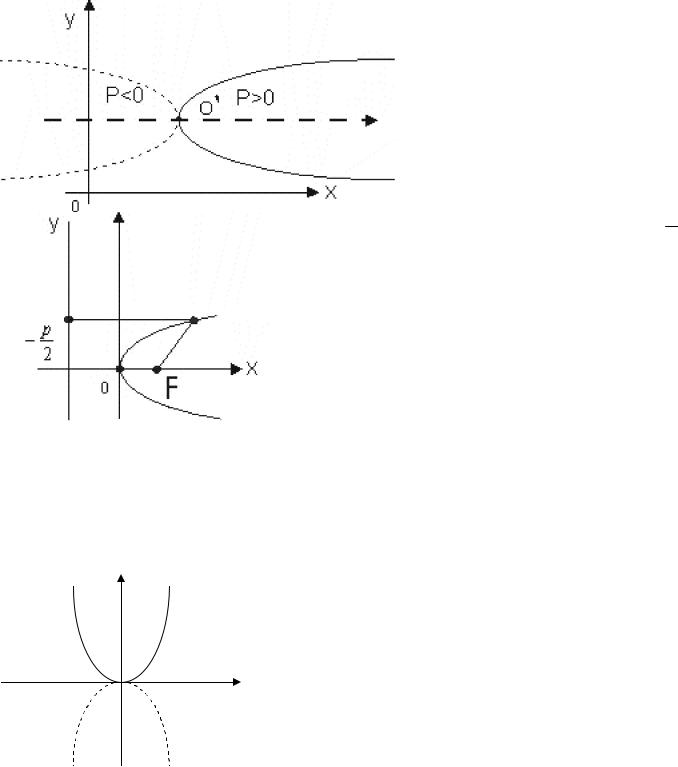
Точка О (хо, уо) называется вершиной параболы, число р – параметром параболы.

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

При р 0 ветви параболы направлены вправо, при р 0 – влево. Прямая у = уо является осью симметрии параболы. Если вершина параболы находится в начале координат, то уравнение (28) принимает вид:

у2 = 2рх

(29)

p
Точка F		;0	называется
	2

фокусом параболы, а прямая x p

- ее директрисой.

Парабола представляет множество всех точек плоскости, равностоящих от данной точки (фокуса) и от данной прямой (директрисы).

Если в уравнении (29)

поменять местами х и у, то получим:

х2=2ру

–уравнение параболы с вершиной в начале координат, симметричной относительно оси ординат.

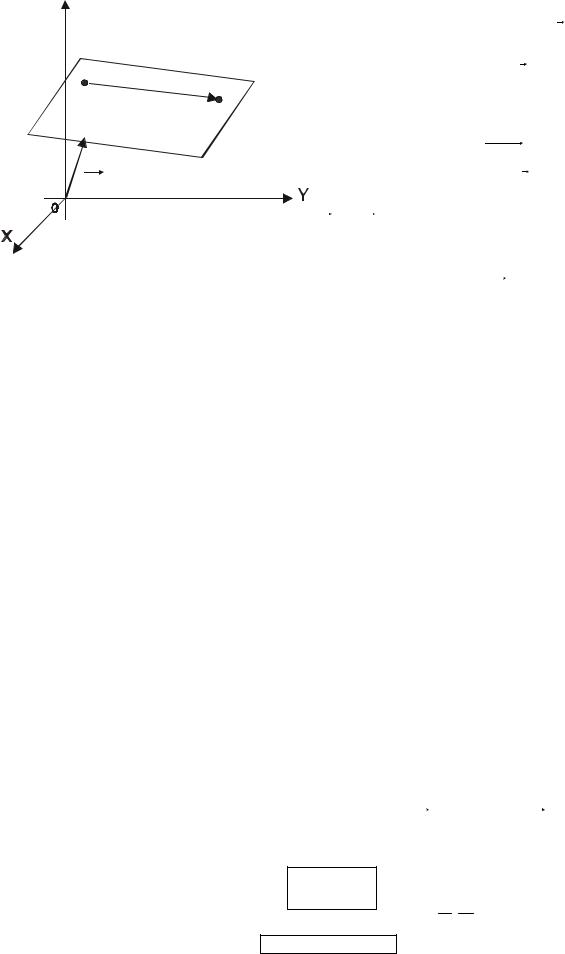
Его обычно записывают в виде

у=Ах2,

где А=

При А 0 ветви параболы направлены вверх, при А 0 – вниз.

2 p.

трехчлен у=Ах2 +

Квадратный

Вх

С (А 0)

преобразуется

в уравнение

параболы:

у =Ах 2

в системе

А>0

координат

x x

, y y

4AC B2

центром

4АС В2

;

. Эта парабола имеет вершину в точке

4А

с осью симметрии x

, параллельной оси Оу.

A<0

Пример 10. Построить кривую у 3х2 10х 3.


		Generated by Foxit PDF Creator © Foxit Software
		http://www.foxitsoftware.com					For evaluation only.
	Тема 2. Уравнения плоскости и прямой в пространстве
Z	В.1. Общее уравнение плоскости
			Пусть плоскость Q проходит через точку Мo(хo,
		уo, zo) перпендикулярно вектору n = (A,								B, C). Этими
		уo, zo) перпендикулярно вектору n = (A,								B, C). Этими
Мo		условиями определяется					единственная			плоскость	в
Мo	М	пространстве Охуz. Вектор					n называется нормальным
	М	вектором плоскости Q.
		вектором плоскости Q.
			Возьмем на плоскости Q произвольную точку М
	Q	(x, y, z).
	Q		Тогда		вектор	M 0 M =(х-хo, у-уo,				z-zo) будет
			Тогда		вектор	M 0 M =(х-хo, у-уo,				z-zo) будет
n		перпендикулярен вектору					n =(А,	В, С). Скалярное
		произведение			этих	векторов		равно		нулю,	т.е.
		n, M 0 M =0. Это уравнение в координатной форме имеет
		вид:		А (х-хo) + В (у-уo) + С (z-zo) = 0					(1)
Это уравнение плоскости, перпендикулярной данному вектору n (A, B,C) и проходящей
через данную точку Мo (хo, уo, zo).		Ах + Ву + Сz + D = 0				(2)
Уравнение плоскости в виде:		Ах + Ву + Сz + D = 0				(2)

(где D= – Ax0 – By0 – Cz0) называется общим уравнением плоскости.

Всякое уравнение 1-й степени с тремя переменными есть уравнение плоскости.

В.2. Неполные уравнения плоскости

Общее уравнение плоскости (2) называется полным, если все его коэффициенты А, В, С,

D≠0.

Если же хотя бы один из коэффициентов равен 0, то уравнение называется неполным. Виды неполных уравнений:

1.Если D=0, то Ах + Ву + Сz = 0 – плоскость проходит через начало координат.

2.если А = 0, то плоскость Ву + Сz + D = 0 параллельна оси Ох;

3.если В = 0, то Ах + Сz + D = 0 – параллельна оси Оу;

4.если С = 0, то Ах + Ву + D = 0 – параллельна оси Оz;

5.если А=D=0, то плоскость Ву + Сz = 0 проходит через ось Ох;

6.если В=D=0, то плоскость Ах + Сz = 0 проходит через ось Оу;

7.если С=D=0, то плоскость Ах +Ву = 0 проходит через ось Оz;

8.если А=В=0, то плоскость Сz + D = 0 параллельна плоскости Оху; в частности, если и D=0, то плоскость Сz=0 (или z=0) есть плоскость Оху;

9.если А=С=0, то плоскость Ву + D = 0 параллельна плоскости Охz; в частности, если D=0, то плоскость Ву = 0 (или y=0) есть плоскость Охz;

10.если B=С=0, то плоскость Ах + D = 0 параллельна плоскости Оyz; в частности, если D=0, то плоскость Ах = 0 (или x=0) есть плоскость Оyz.

В.3. Взаимное расположение двух плоскостей в пространстве

Рассмотрим

пространстве

две

плоскости:

A1 x B1 y C1 z D1

A2 x B2 y C2 z D2 0 .

Условия параллельности и перпендикулярности плоскости определяются условиями

коллинеарности и ортогональности их нормальных векторов n1 =(А1, В1, С1) и n2 =(А2, В2, С2). Условие параллельности – пропорциональность коэффициентов при одноименных

переменных (т.к. координаты нормальных векторов д.б. пропорциональны):

A1	B1	C1	(3)
A2	B2	C2

Условие перпендикулярности (скалярное произведение n1 ; n2 = 0):

А1А2+В1В2+С1С2=0 (4)

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Угол между плоскостями можно найти как угол между их нормальными векторами:

cos		A1 A2 B1 B2		C1C2			(5)

	A2	B2	C 2	A2	B2	C 2

1		1	1	2	2	2

В.4. Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой

Уравнение плоскости, проходящей через точки М1 (x1 , y1 , z1 ) , М 2 (x2 , y2 , z2 ) и М 3 (x3 , y3 , z3 ) , не принадлежащие одной прямой:

x x1

y y1

z z1

0 (6)

z3 z1

В. 5. Расстояние от точки до плоскости

Расстояние от точки М 0 (x0 , y0 , z0 ) до плоскости Ax By Cz D 0 :

Ax0

By0 Cz0

(7)

A2 B2

C 2

В. 6. Уравнение прямой в пространстве

Прямая в пространстве может быть задана как линия пересечения двух плоскостей, т.е. как множество точек, удовлетворяющих систему уравнений:

A x B y C z D 0,					(8)
1	1	1	1
A2 x B2 y C2 z D2 0.
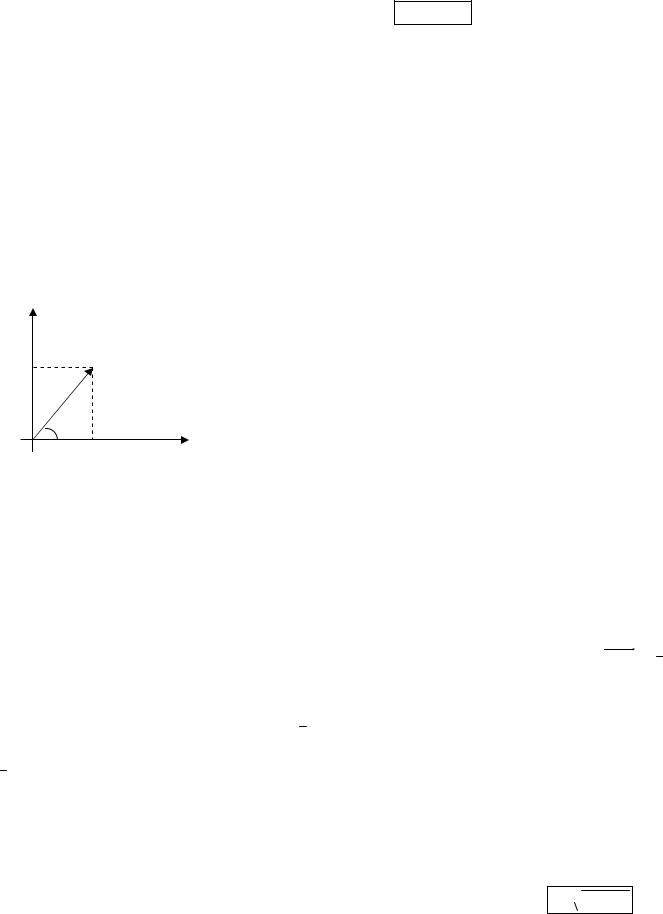
Если прямая проходит через точку М 0 (x0 , y0 , z0 ) ,				параллельно направляющему вектору

s =(l; m; n), то ее уравнение может быть получено из условия коллиниарности векторов M 0 M =(х-

хo, у-уo, z-zo) и s = (l; m; n):

x x0

y y0

(9)

(9) называется каноническим уравнением прямой в пространстве.

Параметрическое уравнение прямой в пространстве:

x l t x0

(10)

y m t y0

z n t z0

Уравнение

прямой,

проходящей

через

две

различные

точки

М1 (x1 , y1 , z1 ) ,

М 2 (x2 , y2 , z2 ) :

x x1

y y1

z z1

(11)

x2 x1

z2 z1

y2 y1

В.7. Взаимное

расположение прямой и

плоскости в пространстве

Прямая

x x0

y y0

z z0

и плоскость Ax By Cz D 0

- параллельны (или прямая лежит на плоскости):

Al Bm Cn 0

(12)

- перпендикулярны:

(13).

m n

М (х, у, z)

S=(m;n;p)

М (х1, у1, z1)

z x yi

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

Тема 3. Комплексные числа В.1. Основные понятия

Для решения многих задач физики, электротехники и др.наук возникла потребность

расширения понятия числа. Например, уравнение х2 1 0 не имеет решения в действительных числах.

Комплексными числами называются числа вида z x yi , где х и у – действительные

числа, а число i , определяемое равенством i2	1, называется мнимой единицей.
Действительное число х называется	действительной частью комплексного числа
( x R(z)), у - мнимой частью ( y I (z) ).

Выше приведённая запись комплексного числа называется алгебраической формой записи. Любое действительное число х содержится в множестве комплексных чисел: х x 0 i . Т.о.

множество действительных чисел является подмножеством множества комплексных. Множество комплексных чисел обозначается C (т.е. можно записать R C ).

Два комплексных числа z1 x1 y1i и z2 x2 y2i равны ( z1 z2 ) x1 x2 , y1 y2 . Число 0 можно записать: 0 0 0 i .

При х =0 комплексное число обращается в чисто мнимое y i .

Геометрическая интерпретация комплексного числа.

Комплексное число z x yi можно изобразить точкой на плоскости с координатами

(x, y) .

у M (x; y)

		х
О	х	х
	Плоскость	xOy , на которой изображаются комплексные числа, называется комплексной

плоскостью. При этом действительные числа изображаются точками оси абсцисс, которую называют действительной осью, а чисто мнимые числа – точками оси ординат, которую называют

мнимой осью.

Между множеством комплексных чисел и множеством точек плоскости xOy существует

взаимно-однозначное соответствие: каждому комплексному числу соответствует

единственная точка плоскости (x, y) , и наоборот, каждой точке соответствует единственное комплексное число.

Комплексное число z x yi можно геометрически изобразить в виде вектора OM z с

началом в точке О(0,0) и концом		в точке М (x, y) . Каждой точке М (x, y)			(каждому
комплексному числу z x yi ) будет соответствовать один и только один вектор.
	Два комплексных числа z x yi	и	z	x yi называют взаимно сопряжёнными, если их
действительные части равны, а мнимые имеют противоположные знаки. (Например,					z 2 3i и
z	2 3i .)

При решении квадратного уравнения z2 2z 2 0 получаем два взаимно сопряжённых корня: z1 1 i и z2 1 i .

Сопряжённые числа расположены симметрично относительно действительной оси. Комплексные числа z x yi и z x yi называются противоположными.

Противоположные числа симметричны относительно начала координат.

Модулем комплексного числа z x yi называется действительное число r x2 y2 .

arg(z) .

http://www.foxitsoftware.com For evaluation only.

В геометрической

интерпретации модуль –

это длина вектора

OM :

x2 y2 .

r 0 .

Модуль комплексного числа также называется абсолютной величиной этого числа.

Причём модуль

действительного числа

есть абсолютная

величина этого

числа:

x 0 i

x2 02

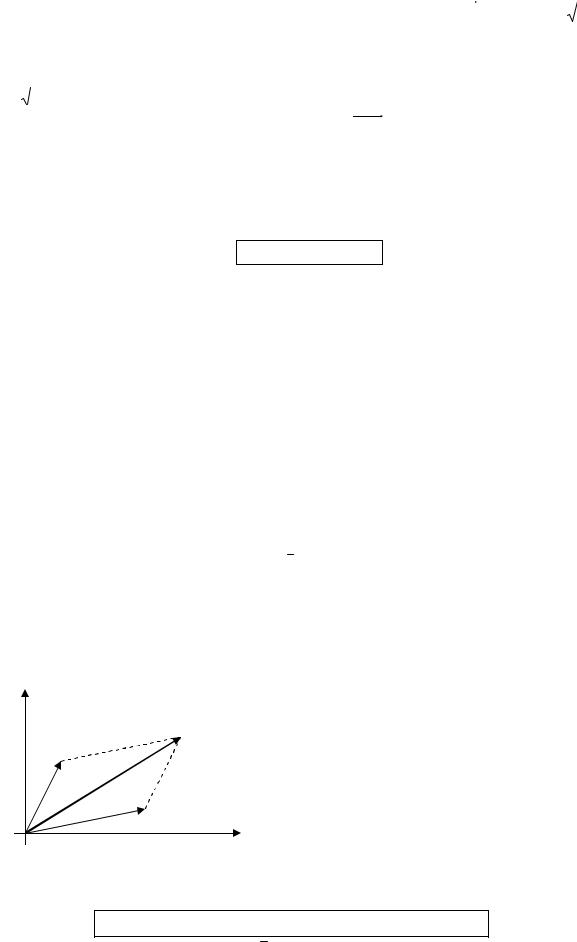
Угол между действительной осью Ох и вектором OM , отсчитываемый от положительного направления оси Ох, называется аргументом комплексного числа. Он определяется из соотношения:

	y	y	n ,n Z . Для числа z 0 аргумент не определен.
tg		arctg
	x
		x

Используя приведённые выше понятия, комплексное число можно записать в тригонометрической форме:

z r(cos isin ) .

Аргумент определён неоднозначно: вместо можно использовать n,n Z . Всю бесконечную совокупность значений аргумента комплексного числа z обозначают Arg(z).

Однако называется главным значением аргумента и обозначается

В.2. Действия с комплексными числами

Действия с комплексными числами удовлетворяют основным законам действий над рациональными числами. Между комплексными числами не существует понятий «больше» или «меньше».

Представление комплексного числа в алгебраической форме и рассмотрение мнимой единицы в качестве множителя, квадрат которого равен 1, позволяет производить операции с комплексными числами так же, как и с алгебраическими многочленами.

1. Сложение и вычитание комплексных чисел

Сложение двух комплексных

чисел z1 x1 y1i

z2 x2 y2i , записанных в

алгебраической форме, выполняется по формуле:

z1 z2 x1 y1i (x2 y2i) (x1 x2 ) (y1 y2 )i

Сумма двух сопряжённых чисел равна z

(x x) (y y)i 2x .

Пример 1. Найти сумму чисел z1

3 4i , и z2 5 3i .

Решение.

z z1 z2 (3 5) (4 3)i 2 7i .

Число z1

z2 геометрически изображается вектором,

построенным по правилу сложения

векторов (правило параллелограмма), соответствующих точкам z1

и z2 .

z1 z2

Вычитание двух комплексных чисел определяется как действие, обратное сложению. Разность двух комплексных чисел находится по формуле:

z1 z2 x1 y1i (x2 y2i) (x1 x2 ) ( y1 y2 )i .

Разность двух сопряжённых чисел z z (x x) (y y)i 2yi .

Пример 2. Найти разность z1 3 4i и z2 5 3i .

Решение. z z1 z2 (3 5) (4 3)i 8 i .

http://www.foxitsoftware.com For evaluation only.

2. Умножение комплексных чисел

Умножение двух комплексных чисел z1 x1 y1i и z2 x2 y2i выполняется по формуле:

z1 z2 x1 y1i (x2 y2i) (x1 x2 у1 у2 ) (х1 y2 х2 y1 )i

Правило умножения распространяется и на большее число сомножителей.

Пример 3. Найти произведение комплексных чисел z1 3 4i

и z2 5 3i .

Решение.

z1 z2

(3 4i)( 5 3i) 3( 5) 3 3i 4i( 5) 4i 3i 15 9i 20i 12i2

15 12 9i 20i 27 11i

При

умножении двух

комплексных

чисел,

записанных

тригонометрической

форме,

r1 (cos 1 isin 1 )

z2 r2 (cos 2

isin 2 ) ,

их

модули

умножаются, а аргументы

складываются:

z1 z2

r1r2 (cos( 1 2 ) isin( 1 2 ))

yi , получим

При умножении двух

сопряжённых чисел z x yi и

(x yi)(x yi) x2 y2 i2 x2

r2 , где r - модуль каждого из сомножителей.

Т.о. произведение двух сопряжённых комплексных чисел является действительным числом,

равным квадрату их модуля.

3. Деление комплексных чисел

Деление комплексных чисел рассматривается как действие, обратное к умножению:

x1 y1i

x1 x2 y1 y2

x2 y1 x1 y2

x2 y2i

x22 y22

Пример 4. Найти частное от деления числа z1

3 4i

на число z2 2 3i .

Решение. Умножим числитель и знаменатель на число, сопряжённое к знаменателю:

3 4i

(3 4i)(2 3i)

6 9i 8i 12i2

6 17i

i .

2 3i

(2 3i)(2 3i)

4 9i2

4 9

При

делении

двух

комплексных

чисел,

записанных

тригонометрической

форме,

r1 (cos 1 isin 1 ) и z2

r2 (cos 2 isin 2 ) , их модули делятся, а аргументы вычитаются:

(cos( 1 2 ) isin( 1

2 ))

4. Возведение комплексных

чисел в степень

Возведение комплексного числа z x yi

в степень n (n N) можно рассматривать как

частный случай умножения:

zn z z ... z .

раз

Для чисел, записанных в тригонометрической форме:

zn rn (cos(n ) isin(n ))

Пример 5. Вычислить z4						(1 i)4 .
Решение.
1 способ. z (1 i)4 (1 i)2 (1 i)2										(1 2i i2 )(1 2i i2 ) 2i 2i 4i2 4.
2 способ. Запишем комплексное число в тригонометрической форме:
						1
2	2


r 1	1		2 , arctg						z			2 cos		isin		.

													4
						1		4					4		4
Тогда z (				4							4( 1) 4 .
				4
		2)			cos4		isin 4
		2)			cos4	4	isin 4
						4				4

Корень степени n из комплексного числа z r(cos isin ) , не равного нулю, имеет точно n

значений:

n		n		arg z 2 k		arg z 2 k			.

	z		r cos		isin		,	k 0,1,...,n 1
				n		n

Пример 6. Вычислить 1 .

Решение. Полагаем z 1 0i . В тригонометрической форме: z 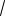1 cos isin .

1			1			2 k			2 k
1			1

(z)2	(	1)2		cos					i sin		,	k 0,1.
(z)2	(	1)2		cos					i sin	2	,	k 0,1.
						2				2
					1								1		3		3
При k 0: (z)2										i .	При k 1: (z)2				3	i sin	3	i .
						cos			isin					cos
						cos	2		isin					cos	2
							2	2							2	2

Раздел 3. Математический анализ и дифференциальные уравнения Тема 1. МНОЖЕСТВА И ФУНКЦИИ

В.1. Понятие множества

Множество – совокупность (собрание, набор) некоторых объектов.

Объекты, образующие множества, называются элементами (точками) данного множества.

Множества обозначаются прописными буквами латинского алфавита: А, В, С…, а элементы – строчными а, b, c… Принадлежность элемента а множеству А записывается следующим образом: а А . Запись b A означает, что элемент b не принадлежит множеству А.

Множество, не содержащее ни одного элемента, называется пустым и обозначается Ø. (например, множество действительных корней уравнения х2+4=0 – пустое множество).

Если множество В состоит из части элементов множества А или совпадает с ним, то В называется подмножеством множества А (обозначается В А ).

Равные множества состоят из одних и тех же элементов. Объединением множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы

одному из данных множеств ( А В).

А В

Пересечением множеств А и В называется множество, состоящее из элементов, одновременно принадлежащих

каждому из данных множеств ( А В ).

А В

Разностью множеств А и В называется множество, состоящее из всех элементов А, которые не принадлежат В

(А \ B).

А \ B

Дополнением множества А, являющегося подмножеством В ( А В ), называется множество АС, состоящее из всех элементов В, которые не принадлежат А.

			АС
Пример 1. а) Пусть даны два множества: А = {1, 2, 3, 4} и В = {2, 4, 5, 6}. Тогда их
объединением будет множество А В = {1, 2, 3, 4, 5, 6}; пересечением –			А В = {2, 4};
разностью А \ B = {1, 3}, В \ А = {5, 6}.
б) Даны множества А = {1, 2, 3} и В = {1, 2, 3, 4, 5, 6}. Очевидно, что А является
подмножеством В ( А В ). Тогда:
А В = {1, 2, 3, 4, 5, 6} = В;	А В = {1, 2, 3} = А;	В \ А = {4, 5, 6};	АС = {4, 5, 6}.

Множества, элементами которых являются действительные числа, называются числовыми. Например, числовыми являются множество натуральных чисел N, множество целых чисел Z, множество рациональных чисел Q, иррациональных I и множество

действительных чисел R, которые	связаны между собой следующим образом:
N Z Q R , I R , R = Q I.

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
26.03.201639.24 Кб17Маркетинг.Кашапов Р.С.гр-541ДЗ.docx
#
20.11.20193.41 Mб180Марченко.Мачин.ИППУ.doc
#
01.06.2015340.13 Кб18мат. стат.pdf
#
01.06.2015134.33 Кб6матан индивидуалка.pdf
#
12.09.2019160.49 Кб6матан с 41 по 43.docx
#
01.06.2015927.18 Кб7Матем_лекции_ 1сем_гр.,2621,2721.pdf
#
10.11.20191.26 Mб10Математика и статистика_1сем (рекл).doc
#
04.11.20181.24 Mб12Математика лекции 1сем-р.doc
#
27.11.20191.17 Mб14Математика от Заплавной Т.А..doc
#
17.11.20192.74 Mб5Математика ТМ.doc
#
01.06.2015386.21 Кб8Математика_КР_ОЗО_1сем_2012_гр2621,2721.pdf