
Матем_лекции_ 1сем_гр.,2621,2721
.pdf
|
|
|
|
|
|
|
|
|
Generated by Foxit PDF Creator © Foxit Software |
|||||||
|
|
x |
a |
|
x 1 |
a |
|
http://www.foxitsoftware.com For evaluation only. |
||||||||
|
|
11 |
21 |
x |
2 |
... a |
n1 |
x n , |
|
|||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x2 |
a12 x 1 |
a22 x |
2 |
... an2 x n , |
|
|||||||||
|
............................................... |
|
|
|||||||||||||
|
|
xn |
a1n x 1 |
a2n x |
2 |
.... ann x n |
|
|||||||||
или в матричной форме: |
|
X A' |
X , |
|
|
|
|
|
|
|
|
|
||||
|
X (A 1 ) X |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||||||
|
|
В.5. Евклидово пространство |
|
|||||||||||||
|
Скалярным произведением двух векторов x (x1 ,..., xn ) |
и y (y1 ,..., yn ) называется |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
число: |
|
(x, y) x1 y1 x2 y2 ... xn yn |
xi yi |
|
|
|
|
|||||||||
|
Экономический |
|
|
|
|
|
|
|
|
|
i 1 |
: если x (x1 ,..., xn ) вектор объемов |
||||
|
смысл скалярного произведения |
|||||||||||||||
различных товаров, а y (y1 ,..., yn ) - |
вектор их цен, то ( x, y )- |
суммарная стоимость этих |
||||||||||||||
товаров. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Свойства скалярного произведения:
1.(x, y) ( y, x) коммутативность;
2.(x, y z) (x, y) (x, z) дистрибутивность;
3.( x; y) (x, y), однородность;
4.(x, x) 0, если x 0, (x, x) 0, если x 0.
Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным четырем свойствам ( рассматриваемым как
аксиомы), называется евклидовым пространством. |
|
|
|
|
|
|
|||||||
Длиной (нормой) вектора x в евклидовом |
|
пространстве называется корень |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
квадратный из его скалярного квадрата: |
|
x |
|
|
|
= x |
2 |
x |
|
2 ... x |
2 |
|
|
|
|
(x, x) |
2 |
||||||||||
|
|
|
|
1 |
|
|
n |
||||||
Свойства длины вектора:
1.x 0 x 0;
2.x x , действительное число;
3.(x, y) x y (неравенство Коши-Буняковского);
4.x y x y -( неравенство треугольника).
Угол между двумя векторами x и y определяется равенством:
cos |
|
|
(x, y) |
, где 0 . |
||||
|
|
x |
|
|
|
y |
||
|
|
|
|
|||||
|
|
|
|
|
|
|||
Два вектора называются ортогональными, если их скалярное произведение равно нулю. Очевидно, что нулевой вектор ортогонален любому другому вектору. Если два
ненулевых вектора ортогональны, то / 2. |
|
|
|
||
Векторы |
e1 , e2 ....,en |
n-мерного |
евклидова |
пространства |
образуют |
ортонормированный базис, если (ei , e j ) 0, i j, ei 1,i 1, n.
Теорема. Во всяком n-мерном евклидовом пространстве существует ортонормированный базис.
Пример: система n единичных векторов ei , у которых i -ая компонента равна единице, а остальные –нулю: e1 (1,0,...,0)' , e2 (0,1,0,...,0)' ,....,en (0,...,0,1)' .
В.6. Линейные операторы
Рассмотрим два линейных пространства: R n размерности n и Rm размерности m.
21

|
|
Generated by Foxit PDF Creator © Foxit Software |
|||||
|
|
http://www.foxitsoftware.com For evaluation only. |
|||||
Если задан закон (правило), по которому |
каждому |
вектору |
x Rn |
ставится в |
|||
соответствие единственный |
вектор y Rm , то |
говорят, |
что |
задан |
оператор |
||
(преобразование, отображение) А(х), действующий из R n в Rm , и записывают у=А( х). |
|||||||
Оператор |
называется |
линейным, |
если |
для |
любых |
векторов |
|
a, b Rn , выполняются соотношения:
~~ ~
1.A(a b) A(a) A(b) свойство аддитивности;
~~
2.A( a) A(a) свойство однородности оператора.
Вектор |
~ |
называется образом вектора х, а сам вектор х- прообразом вектора |
||||||||||||
y A(x) |
||||||||||||||
y. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если пространства R n |
|
и Rm совпадают, то оператор А отображает пространство R n |
||||||||||||
в себя. Рассмотрим именно этот случай. |
|
|
|
|
|
|||||||||
Выберем в R n |
базис |
e , e |
2 |
,...,e |
n |
, запишем разложение произвольного вектора x по |
||||||||
этому базису: |
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x1e1 |
x2 e2 ... xn en . |
|
|
|
|
|
|
~ |
|
|
||||
Применим к этому выражению линейный |
|
оператор |
силу его |
линейности |
||||||||||
|
A, в |
|||||||||||||
получаем: |
~ |
~ |
|
|
|
|
~ |
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
||||
A(x) x1 A(e1 ) x2 A(e2 ) |
... xn A(en ). |
|
|
|
|
|
||||||||
|
~ |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
),i 1, n -также |
вектор из R |
, то его можно |
разложить |
по базису |
|||||||||
Поскольку A(ei |
|
|||||||||||||
e1 , e2 ,...,en :
~
A(ei ) a1i e1 a2i e2 ... ani en , (i 1, n)
Тогда
~ |
(a11e1 |
|
an1en ) x2 (a12 e1 |
an2 en ) |
xn (a1n e1 |
ann en ) |
A(x) x1 |
Перегруппируем сомножители в правой части, вынося за скобки базисные векторы, e1 , e2 ,...,e3 , получим:
~ |
a12 x2 |
... a1n xn )e1 (a21 x1 a22 x2 ... a2n xn )e2 ...(an1 x1 an2 x2 ... ann xn )en |
(*) |
||
A(x) (a11 x1 |
|||||
С другой стороны, вектор |
~ |
имеющий в том же базисе e1 , e2 ,...,en координаты |
|||
y A(x), |
|||||
y1 , y2 ,..., yn можно записать так:
~
A(x) y1e1 y2 e2 ... yn en . (**)
Разложение вектора по базису единственно, следовательно, правые части (*) и (**) равны, поэтому:
|
|
y1 |
a11 x1 |
a12 x2 |
... a1n xn , |
|
|
|
|||||||||
|
|
|
|
a21 x1 |
a22 x2 |
... a2n xn |
, |
|
|||||||||
|
|
y2 |
или в матричной форме: Y AX. |
||||||||||||||
|
|
............................................. |
, |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
n |
a |
n1 |
x |
a |
n2 |
x |
2 |
... a |
nn |
x |
|
n |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||
|
|
Матрица |
A (aij ),(i, j |
|
каждый столбец которой состоит из координат образа |
||||||||||||
~ |
|
1, n), |
|||||||||||||||
) |
соответствующего базисного |
вектора ei в том же базисе e1 , e2 ,...,en , называется |
|||||||||||||||
A(ei |
|||||||||||||||||
матрицей оператора |
|
~ |
|
|
|
|
~ |
||||||||||
|
A в базисе |
e1 , e2 ,...,en , а ранг r матрицы А рангом оператора A . |
|||||||||||||||
Таким образом, каждому линейному оператору соответствует матрица в данном базисе. Наоборот, всякой матрице n-го порядка соответствует линейный оператор n- мерного пространства.
Вектор х и его образ |
~ |
связаны матричным уравнением: |
|
Y AX , |
|||||||
y A(x) |
|
||||||||||
где А- матрица линейного оператора X (x , x |
2 |
,..., x |
n |
),Y (y |
y |
2 |
,..., y |
n |
)' . |
||
|
|
1 |
|
1 |
|
|
|
||||
22

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Generated by Foxit PDF Creator © Foxit Software |
|
|||||||||||||||||
|
|
|
|
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
http://www.foxitsoftware.com |
For evaluation only. |
|
|||||||||||||||||||||
|
|
|
|
|
Линейный |
|
оператор |
|
в |
R |
3 |
в |
|
базисе |
e1 , e2 , e3 |
|
задан |
матрицей |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
A |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
3 |
2 |
|
4 |
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
x 4e1 |
3e2 |
e3 . |
|
|
|
|
|
|
|
|
|
|
|||||||||
A 1 |
|
6 Найти образ |
A(x) вектора |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
8 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
3 |
2 4 4 |
|
|
10 |
|
|
|
||||||||
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Применяем формулу перехода: y2 |
|
1 |
6 3 |
13 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
Образ вектора х имеет вид: |
|
|
|
|
|
|
y3 |
|
|
8 6 |
|
|
18 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
y 10e1 |
13e2 18e3 . |
~ |
|
|
~ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
Суммой |
двух |
линейных |
|
|
операторов |
|
|
и |
|
называется |
оператор |
|||||||||||||||||||||||||||
~ |
|
|
|
|
|
A |
|
B |
|
||||||||||||||||||||||||||||||||||
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(A B), определяемый равенством: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
~ |
|
|
~ |
|
~ |
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
(A |
B)(X ) A(X ) B(X ). |
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
Произведением |
линейного |
|
оператора |
на |
число |
|
называется |
оператор |
||||||||||||||||||||||||||||||
|
~ |
|
|
|
|
|
A |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( A)(X ) (A(X )). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
~ |
|
|
|
|
|
|
|
|
|
~ ~ |
|
|
|
||||||||||||||
|
|
|
|
|
Произведением линейных операторов |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
A и B называется оператор AB : |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
~ |
~ |
|
|
|
~ ~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
(AB)(X ) A(B(X )). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Все эти операторы удовлетворяют свойствам аддитивности и однородности, т.е. |
||||||||||||||||||||||||||||||||||||||
являются линейными. |
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
||||||||||||
|
|
|
|
|
Нулевой оператор |
переводит все векторы из R |
n |
в нулевые векторы |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
0(0) 0. |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
Тождественный оператор |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
E(X ) X. |
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
Теорема. |
Матрицы |
|
|
A и A |
|
линейного |
оператора |
|
в |
базисах e1 , e2 ,...,en и |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
A |
|
|||||||||||||||||||||||||||||||||
e |
, e |
2 |
,...,e |
|
связаны соотношением: |
|
A |
C 1 AC, |
|
где |
|
C матрица |
перехода от старого |
||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
базиса к новому. |
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
17 |
6 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
Пример. В базисе e , e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти матрицу оператора |
||||||||||||||||||||||
|
|
|
|
|
2 |
оператор A имеет матрицу A |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e1 2e2 ; |
|
2e1 |
e2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
A в базисе |
|
e 1 |
e |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
Решение. |
Матрица |
|
|
перехода |
|
здесь |
|
C |
1 |
|
2 |
|
|
|
,а |
обратная |
к |
ней |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|||
C |
1 |
|
|
1 1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
5 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Следовательно, |
A |
|
|
|
1 1 |
2 17 |
6 1 |
|
2 |
5 |
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 2 |
|
|
8 2 |
|
1 |
0 |
20 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
В.7. Собственные векторы и собственные значения линейного оператора |
~ |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
Вектор |
x 0 называется |
собственным вектором линейного |
оператора |
если |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
A, |
||||||||||||||||||||||||||||||||||||||
найдется такое число , что |
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(*) |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
A(x) x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|||||||||||||||||||
|
|
|
|
|
Число |
|
называется |
|
|
|
собственным |
значением |
оператора |
|
(матрица |
А), |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
A |
||||||||||||||||||||||||||||||||||
соответствующим вектору x. Под действием линейного оператора |
~ |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
A собственный вектор |
|||||||||||||||||||||||||||||||||||||||||||
переходит в вектор, коллинеарный самому себе. Перепишем (*) в матричной форме: Ax x
В развернутом виде:
23

Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
a11 x1 a12 x2 .... |
a1n xn x1 , |
|||||||||||
|
|
a22 x2 |
a2n xn x2 |
, |
||||||||
a21 x1 |
||||||||||||
............................................. |
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
x |
a |
n2 |
x |
2 |
..... |
a |
nn |
x |
n |
x |
n |
|
n1 1 |
|
|
|
|
|
|
|||||
Представим в однородном виде:
(a11 )x1 |
a12 x2 ... |
a1n xn 0 |
|||||||||
|
|
(a22 )x2 |
|
a2n xn 0, |
|||||||
a21 x1 |
|
||||||||||
.................................................. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
x |
a |
n2 |
x |
2 |
... |
(a |
nn |
)x |
n |
0. |
|
n1 1 |
|
|
|
|
|
|
||||
Эта система (однородная) всегда имеет нулевое (тривиальное) решение х=0. Для существования ненулевого решения необходимо и достаточно, чтобы определитель системы равнялся нулю:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a11 |
a12 |
|
|
a1n |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A E |
|
|
a21 |
a22 |
|
|
a2n |
|
= 0 |
|
(**) |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an1 |
an2 |
|
ann |
|
|
|
|
|
|
||||||||
|
|
|
Определитель |
|
|
|
A E |
|
|
является многочленом n-ой степени относительно . |
Это – |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
характеристический |
|
|
|
многочлен |
|
|
оператора |
~ |
или |
матрицы |
А, а уравнение |
(**) – |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
A |
||||||||||||||||||||||||||||||||||||||||||||||||||
характеристическое уравнение оператора |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
A или матрицы А. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Характеристический многочлен линейного оператора не зависит от выбора базиса, |
||||||||||||||||||||||||||||||||||||||||||||||||||||
т.е. |
|
A E |
|
|
|
A |
|
E |
|
, |
|
где |
A, A |
|
|
матрицы |
оператора |
~ |
|
в |
старом и |
новом базисах |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
A |
|
||||||||||||||||||||||||||||||||||||||||||||||
соответственно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Пример. |
|
Найти |
собственные |
значения |
и |
собственные |
векторы линейного |
оператора |
|||||||||||||||||||||||||||||||||||||||||||||||
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A, заданного матрицей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
А = |
|
9 |
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Решение. |
|
Составим характеристическое уравнение |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
A E |
|
|
|
1 |
|
|
4 |
|
|
0, или 2 2 35 0, |
откуда |
5; |
2 |
7. |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
9 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Находим собственный вектор x(1) , |
отвечающий собственному значению |
5: |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
(A E)x(1) |
|
|
|
0 |
|
|
или |
|
6 |
|
4 |
|
x (1) |
|
|
|
0 |
|
|
x |
|
|
(1) |
1,5cx(1)1 ; Примем |
x |
(1) |
c :отсюда |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
, откуда |
2 |
|
|
||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
x2 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
||||||||||
векторы x |
(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
(c, 1,5c); c 0 являются собственными векторами линейного оператора A с |
|||||||||||||||||||||||||||||||||||||||||||||||||||
собственным значением 5. |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
Аналогично |
|
|
для |
|
2 |
7 |
|
|
векторы |
x(2) ( |
c, c)' , c 0 |
являются |
собственными |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||
векторами линейного оператора |
|
с собственным значением 2 |
7. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
A |
~ |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Наиболее простой вид принимает матрица А линейного оператора |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
A , имеющего n |
||||||||||||||||||||||||||||||||||||||||||||||||||||
линейно независимых |
собственных |
векторов e1 , e2 ,...,en |
с |
|
собственными значениями , |
||||||||||||||||||||||||||||||||||||||||||||||||||
соответственно равными 1 , 2 ,..., n . |
Матрица оператора |
~ |
в базисе, составленном из его |
||||||||||||||||||||||||||||||||||||||||||||||||||||
A |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
собственных векторов, является диагональной и имеет вид:
24

|
Generated by Foxit PDF Creator © Foxit Software |
||||
|
http://www.foxitsoftware.com For evaluation only. |
||||
1 |
0 |
... |
0 |
|
|
0 |
2 |
... |
0 |
|
|
A |
... |
... |
|
|
|
... |
... |
|
|||
|
0 |
... |
|
|
|
0 |
n |
~ |
|||
Верно и обратное: если матрица А линейного оператора |
|||||
A в некотором базисе является |
|||||
~
диагональной , то все векторы этого базиса – собственные векторы оператора A.
Кроме того, если линейный оператор имеет n попарно различных собственных значений , то отвечающие им собственные векторы линейно независимы, и матрица этого оператора в соответствующем базисе имеет диагональный вид.
В.8. Линейная модель обмена(модель международной торговли
Пусть n стран S1 , S2 ,...,Sn имеют национальный доход x1 , x2 ,..., xn соответственно, aij доля национального дохода, которую j-ая страна тратит на покупку товаров у i-ой страны. Считаем, что весь национальный доход тратится на закупку товаров либо внутри
|
|
|
n |
|
|
|
страны, либо на импорт из других стран, т.е. aij |
1,( j |
1, n) |
(1) |
|||
|
|
|
i 1 |
|
|
|
a11 |
a12 |
... |
a1n |
|
|
|
|
|
|
|
|
|
|
Матрица A a21 |
a22 |
... |
a2n называется структурной матрицей торговли. |
|||
... ... |
.... |
... |
|
|
|
|
|
an2 |
... |
|
|
|
|
an1 |
ann |
|
|
|
||
В соответствии с выражением (1) сумма элементов любого столбца равна единице. Для i--ой страны выручка от внутренней и внешней торговли составит:
pi ai1 x1 ai2 x2 ... ain xn .
Для сбалансированной торговли необходима бездефицитность торговли каждой стран, т.е. выручка от торговли каждой страны должна быть не меньше ее национального
дохода: pi xi , (i 1, n).
Отсюда получаем систему неравенств:
a11 x1 a12 x2 |
... |
a1n xn x1 , |
|
|
|||||||||
|
|
a22 x2 |
a2n xn |
x2 |
, |
|
|||||||
a21 x1 |
(2) |
||||||||||||
.......................................... |
|
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
x |
a |
n2 |
x |
2 |
.... |
a |
nn |
x |
n |
x |
n |
|
|
n1 1 |
|
|
|
|
|
|
|
|||||
Сложим все неравенства, получим после группировки:
x1 (a11 a21 ... an1 ) x2 (a12 |
a22 |
... an2 ) ... xn (a1n |
a2n ... ann ) x1 x2 ... xn . |
|||||||||||||
Учитывая (1), имеем x1 |
x2 |
... xn x1 x2 |
... xn . |
|
|
|
|
|
||||||||
Неравенство pi xi |
невозможно, условие |
pi |
xi |
принимает |
вид |
pi |
xi (i |
|
|
|||||||
1, n). С |
||||||||||||||||
экономической точки |
зрения |
это |
означает, что |
все |
страны не |
могут |
одновременно |
|||||||||
получать прибыль. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Введем вектор х=( x , x |
2 |
,..., x |
n |
)' |
(векторстолбец), получим уравнение |
|
|
|
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
(3) |
|
|||
|
|
|
|
|
|
|
|
Ax x |
|
|
|
|
|
|
||
Задача сводится к отысканию собственного вектора матрицы А, отвечающего |
||||||||||||||||
собственному значению 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
1/ 3 1/ 4 |
1/ 2 |
||||
Пример. Структурная матрица торговли трех стран имеет вид: A 1/ 3 |
1/ 2 |
1/ 2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1/ 4 |
|
||
|
|
|
|
|
|
|
|
|
|
|
1/ 3 |
0 |
||||
Найти национальные доходы стран для сбалансированной торговли.
25

|
|
|
|
|
|
|
|
|
Generated by Foxit PDF Creator © Foxit Software |
||||||||
|
|
|
|
|
|
|
|
|
http://www.foxitsoftware.com For evaluation only. |
||||||||
Решение. Решим уравнение (A E)x 0 : |
|
|
|
|
|
|
|
||||||||||
2 / 3 |
1/ 4 1/ 2 x1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
1/ 3 |
1/ 2 |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
1/ 2 x2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
1/ 3 |
1/ 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x3 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
Методом Гаусса найдем решение: |
x |
|
3 |
c; x |
|
2c; x |
|
c; т.е. |
x ( |
3 |
c;2c; c)' . |
||||||
|
2 |
3 |
|
||||||||||||||
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: Для сбалансированной торговли соотношение национальных доходов должно
быть 3 : 2 :1или 3:4:2.
2
26

Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
Раздел 2. «Аналитическая геометрия» Тема 1. Уравнение линии на плоскости
Рассмотрим на плоскости некоторую линию у (кривую). Координаты х и у точки, лежащей на этой линии, должны быть связаны некоторым образом. Эта связь аналитически записывается
в виде некоторого уравнения.
М(х,у)
О х
Опр. Уравнением линии (кривой) на плоскости Oxy называется уравнение, которому удовлетворяют координаты x и у каждой точки данной линии и не удовлетворяют координаты
любой точки, не лежащей на это линии. |
F(x,y) = 0 |
В общем виде уравнение линии: |
|
или, если это возможно: |
у = f (x). |
Если т.М(х, у) передвигается по линии, то её координаты, изменяясь, удовлетворяют уравнению этой линии. Поэтому координаты т.М называются текущими.
Любую линию на плоскости можно выразить соответствующим уравнением, но не всякое
уравнение определяет на плоскости некоторую линию. Например, х2 у2 |
0 , |
х2 у 2 9 0 . |
|
|
|||||||||
Чтобы убедиться, лежит ли точка М на данной линии F(x,y) = 0, надо проверить, |
|||||||||||||
удовлетворяют ли её координаты уравнению этой линии. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
В.1. Уравнение прямой |
|
|
|
|
|
|
|
|
|
|
|
|
1.1. Уравнение прямой с угловым коэффициентом |
|
|
|
|
|
|
|
|
|||
Пусть прямая пересекает ось Оу в точке В 0; b ) и образует с осью Ох угол (0 |
). |
|
|
||||||||||
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|||
Возьмём |
на |
прямой |
произвольную |
точку М(х, |
у) |
tg |
MN |
|
y b |
. |
|||
|
|
||||||||||||
|
|
|
|
|
|
|
NB |
x |
|||||
M(x,y)
B(0;b) |
N(x,b) |
|
b
X
|
0 |
A(x,0) |
|
|
|
||||||
|
|
|
y b |
|
|||||||
Введем угловой коэффициент прямой k tg , т.е. k |
|
||||||||||
|
|||||||||||
|
|
|
|
|
|
|
|
(1) |
x |
||
|
|
|
|
|
|
y kx b |
|
|
|
||
(1) |
– уравнение прямой с угловым коэффициентом. |
||||||||||
Формула справедлива и для |
|
|
. |
|
|
|
|||||
2 |
|
|
|
||||||||
Частные случаи (1): |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
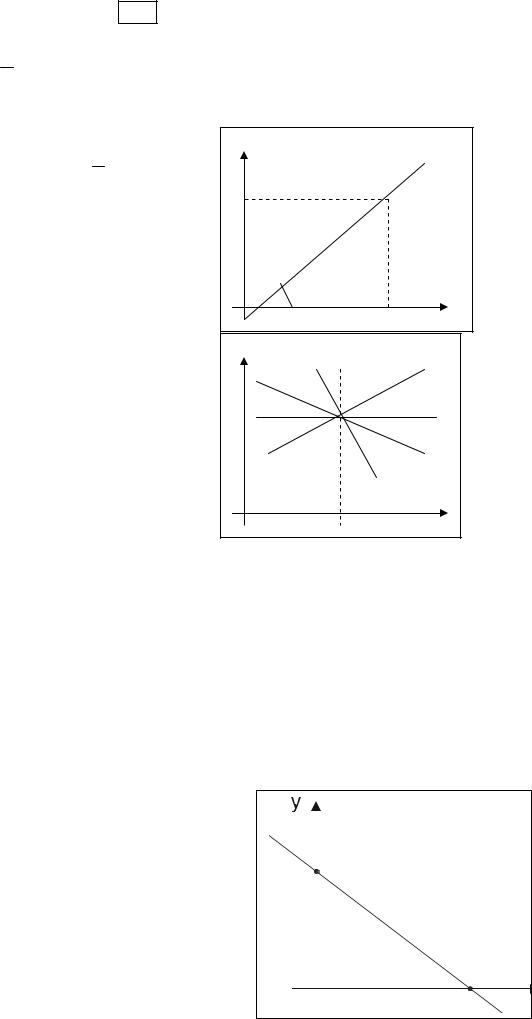
1. |
b = 0; у = kx – |
|
уравнение прямой, |
проходящей через начало координат и |
|||||||
образующей при k tg >0 – острый угол с Ох, k < 0 – тупой угол.
В частности биссектриса 1 и 3 координатных углов имеет вид у = х, а 2-го и 4-го у = -х;
27
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
2.= 0; k = tg 0 = 0; y b – уравнение прямой, параллельной оси Ох. В частности,
если b = 0, то у = 0 – ось Ох;
3.= -вертикальная прямая, у которой не существует углового коэффициента; х = а,
2
прямая пересекает ось Ох в точке х = а. В частности при а = 0 получаем ось Оу.
1.2. Уравнение прямой, проходящей через данную точку в данном направлении
Пусть прямая проходит через М1 |
(х1,у1) |
у |
|
|
и образует с осью Ох угол .
|
2 |
|
Т.к. т. М1 |
(х1,у1) принадлежит прямой, у1 |
М1 |
следовательно |
её координаты удовлетворяют |
|
уравнению (1): |
|
|
y1 kx1 b . Вычтем это равенство из (1) => |
|
|
у – у1 = k∙(x –x1) |
|
|
(2) |
α |
х |
||
|
|
|
|
|
|
||
Если в (2) k – произвольное число; задав |
|
х1 |
|||||
|
|
||||||
его, можно задать конкретную прямую. Это |
у |
|
|||||
уравнение |
называется |
также |
уравнением |
|
|
||
пучка прямых, проходящих через т. М1 (х1,у1), |
|
|
|||||
кроме прямой, параллельной оси Оу. |
|
М1 |
|||||
Пример |
1. |
Составить |
уравнения |
|
|
||
прямых, проходящих через точку А(3; -2): |
|
|
|||||
А) под углом 135о к оси Ох; |
|
|
|||||
Б) параллельно оси Ох; |
|
|
|
||||
В) параллельно оси Оу; |
|
|
х |
||||
Г) записать уравнение пучка прямых. |
|
|
|||||
1.3. Уравнение прямой, проходящей через 2 точки
Пусть прямая, проходит через точки М1 (х1,у1) и М2 (х2,у2), х1 х2 , у1 у2 . Запишем уравнение пучка прямых, проходящих через точку М1: у – у1 = k∙(x –x1).
Т.к. т. М2 принадлежит этой |
прямой |
=> |
у2 – у1 |
= k∙(x2 –x1). |
=> |
k |
y2 |
y1 |
||||||||
x2 |
x1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
=> y y |
y2 |
y1 |
x x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
x2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
=> |
|
y y1 |
|
|
x x1 |
|
|
(3) |
|
|
|
|
||
|
|
|
|
|
x2 x1 |
|
|
|
|
|||||||
|
|
|
|
|
y2 y1 |
|
|
|
|
|
|
|||||
Пример 2. Записать уравнение прямой, проходящей через точки А(-5;4), В(3;-2)
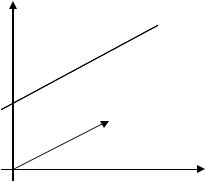
1.4. Уравнение прямой в отрезках
П. заданы отрезки а 0,b 0 , которые отсекает прямая на осях координат.
|
x |
|
y |
1 |
(4) – |
|
a |
b |
|
||
|
|
|
|
||
|
|
|
|
|
|
Уравнение (4) называется уравнением прямой в отрезках.
Пример 3. Записать уравнение прямой в отрезках, проходящей через точку А(2; -1) и отсекающей от положительной полуоси Оу отрезок вдвое больший, чем на положительной полуоси Ох.
b |
|
0 |
a |
|
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Generated by Foxit PDF Creator © Foxit Software |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
http://www.foxitsoftware.com |
For evaluation only. |
|||||
|
|
|
|
|
1.5.Каноническое и параметрическое уравнения прямой |
|
|
|||||||||||||||||||||||
|
|
Любой |
ненулевой |
|
|
|
|
вектор, |
|
|
|
|
|
|
|
|||||||||||||||
параллельный данной прямой, называется |
|
|
|
|
|
|
|
|||||||||||||||||||||||
направляющим вектором прямой. |
|
|
|
|
|
|
|
|
у |
|
|
|
|
|
||||||||||||||||
|
|
Запишем |
уравнение |
|
|
прямой, |
|
М |
|
|
|
|
|
|||||||||||||||||
проходящей через |
данную точку |
М0(x0;y0) |
|
|
|
|
|
|
||||||||||||||||||||||
(опорная точка) и имеющей заданный |
|
М0 |
|
|
|
|
|
|||||||||||||||||||||||
направляющий вектор |
|
|
(l; m) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
Очевидно, что т. М(х, |
у) |
лежит |
на |
|
s |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
указанной прямой M 0 M (x x0 ; y y0 ) |
и |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
(l; m) |
коллинеарные, а следовательно, |
их |
|
|
|
|
|
|
|
|||||||||||||||||||
|
s |
|
|
|
|
|
|
|
||||||||||||||||||||||
координаты должны быть пропорциональны. |
|
|
|
|
|
|
|
|||||||||||||||||||||||
Т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
х х0 |
|
y y0 |
|
|
(5) – |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
искомое каноническое уравнение |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
прямой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Если отношения в каноническом уравнении приравнять к параметру t ( t ) => |
||||||||||||||||||||||||||||
|
|
|
|
|
|
x x0 |
l t |
|
|
|
|
|
|
(6) – параметрическое уравнение прямой. |
|
|
||||||||||||||
|
|
|
|
|
|
|
m t |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
y y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.6. Общее уравнение прямой |
|
|
|
|
|
||||||||
|
|
Наиболее общим способом задать уравнение прямой является уравнение 1-й степени с |
||||||||||||||||||||||||||||
двумя переменными: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ах + Ву + С = 0 |
(7) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
в котором А и В не равны нулю одновременно, т.е. А2 + В2 0. |
|
|
|
|
|
|||||||||||||||||||||||
|
|
Частные случаи уравнения (5): |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1. |
В 0, тогда |
|
|
|
y |
A |
|
x |
C |
|
Это уравнение (1), в котором k |
A |
;b |
C |
|
|||||||||||||||
|
|
|
|
|
B. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
B. |
|
|
|
B |
||||||
|
|
Если A 0, С=0, тогда |
|
|
|
|
|
|
|
y=kx (прямая проходит через начало координат); |
|
|
||||||||||||||||||
|
|
|
А=0, С 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
у=b –прямая параллельна оси Ох; |
|
|
|
|
|
||||||||
2. |
В=0, А 0, тогда |
x |
C |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
||
|
|
С 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
х=а – прямая параллельна оси Оу; |
|
|
|
|
|
|||||||||
|
|
С=0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
х=0 – уравнение оси Оу. |
|
|
|
|
|
|||||||||
Таким образом уравнение (7) при любых допустимых значениях А, В, С есть уравнение некоторой прямой линии на плоскости Оху. Это общее уравнение прямой.
В отличие от уравнения пучка прямых, это уравнение включает в себя и уравнение любой вертикальной прямой, параллельной оси Оу.
29

|
|
Generated by Foxit PDF Creator © Foxit Software |
||
|
|
http://www.foxitsoftware.com For evaluation only. |
||
В.2. Взаимное расположение двух прямых на плоскости |
|
|||
2.1. Условия параллельности и перпендикулярности прямых |
||||
Пусть заданы две прямые: |
(1) |
у |
(2) |
|
y=k1x+b1 |
|
(1) |
||
(2) |
|
|
||
|
|
|||
|
|
|
|
|
y=k2x+b2.
Тогда угол между этими прямыми
( = 2- 1, |
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
, |
2 |
|
) определяется |
|
|
||||||||
2 |
|
2 |
|
|
||||||||||||
выражением: |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
х |
||
|
tg |
k2 k1 |
|
|
|
|
|
|
(8) |
|
||||||
|
|
|
|
|
|
|
|
О |
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 k1k2 |
|
k2 |
tg 2 ) |
|
|
|
|
|
|||||
(где |
|
|
|
Угол |
|
|
|
|||||||||
|
k1 |
tg 1 , |
|
|
||||||||||||
получается |
поворотом |
|
против |
часовой |
|
|
||||||||||
стрелки первой прямой до совпадения со второй.
Из выражения (8) условие параллельности двух прямых:
Равенство угловых коэффициентов является необходимым и достаточным условием
параллельности прямых: |
|
|
|
|
|
|
k1 |
k2 |
|
|
|
|
|
|
(9) |
||||||
а условие перпендикулярности – |
|
|
|
|
|
|
k1 k2 1 |
|
(10) |
||||||||||||
Т.о. для перпендикулярности прямых |
необходимо |
и достаточно, чтобы их угловые |
|||||||||||||||||||
коэффициенты были обратны по величине и противоположны по знаку. |
|||||||||||||||||||||
Если прямые заданы общими уравнениями |
|
|
А1 |
х + В1 |
у + С1 = 0, А2 х + В2 у + С2 = 0, |
||||||||||||||||
условие параллельности имеет вид: |
|
|
|
A1 |
|
B1 |
|
|
|
|
|
(11) |
|||||||||
|
|
|
A2 |
B2 |
|
|
|
||||||||||||||
а условие перпендикулярности – |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
А1 А2 + В1 В2 = 0. |
|
|
(12) |
||||||||||||||||||
Если прямые заданы каноническими |
или параметрическими уравнениями, то условия |
||||||||||||||||||||
параллельности: |
l1 |
|
m1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
l2 |
m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
перпендикулярности: |
l1 l2 |
m1 |
m2 0 ; |
|
|
|
|||||||||||||||
cos |
|
|
|
l1 l2 m1 m2 |
|
|
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
l 2 m2 |
l 2 m |
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
2 |
|
2 |
|
|
||||
Пример 4. Составить уравнения прямых, проходящих через т.А(1;1), одна из которых параллельна, а другая перпендикулярна прямой 3х – 2у – 2 = 0.
2.2. Точка пересечения прямых
Если прямые не параллельны, координаты точки их пересечения можно найти из решения системы уравнений:
A1 x B1 y C1 |
0, |
(13) |
|
0. |
|
A2 x B2 y C2 |
|
Точка пересечения в этом случае будет единственной.
2.3. Расстояние от точки до прямой
Если дано уравнение прямой в общем виде Ах + Ву + С = 0 и координаты точки М (хо,уо), не лежащей на этой прямой, то расстояние от точки М до прямой определяется выражением:
d |
|
Ax0 |
By0 |
C |
|
(14) |
|
|
|
||||||
|
|
|
|
|
|
||
|
|
A2 B2 |
|||||
|
|
|
|
||||
Пример 5. Найти расстояние от т.М(0;6) до прямой 3х + 4у + 6=0.
30
