
Матем_лекции_ 1сем_гр.,2621,2721
.pdf
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
Каждому действительному числу соответствует точка на числовой прямой, и наоборот, каждой точке числовой прямой соответствует действительное число.
Множество Х, элементы которого удовлетворяют неравенству a ≤ x ≤ b, называется отрезком [a; b]. Если элементы множества удовлетворяют неравенству a < x < b, то оно называется интервалом (а; b). Если же неравенствам a < x ≤ b, или a ≤ x < b , то – полуинтервалом (a; b], [a; b). Все указанные множества могут быть объединены одним термином – промежуток Х.
В.2. Абсолютная величина действительного числа. Окрестность точки
Абсолютной величиной (модулем) действительного числа х называется само число х, если х ≥ 0, и противоположное число –х, если х < 0, т.е.
х, |
|
х 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|x| = |
х, |
х 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Свойства абсолютных величин: |
1) |x + y| ≤ |x| + |y|; |
2) |x – y| ≥ |x| – |y|; |
|
||||||||||||||
|
3) |x∙y| ≤ |x|∙|y|; |
4) |
|
х |
|
|
|
|
х |
|
|
|
|
. |
|
||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
у |
|
|
у |
|
|
|
|
|||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Абсолютная величина разности двух чисел |x – а| означает |
. |
|
|x – а| |
. |
|
||||||||||||
расстояние между точками х и а числовой прямой (и для x < a, и |
|
|
|
|
|
|
|
|
|
|
х |
||||||
для х > а). |
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
а |
||
Поэтому, например, решениями неравенства |x – а|< ε (ε>0) |
|
|
|
|
|x – а|< ε |
|
|||||||||||
будут точки интервала (а – ε; а + ε), удовлетворяющие |
|
|
∙ |
|
|
|
∙ |
∙ |
х |
||||||||
неравенству а – ε < x < а + ε. |
|
|
а – ε |
|
а |
а + ε |
|||||||||||
Любой интервал, содержащий точку а, называется окрестностью точки а. Интервал (а – ε; а + ε) (т.е. множество точек х, удовлетворяющих неравенству |x –
а|< ε (ε>0)) называется ε – окрестностью точки а.
В.3. Определение функции
Постоянной величиной называется величина, сохраняющая одно и то же значение. Если величина сохраняет одно и то же значение лишь в условиях данного процесса,
то в этом случае она называется параметром.
Переменной называется величина, которая может принимать различные числовые значения.
Например, при равномерном движении s = v∙t: s и t – переменные, v – параметр. Если по некоторому закону f каждому элементу х из множества Х ставится в
соответствие вполне определенный элемент у из множества Y (т.е. х Х f !y Y ), то говорят, что на множестве Х задана функция y = f(x).
При этом х называется независимой переменной, у – зависимой, f – законом соответствия; множество Х называется областью определения, Y – областью значений
функции.
Замечание. Если множество Х специально не оговорено, то под областью определения понимают область допустимых значений х, т.е. таких значений переменной х, при которых выражение y = f(x) имеет смысл.
Способы задания функций:
а) Аналитический способ (функция задана формулой вида y = f(x)).
б) Табличный способ (функция задается таблицей, содержащей значения аргумента х и соответствующие значения функции y = f(x)).
в) Графический способ (функция задана графиком, т.е. множеством точек (х;у) плоскости, абсциссы которых есть значения аргумента х, а ординаты – соответствующие им значения функции y = f(x)).
г) Словесный способ (функция описывается правилом составления, например, функция Дирихле равна 1, если х – рационально, и 0, если х – иррационально).
41
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
Основные свойства функций: 1. Четность и нечетность.
Функция y = f(x) называется четной, если для любых значений х из области
определения ( х Х ) f(– x) = f(x). График четной функции симметричен относительно оси Оу. Например, функция у = х2 – четная, т.к. f(– x) = (–х)2 = х2 = f(x).
Функция y = f(x) называется нечетной, если х Х f(–x) = – f(x). График нечетной
функции симметричен относительно начала координат. Например, функция у = х3 –
нечетная, т.к. f(– x) = (–х)3 = –х3 = –f(x).
Если функция не является ни четной, ни нечетной, то она называется функцией общего вида. Например, функция у = х2 + х5 – общего вида.
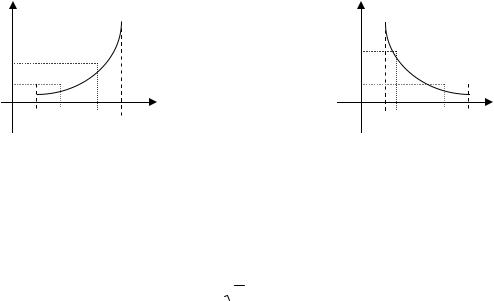
2. Монотонность. Функция y = f(x) называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции. Т.е. пусть х1, х2 Х и х2 > х1, тогда функция возрастает на промежутке Х, если f(х2) > f(х1) и убывает, если f(х2) < f(х1).
y |
|
y |
|
f(x1) |
|
f(x1) |
|
f(x2) |
x |
f(x2) |
х2 b x |
О а х1 х2 b |
О а х1 |
Возрастающие и убывающие функции называются монотонными.
3. Ограниченность. Функция y = f(x) называется ограниченной на промежутке Х, если существует такое положительное число М > 0, что |f(x)| ≤ M х Х .
Например, функция y = sinx ограничена на всей числовой оси, т.к. |sinx| ≤ 1 х R . 4. Периодичность. Функция y = f(x) называется периодической с периодом Т≠0,
если для любых х из области определения функции f(x+Т) = f(x).
Например, функция y = cosx имеет период Т = 2π, т.к. для х R cos(x+2π )= cosx.
В.4. Основные элементарные функции и их свойства (см. приложение)
1.Степенная функция: y = xn; y = x-n; y = n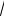 x .
x .
2.Показательная функция: y = ax.
3.Логарифмическая функция: y = logax.
4.Тригонометрические функции: y = sin x; y = cos x; y = tg x; y = ctg x.
5.Обратные тригонометрические функции: y = arcsin x; y = arccos x; y = arctg x; y = arcctg x.
В.5. Элементарные функции
Функция называется явной, если она задана формулой вида y = f(x) (правая часть не содержит зависимой переменной).
Функция называется неявной, если она задана уравнением F(x, y) = 0, не разрешенным относительно зависимой переменной.
Пусть функция y = f(x) – функция от независимой переменной х с областью определения Х и областью значений Y. Поставим в соответствие у Y единственное
значение х X , при котором f(x) = y. Тогда полученная функция х = φ(у), определенная
на промежутке Y с областью значений Х, называется обратной (обратную функцию также обозначают y = f -1(x)).
Для любой строго монотонной функции существует обратная функция. Графики взаимно обратных функций симметричны относительно прямой у = х (биссектрисы 1-го и 3-го координатных углов).
Пример 2. Для функции у = 3х найти обратную.
Функция у = 3х монотонная (возрастающая), следовательно, она имеет обратную. Для того чтобы получить формулу обратной функции выразим переменную х через у:
42
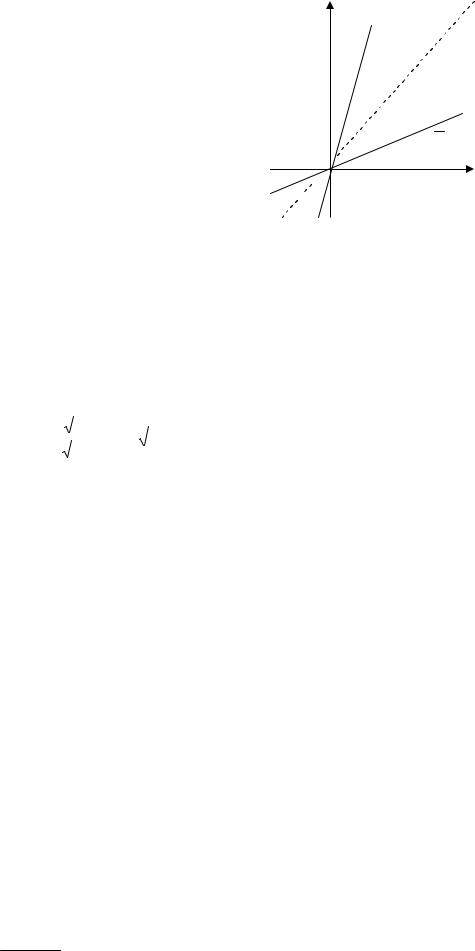
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
х |
1 |
у . А затем полученную формулу запишем в |
у |
у = х |
||||
|
||||||||
3 |
|
|
1 |
|
|
|
у = 3х |
|
|
|
|
|
|
|
|
||
привычном виде (поменяем х и у местами): |
у |
х |
- |
|
|
|||
|
|
|
||||||
|
|
|
3 |
|
|
|
|
|
это и есть обратная функция к данной.
у 1 х 3
 О х
О х
Пусть функция y = f(и) – функция переменной и определена на множестве U с областью значений Y, а переменная и – функция переменной х: и = φ(х), определена на множестве Х с областью значений U. Тогда заданная на множестве Х с областью значений Y функция y = f[φ(х)] называется сложной функцией (композицией функций,
функцией от функции).
Например, у = cos(x2+x) – сложная функция, т.к. ее можно представить в виде , у = cosи, где и = x2+x.
Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.
|
|
|
|
|
|
|
|
|
3 |
|
х tg 2 x |
|
|
|
|||
|
|
|
|
|||||
Например, функция у |
|
|
|
|
|
|
lg x 5 – элементарная (пример неэлементарной |
|
|
|
|
|
5 |
||||
|
x 34x |
|||||||
функции у = |x|). |
|
|
|
|
||||
|
|
|
|
|
|
|||
Классификация функций. Элементарные функции делятся на:
1)Алгебраические (полученные с помощью конечного числа алгебраических действий над аргументом). К ним относятся:
целая рациональная функция (многочлен): у а0 хn a1xn 1 ... an 1x an ;
дробно-рациональная функция – отношение двух многочленов;
иррациональная функция (в составе операций над аргументом есть извлечение корня).
2)Неалгебраические (или трансцендентные). К ним относятся: показательная,
логарифмическая, тригонометрические, обратные тригонометрические.
В.6. Интерполирование функций
Интерполирование – приближенное вычисление неизвестных значений функции по известным ее значениям в заданных точках.
Наиболее простым является линейное интерполирование, при котором допускается, что приращение функции пропорционально приращению аргумента.
Пример 3. Значение функции известно в точках a и b. С помощью линейной интерполяции найти значение функции в точке с.
а |
f(a) |
b |
f(b) |
c |
2 |
2,42 |
2,04 |
2,88 |
2,008 |
Решение. Значение с лежит между а и b. Формула линейного интерполирования:
f(c) f(a) + |
c a |
f |
, где h = b – a, f = f(b) – f(a). |
|
|||
|
h |
|
|
Подставляя в формулу известные значения из таблицы, получим:
f(2,008) 2,42 + 2,008 2 0,46 = 2,512.
0,04
Ответ. f(2,008) 2,512.
43
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
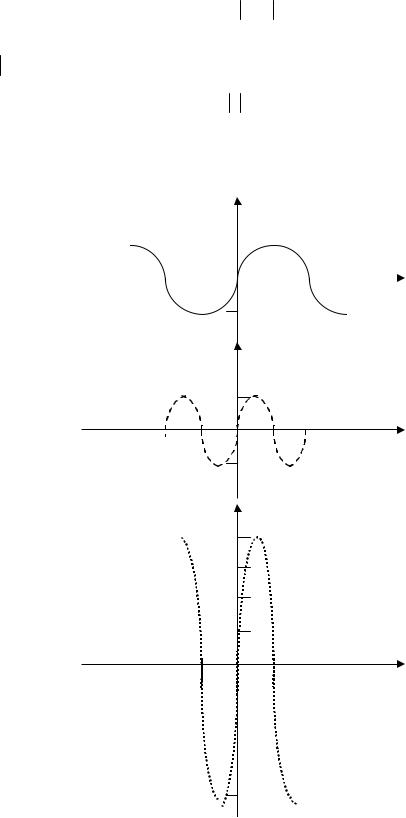
В. 7. Преобразование графиков
Пусть задан график функции y = f(x). Тогда справедливы следующие утверждения:
1.График функции y = f(x+a) есть график y = f(x), сдвинутый на а единиц параллельно оси Оy (вдоль оси Oх); при a > 0 – влево, при a < 0 – вправо.
2.График функции y = f(x)+b есть график y = f(x), сдвинутый b единиц параллельно оси Оx (вдоль оси Oy); при b > 0 – вверх, при b < 0 – вниз.
3.График функции y = mf(x) (m≠0) есть график y = f(x), растянутый при m > 1 в m раз или сжатый при 0 < m <1 в m раз вдоль оси Oy. При m < 0 график функции y = mf(x) есть зеркальное отображение графика y = -mf(x) от оси Ox.
4.График функции y = f(kx) (k≠0) есть график y = f(x), сжатый при k > 1 в k раз или растянутый при 0 < k < 1 в k раз вдоль оси Ox. При k < 0 график функции y = f(-kx) есть зеркальное отображение графика y = f(kx) от оси Oy.
5.График функции у f (x) получается из графика функции y = f(x), если оставить на
месте ту часть, где f(x) ≥ 0 и симметрично отобразить относительно Ох часть f(x)˂ 0:
f (x) |
|
f (x), |
f (x) 0 |
|
|
. |
|
|
|
f (x), |
f (x) 0 |
|
|
6. График функции y f ( x ) совпадает с графиком y = f(x) на множеств неотрицательных
значений аргумента и симметричен ему относительно Оу на множестве отрицательных значений аргумента.
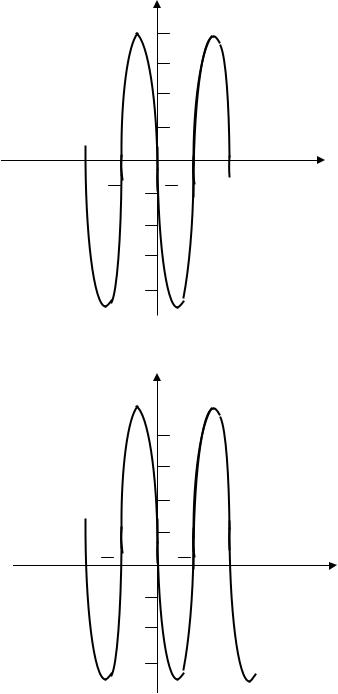
Пример 4. Построить график функции у = –4∙sin2x + 1.
Решение. 1) Сначала построим график функции у = sinx.
|
|
у |
|
|
||||
|
|
1 |
|
|
|
|
х |
|
|
|
|
|
|
|
|||
|
|
О |
|
|||||
|
|
|
||||||
|
|
|
|
|
|
|
||
-π - |
-1 |
|
|
π |
||||
|
|
|||||||
22
2)Сжатием графика в 2 раза вдоль оси Ох получаем график функции у=sin2x.
у
|
|
О |
1 |
|
|
х |
|
|
|
|
|
||
-π - |
|
|
|
π |
||
|
|
|
||||
|
|
|
22
3)Растянем график у = sin2x вдоль оси Оу в 4 раза и получим график функции у = 4sin2x.
у
4
|
|
О |
1 |
|
|
х |
||
|
|
|
|
|
|
|||
-π - |
|
|
|
|
|
π |
||
|
|
|
|
|
||||
|
|
|
|
|||||
2 |
|
|
|
2 |
|
|
||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
44
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
-4
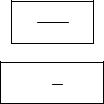
4) Зеркально отобразив график от оси Ох, получим у = –4sin2x.
у
4
О |
1 |
х |
|
||
-π - |
|
π |
2 |
2 |
|
-4
5) Сдвинем полученный график на 1 единицу вверх параллельно оси Оу. Таким образом
график функции у = – 4∙sin2x + 1 имеет вид:
у
5
1
π |
|
О |
|
π |
х |
|
2 |
2 |
|||||
|
|
|
|
-3
Тема 2. ПРЕДЕЛЫ И НЕПРЕРЫВНОСТЬ В.1. Предел числовой последовательности
Если по некоторому закону каждому натуральному числу n поставлено в соответствие вполне определенное число an, то говорят, что задана числовая последовательность {an}:
a1, a2,…,an… .
Другими словами, числовая последовательность – это функция натурального аргумента an=f(n).
Числа a1, a2,…,an называются членами последовательности, а число an – общим или n-м членом данной последовательности.
Пример 1: а) 2, 4, 6, …2n, … (монотонная неограниченная); б) 1, 0, 1, 0, … (немонотонная ограниченная);
|
3 |
|
|
2 |
|
5 |
|
4 |
|
|
|
( 1) |
n |
|
|
|
|
|
|
|
|
|
|||||||||
в) 0, , |
|
|
, |
|
, , …, |
|
|
|
, … - немонотонная, ограниченная. Изобразим её точками |
||||||
3 |
|
1 |
n |
|
|
||||||||||
2 |
|
4 |
5 |
|
|
|
|
|
|
||||||
числовой оси. |
С ростом n последовательность как угодно близко приближается к 1. При этом |
||||||||||||||
45

a1 1 |
|
1, |
|
a2 |
1 |
|
|
1 |
, |
|
a3 |
1 |
|
|
1 |
, … , |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
||
Generated by Foxit PDF Creator © Foxit Software http://www.foxitsoftware.com For evaluation only.
an |
1 |
|
|
1 |
, … Т.е. с ростом n расстояние |
|
an 1 |
|
будет |
|
|
|
|||||||
|
n |
||||||||
|
|
|
|
|
|
|
|
|
меньше любого, сколь угодно малого числа.
Число А называется пределом числовой последовательности {an}, если для любого сколь угодно малого положительного числа > 0 найдется такой номер N( ), зависящий от , что для
всех членов данной последовательности с номерами n > N( ) верно неравенство |
an - A < . |
Предел числовой последовательности обозначается lim an A или an |
. Используя |
n |
n |
следующие логические символы (кванторы): (любой), (существует), (равносильность или эквивалентность), определение предела можно записать в виде:
(A = lim an) ( > 0 N( ) : n > N( ) an – A < )
n
Последовательность, имеющая предел, называется сходящейся, в противном случае –
расходящейся.
Смысл определения: для достаточно больших n члены последовательности {an} сколь угодно мало отличаются от числа А.
В.2. Предел функции
Число А называется пределом функции y = f(x) при х, стремящемся к бесконечности
(пределом функции в бесконечности), если для любого > 0 найдется такое S > 0, что для всех
х > S верно неравенство f(x) – A < . |
f(x) = A, или f(x) A при х ( f (x) A ). |
Предел функции обозначается lim |
|
x |
x |
(A = lim f(x) ( > 0 S = S( ) > 0 : x : x > S f(x) – A < ).
x
Смысл определения: при достаточно больших по модулю значениях х значения функции f(x) как угодно мало отличаются от числа А.
Число А называется пределом функции f(x) при х х0, (в точке х0), если для
> 0 = ( ) > 0 : x x0, х – x0 < выполняется неравенство f(x) – A < .
Смысл определения: для всех значений х, достаточно близких к х0, значения f(x) как угодно мало отличаются от числа А.
Замечание 1. Определение предела не требует существования функции в самой точке х0, поскольку предполагается, что х стремится к х0, но не достигает значения х0. Поэтому наличие или отсутствие предела при х х0 определяется поведением функции в окрестности точки х0, но не связано с существованием функции в самой точке х0.
Замечание 2. Если при х х0 х принимает только значения, меньшие х0, и при этом функция f(x) стремится к некоторому числу А, то говорят об одностороннем пределе функции
слева: |
|
|
lim |
f(x) = A |
. |
|
|
|
|
|
x x0 0 |
|
|
|
|
Аналогично, если при х х0 |
х |
> х0, то говорят об одностороннем пределе функции |
|||||
справа, т.е: |
|
|
lim |
f(x) = A |
|
|
|
|
|
|
x x0 0 |
|
|
|
|
При этом, если lim |
f(x) = lim |
|
f(x) = А, то lim f(x) = A. |
|
|||
x x0 0 |
x x0 0 |
|
|
x x0 |
|
||
|
В. 3. Бесконечно малые величины |
|
|||||
Функция (x) называется бесконечно малой величиной при х х0 |
(при х ), если ее |
||||||
предел равен нулю: |
|
|
lim |
(x) = 0. |
|
||
x x0 ( )
Например, функция y 1 - б.м.в. при х , у х2 - б.м.в. при х 0. x2
Связь бесконечно малых величин с пределами функций определяется теоремами:
Теорема: Если lim f(x) = A, то функцию f(x) можно представить в виде суммы
x x0 ( )
f(x) = A + (x), где (x) – бесконечно малая при х х0 ( ).
46
Generated by Foxit PDF Creator © Foxit Software
http://www.foxitsoftware.com For evaluation only.
Обратная теорема: Если функцию f(x) можно представить как сумму числа А и бесконечно малой (x) при х х0 ( ), то число А есть предел этой функции при х х0 ( ), т.е.
lim f(x) = A.
x x0 ( )
Свойства бесконечно малых величин:
1.Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.
2.Произведение бесконечно малой величины на ограниченную функцию есть величина бесконечно малая.
3.Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.
Замечание. Свойство 3 не рассматривает предел отношения двух бесконечно малых (x) и
(x) из-за его неопределенности. Этот предел |
lim |
(x) |
|
может быть равен нулю, числу А 0 |
||
(x) |
||||||
|
x x0 ( ) |
|
||||
или бесконечности . |
В первом случае (x) |
называется |
бесконечно малой более высокого |
|||
порядка малости чем (x). Это записывается так: (x) = ( (x)) при х х0 ( ), т.е. “ (x) есть О малое от (x)”. Во втором случае (x) и (x) одного порядка малости (“ (x) есть О большое от
(x)” или |
(x) = O( (x))). В третьем случае (x) более низкого порядка малости чем (x). При |
||
lim |
(x) |
=1 (x) и (x) называются эквивалентными и пишут (x) (x). |
|
(x) |
|||
x x0 ( ) |
|
||
В. 4. Бесконечно большие величины
Функция f(x) называется бесконечно большой величиной при х х0, если для M > 0 найдется такое > 0 ( (M)), что для x x0, х – x0 < будет верно: f(x > M. (Т.е.
lim f (x) ).
x x0 ( )
Например, функция y |
1 |
- б.б.в. при х 0, |
у х2 |
- б.б.в. при х . |
|
x2 |
|||||
|
|
|
|
Замечание. Бесконечно большая величина есть функция неограниченная при х х0 ( ). В то же время не всякая неограниченная функция является бесконечно большой. Например, функция y = x sin x является неограниченной, но не бесконечно большой, т.к. с ростом х функция все время колеблется, переходя от положительных к отрицательным значениям и наоборот.
Свойства бесконечно больших величин:
1.Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.
2.Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая.
3.Частное от деления бесконечно большой величины на функцию, имеющую предел в точке х0, есть величина бесконечно большая.
Связь между бесконечно малыми и бесконечно большими величинами устанавливает следующая теорема:
Теорема: Если (x) есть бесконечно малая при х х0 ( ), то функция f(x) = |
1 |
является |
|
||
|
(x) |
|
бесконечно большой при х х0 ( ). Обратно, если функция (x) есть бесконечно большая при х
х0 ( ), то функция f(x) = |
1 |
есть бесконечно малая при х х0 |
( ). |
|
|
||||
|
|
(x) |
|
|
В. 5. Основные теоремы о пределах. Признаки существования предела |
||||
Пусть f(x) и (x) – функции, для которых существуют пределы при х х0 ( ): |
||||
А lim |
f (x) , B |
lim (x) . |
|
|
x x0 ( ) |
|
x x0 ( ) |
|
|
Тогда имеют место следующие теоремы о пределах:
1.Функция не может иметь более одного предела.
2.Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций:
47
Generated by Foxit PDF Creator © Foxit Software http://www.foxitsoftware.com For evaluation only.
lim [ f (x) (x)] A B .
x x0 ( )
3.Предел произведения конечного числа функций равен произведению пределов этих функций:
lim [ f (x) (x)] A B .
x x0 ( )
В частности, постоянный множитель можно выносить за знак предела:
lim |
(С f (x)) C lim |
f (x) C A . |
x x0 ( ) |
x x0 ( ) |
|
4. Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю):
|
|
lim |
f (x) |
|
A |
(B 0) |
|
|
|
|
|||
|
|
x x0 ( ) (x) |
B |
|||
5. |
Если lim |
f (u) A, lim (x) u0 , то предел сложной функции: |
||||
|
u u0 |
x x0 |
|
|
||
lim f [ (x)] A .
x x0
6.Если в некоторой окрестности точки х0 (или при достаточно больших х) f(x) < (x), то:
lim f (x) lim (x)
x x0 ( ) x x0 ( )
Использовать эти теоремы для выяснения существования предела не всегда удобно. Проще сделать это с помощью признаков существования предела:
Теорема 1. Если числовая последовательность {an} монотонна и ограничена, то она имеет предел.
Возможны два случая: а) последовательность неубывающая и ограничена сверху – a1 a2 a3 … an …M; б) последовательность невозрастающая и ограничена снизу – a1 a2 a3 … an
…M;
Теорема 2. Если в некоторой окрестности точки х0 (или при достаточно больших х) функция f(x) заключена между двумя функциями φ(х) и (х), имеющими одинаковый предел А при х х0 ( ), то функция f(x) имеет тот же предел А.
В. 6. Замечательные пределы. Задача о непрерывном начислении процентов Первым замечательным пределом является:
lim sin x 1
x 0 x
Вторым замечательным пределом является:
lim (1 1)n е
n n
где е 2,718281…– число Эйлера, которое является основанием для натуральных логарифмов. Этот предел имеет записи:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
lim(1 |
)x е |
|
|
или |
|
|
|
|
|
|
|
|
|
|
lim(1 y) |
y |
|
е. |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Пример 2. lim |
1 cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
x 0 |
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для |
раскрытия |
подобных |
|
|
неопределенностей |
|
|
|
|
|
|
используется |
|
первый |
замечательный |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
предел: |
|
1 cos x |
|
|
|
|
|
|
|
2sin |
2 |
x |
|
|
|
|
|
|
|
2 sin |
x |
sin |
|
x |
|
|
|
|
2 |
|
|
|
|
sin |
x |
|
|
sin |
x |
|
|
1 |
|
1 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
2 |
||||||||||||||||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
lim |
|
|
2 |
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
lim |
|
2 |
|
lim |
|
|
|
|
|
1 1 |
|
|
|||||||||||||||||||||||||||
|
2 |
|
|
2 |
|
|
|
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
x 0 x |
|
|
|
|
x 0 x |
|
|
|
|
|
|
|
x 0 |
|
4 |
|
|
|
|
|
|
|
|
|
4 x 0 |
|
|
x |
|
x 0 |
x |
2 |
|
2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
5 |
|
3x |
|
|
|
|
|
|
|
|
|
5 |
x |
3 5 |
|
|
|
|
|
|
5 |
x |
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Пример 3. lim(1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
) |
|
|
|
lim(1 |
x |
) |
|
|
|
|
lim[(1 |
x |
|
) |
|
] e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
x |
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 4. lim(1 3y) |
|
|
lim(1 3y) |
|
( 2) 3 lim[(1 3y) |
|
] 6 e 6 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
y |
3 y |
3 y |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
y 0 |
|
|
|
|
|
|
|
|
y 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Рассмотрим задачу о непрерывном начислении процентов. Первоначальный вклад в банк составил Q0 денежных единиц. Банк выплачивает ежегодно p% годовых. Необходимо найти размер вклада через t лет.
48

|
|
|
|
|
|
|
|
|
Generated by Foxit PDF Creator © Foxit Software |
|||
|
|
|
|
|
|
|
|
|
http://www.foxitsoftware.com |
For evaluation only. |
||
|
|
При p% годовых размер вклада ежегодно будет увеличиваться в |
(1 |
p |
) раз, т.е. Q1 = |
|||||||
|
|
|||||||||||
|
|
p |
|
|
p |
|
|
p |
|
100 |
|
|
Q0 |
(1 |
) , Q2 |
= Q0 (1 |
)2 , …, Qt = Q0 |
(1 |
)t . |
|
|
|
|||
|
|
|
|
|
|
|||||||
|
100 |
|
100 |
|
100 |
|
|
|
|
|||
|
|
Если начислять проценты по вкладам не один раз в году, а n раз, то при том же ежегодном |
||||||||||
приросте p% процент начисления за |
1 |
-ю часть года составит |
p |
% , а размер вклада за t лет при nt |
|
n |
|
n |
|
начисления составит: |
|
|
|
|
Qt = Q0 (1 p )nt .
100n
Пусть проценты по вкладу начисляются каждое полугодие (n = 2), ежеквартально (n = 4), ежемесячно (n = 12), каждый день (n =365), каждый час (n = 8760), и тд., непрерывно (n ). Тогда размер вклада за t лет составит:
|
|
p |
)nt Q0 lim[(1 |
p |
100n |
|
tp |
|
pt |
||||
Qt |
lim[Q0 (1 |
) |
|
p |
] |
|
Q0e |
|
. |
||||
|
100 |
100 |
|||||||||||
100n |
100n |
|
|||||||||||
|
n |
n |
|
|
|
|
|
|
|
|
|||
Эта формула |
выражает показательный |
(экспоненциальный) закон роста (p > 0) или |
|||||||||||
убывания (p < 0). Она может быть использована при непрерывном начислении процентов. Пример 5. П. Q0 = 6 млн.руб., р = 10%. Найти размер вклада через 5 лет при:
А) ежегодном; Б) поквартальном, В) непрерывном начислении процентов.
Решение. |
А) Q5 = 6 (1 |
|
10 |
)5 |
9,663(млн.руб) . |
|||
100 |
||||||||
|
|
|
|
|
|
|||
|
Б) Q5 = 6 (1 |
10 |
)5 4 9,832(млн.руб) . |
|||||
|
4 100 |
|||||||
|
10 5 |
|
||||||
|
|
|
|
|
||||
|
В) Q5 = 6 е |
100 |
|
|
9,895(млн.руб) . |
|||
В.7. Непрерывность функции
Функция f(x) называется непрерывной в точке х0, если она удовлетворяет следующим условиям:
1)она определена в точке х0,, т.е. существует f(х0);
2)она имеет конечный предел функции при х х0 ( lim f (x) );
x x0
3) этот предел равен значению функции в точке х0, т.е. lim f (x) f (x0 )
x x0
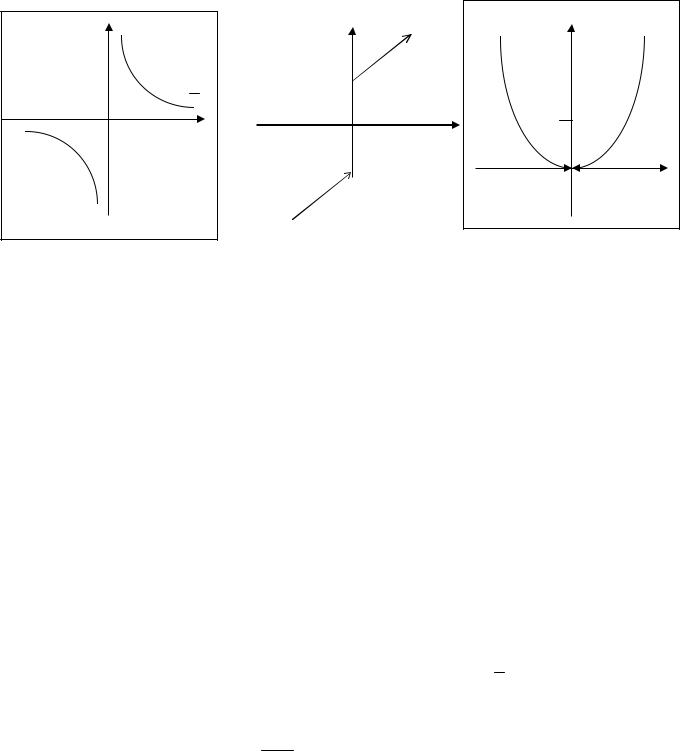
Пример 6. А) Функция y |
1 |
в точке х = 0 не является непрерывной (нарушено 1-е |
|
x |
|||
|
|
||
условие). |
|
||
x 1, x 0
Б) Функция, заданная выражением: y в точке х = 0 не является непрерывной
x 1, x 0,
из-за отсутствия предела при х 0, хотя существуют пределы слева и справа (нарушено 2-е условие).
|
х |
2 |
, |
х 0, - не является непрерывной, т.к. нарушено 3-е условие. |
В) у |
|
|||
1, |
|
|
х 0 |
|
Г) Функция y = x2 является непрерывной в точке х = 0.
49
у
y 1 x
О х
x 1, x 0 y
x 1, x 0
x
Generated by Foxit PDF Creator © Foxit Software http://www.foxitsoftware.com For evaluation only.
y |
|
|
|
|
у |
|
|
|
|
|
|
1_ |
|
х |
2 |
, |
х 0, |
у |
|
||||
|
1, |
|
|
х 0 |
|
1
1_
О х
Непрерывность функции f(x) в точке х0 можно записать и так:
lim |
f (x) f (lim x) |
x x0 |
x x0 |
т.е. для непрерывной функции возможна перестановка символов предела и функции. Другое определение непрерывности: функция y = f(x) называется непрерывной в точке х0,
если она определена в этой точке и бесконечно малому приращению аргумента соответствует
бесконечно малое приращение функции: |
lim y 0 |
|
x 0 |
Оба определения равносильны.
Точка х0 называется точкой разрыва функции f(x), если эта функция в данной точке не является непрерывной. Существует две разновидности точек разрыва.
Точка разрыва 1-го рода: существуют конечные односторонние пределы функции слева и справа при х х0, не равные друг другу.
x 1, x 0
В качестве примера можно указать точку х = 0 для функции y .
x 1, x 0
К точкам разрыва 1-го рода относятся и точки устранимого разрыва: односторонние пределы функции равны друг другу, но не равны значению функции в точке. Пример – точка х = 0
|
х |
2 |
, |
х 0, |
для функции у |
|
|||
1, |
|
|
х 0 |
|
Точка разрыва 2-го рода: хотя бы один из односторонних пределов равен бесконечности или не существует.
В качестве примера можно указать точку х = 0 для функции y 1 . x
Свойства функций непрерывных в точке:
1.Если функции f(x) и (х) непрерывны в точке х0, то их сумма f(x) + (х),
произведение f(x) (х) и частные f (x) ( (х) 0) являются функциями, непрерывными в точке
(x)
х0.
2.Если функция y = f(x) непрерывна в точке х0 и f(x0) > 0, то существует такая окрестность точки x0, в которой и f(x) > 0.
3.Если функция y = f(u) непрерывна в точке u0, а функция u = (х) непрерывна в точке х0, то сложная функция y = f[ (х)] непрерывна в точке х0 .
Функция y = f(x) называется непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка.
Свойства функций непрерывных на отрезке:
1.Если функция y = f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке.
2.Если функция y = f(x) непрерывна на отрезке [a, b], она достигает на этом отрезке наименьшего значения m и наибольшего значения M.
50
