
lin2011
.pdf
A |
|
1 |
|
A |
1 |
|
AA E, |
|||
| A | |
| A | |
|||||||||
|
|
|
|
|||||||
1 |
|
A A |
E. |
|
||||||
|
|
|
|
|
||||||
|
| A | |
|
|
|
|
|||||
Тем самым матрица, определенная равенством (3.3), действительно является обратной. Докажем единственность обратной матрицы. Предположим, что
нашлись две обратные матрицы А1-1 и А2-1. Тогда, умножив равенство
АА1-1 = Е
слева на А2-1, получим:
A |
1 AA 1 |
A 1E |
A 1. |
2 |
1 |
2 |
2 |
Отсюда, в силу того, что А2-1А = Е, вытекает равенство
А1-1 = А2-1.
Пример 3. Найдем обратную матрицу для
1 3 4 A 0 2 3 .
1 2 1
Для нахождения присоединенной матрицы найдем сначала все алгебраические дополнения:
A11 |
|
2 |
3 |
8; |
A12 |
|
0 |
|
3 |
|
3; |
A13 |
0 |
2 |
|
|
2; |
||||||
|
2 |
1 |
|
|
1 |
|
1 |
|
1 |
|
|
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
A21 |
|
4 |
|
5; |
A22 |
|
1 |
|
4 |
|
|
3; |
A23 |
|
1 |
|
3 |
|
1; |
||||
|
3 |
|
|
|
|
|
|
|
|
||||||||||||||
|
2 |
1 |
|
|
1 |
|
1 |
|
|
|
1 |
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
A31 |
|
4 |
|
|
17; |
A32 |
|
1 |
4 |
|
3; A33 |
|
1 |
|
3 |
|
2. |
||||||
3 |
|
|
|
|
|
|
|
||||||||||||||||
2 |
3 |
|
|
|
|
0 |
3 |
|
|
0 |
|
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно (напомним, что алгебраические дополнения для элементов строк в присоединенной матрице надо расположить в соответствующем столбце),
8 5 17 A 3 3 3 .
2 1 2
Поскольку |A| = 1· A11 + 0· A12 + 1· A13 = - 9, получаем:
|
|
|
|
|
8 |
5 |
|
17 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
9 |
|
9 |
|
|
|
|||||||
A 1 |
1 |
|
A |
1 |
|
1 |
|
1 |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
| A | |
|
|
3 |
|
3 |
3 |
|
|
|||||||||
|
|
|
|
|
2 |
|
1 |
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
9 |
|
9 |
9 |
|
|||||||||
43

Упражнение 2. Найти обратную матрицу для
1 0 4 A 2 2 3 .
1 0 1
Решение.
Проверим невырожденность матрицы А:
| A | 1 2 4 ( 2) 6 0,
следовательно, обратная матрица существует. Вычислим алгебраические дополнения к элементам матрицы А:
A11 |
2 |
|
3 |
|
|
2, A12 |
|
2 |
|
3 |
|
|
1, A13 |
2 |
2 |
|
|
2, |
|||||
0 |
|
1 |
|
|
|
1 |
|
1 |
|
|
1 |
0 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
A21 |
|
4 |
|
0, |
A22 |
|
1 |
|
4 |
|
3, |
A23 |
|
|
1 |
0 |
|
0, |
|||||
|
0 |
|
|
|
|
|
|
|
|||||||||||||||
|
0 |
1 |
|
|
|
1 |
|
1 |
|
|
|
1 |
0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
A31 |
|
|
4 |
|
8, |
A32 |
|
|
|
1 |
4 |
|
5, |
A33 |
|
1 |
0 |
|
2. |
||||
0 |
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
|
3 |
|
|
|
|
2 |
3 |
|
|
2 |
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Построим присоединенную матрицу: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
0 |
|
8 |
|
|
|
|
|
|
|
|
|
A 1 3 5 . 2 0 2
Используя теорему 3.3, находим обратную матрицу:
|
|
|
|
|
|
|
|
1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
8 |
3 |
|||
|
1 |
|
|
1 |
|
1 |
|||||
A 1 |
|
A |
1 |
3 |
5 |
||||||
| A | |
6 |
6 |
|||||||||
|
|
2 |
0 |
2 |
|||||||
|
|
|
|
|
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
3 |
|||
04
3
15 .
26
01
3
Упражнение 3. Доказать, что (АВ)-1 = В-1А-1.
Решение.
Пусть С = В-1А-1. Тогда, применяя свойство 1 произведения матриц, понятие единичной матрицы (лекция 1) и определение обратной матрицы, получим:
( AB)C A(BC) A(B(B 1 A 1)) A((BB 1) A 1) A(EA 1) AA 1 E; C( AB) (CA)B ((B 1 A 1 ) A)B (B 1( A 1 A))B (B 1E)B B 1B E.
Следовательно, матрица С = В-1А-1 удовлетворяет определению обратной матрицы для матрицы АВ. Значит, (АВ)-1 = В-1А-1.
44

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ
«Обратная матрица»
Задача 1.
Найти обратную матрицу для матрицы
А
1 1
2 4
и проверить выполнение условий А А-1 = А-1А = Е.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
Убедимся, что матрица А – невырожденная. А = 1·4 - 2·(-1) ≠ 0, следовательно, А-1 существует.
Вычислим алгебраические дополнения к элементам А:
A11 |
( |
1)1 1 |
4 |
4; |
A21 |
( 1)2 1 |
( |
1) |
1 ( |
1) |
1; |
A12 |
( |
1)1 2 |
2 |
1 |
2 |
2; A22 |
( |
1)2 2 |
1 |
1. |
|
Применим способ вычисления обратной матрицы:
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
1 |
4 |
1 |
|
|
|
|
|
|
A |
1 |
3 |
|
|
6 |
|
||||
|
|
|
|
|
|
|||||
|
6 |
2 |
1 |
|
1 |
|
1 . |
|||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
6 |
|
||
Не забудьте, что обратная матрица образована из алгебраических дополнений к элементам
транспонированной матрицы!
Найдем произведения А А-1 и А-1А:
|
|
|
|
2 |
|
|
1 |
2 |
1 |
|
1 |
1 |
|
|
|
|
||||
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
AA |
1 |
3 |
|
|
6 |
3 |
3 |
|
6 |
6 |
E; |
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
4 |
|
1 |
|
1 |
|
4 |
|
4 |
|
2 |
|
4 |
|
0 |
1 |
|||
|
|
|
|
|
||||||||||||||||
|
|
|
|
3 |
6 |
3 |
3 |
|
6 |
6 |
|
|
|
|
||||||
|
|
|
2 |
|
|
1 |
|
|
2 |
|
|
2 |
|
2 |
4 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
A |
1 |
A |
3 |
|
|
6 |
3 |
|
|
6 |
|
3 |
6 |
E. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
1 |
|
1 |
2 |
4 |
|
1 |
|
|
2 |
|
1 |
|
|
4 |
|
0 |
1 |
||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
3 |
6 |
|
|
3 |
6 |
3 |
6 |
|
|
|
|
|||||||||||||
Таким образом, найденная матрица А-1 отвечает определению обратной матрицы.
45
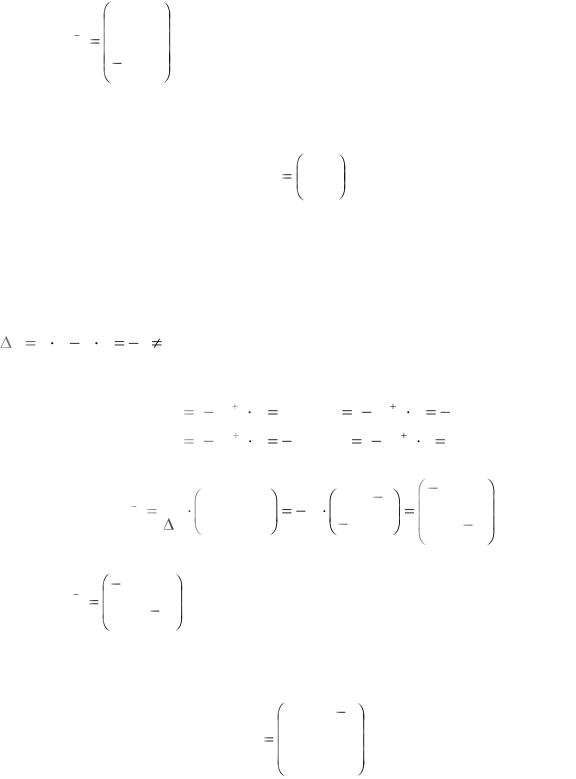
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
Ответ: A 1 |
3 |
|
|
6 . |
||
|
|
1 |
|
1 |
|
|
|
3 |
6 |
|
|||
Задача 2.
Найти обратную матрицу для матрицы
1 2
А3 4 .
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
A |
1 4 |
3 2 |
2 |
0. |
Следовательно, матрица А невырожденная, и обратная матрица существует. Вычислим алгебраические дополнения к элементам матрицы А:
A11 ( 1)1
A21 ( 1)2
Обратная матрица имеет вид:
|
A |
1 |
|
1 |
|
A11 |
|||
|
|
|
|
|
A |
A12 |
|||
|
|
|
|
|
|
|
|||
2 |
|
1 |
|
|
|
||||
Ответ: A 1 3 |
|
1 . |
|
||||||
|
2 |
|
|
|
2 |
|
|
|
|
1 |
4 |
4; A12 ( |
1)1 2 |
3 |
|
3; |
|
1 |
2 |
2; |
A22 |
( 1)2 |
2 1 |
|
1. |
|
A21 |
1 |
4 |
2 |
|
2 |
1 |
|
|
3 |
1 . |
||||
|
A22 |
2 |
3 |
1 |
|
||
|
|
2 |
2 |
||||
|
|
|
|
|
|
||
Задача 3.
Найти обратную матрицу для матрицы
1 3 5 А 0 1 2 .
0 0 1
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
Вычислим определитель матрицы А разложением по первому столбцу:
46

A |
1 |
1 |
2 |
1 |
0 . |
|
|
0 |
1 |
|
|
|
|
|
|
|
|
Следовательно, обратная матрица для матрицы А существует. Найдем алгебраические дополнения к элементам матрицы А:
A11 |
|
1 |
|
2 |
|
|
1 |
|
A21 |
|
3 |
5 |
|
3 |
A31 |
|
|
3 |
|
5 |
|
11 |
|||||||
|
0 |
|
1 |
|
|
|
|
0 |
1 |
|
|
|
1 |
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
A12 |
|
|
|
2 |
|
0 |
A22 |
|
1 |
5 |
|
1 |
A32 |
|
|
1 |
|
5 |
|
2 |
|||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
0 |
|
1 |
|
|
|
0 |
1 |
|
|
|
|
|
0 |
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
A13 |
|
|
0 |
|
|
0 |
|
A23 |
|
1 |
3 |
|
|
|
0 A33 |
|
1 |
3 |
|
1 |
|
|
|
||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
0 |
|
1 |
|
|
|
|
|
0 |
0 |
|
|
|
|
0 |
1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Значит, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
3 |
11 |
|
1 |
3 |
|
11 |
|
|
|
|
||||||||||
|
|
|
A |
1 |
|
0 |
1 |
|
|
2 |
|
0 |
1 |
|
|
2 . |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
0 |
0 |
|
|
1 |
|
|
0 |
0 |
|
|
1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
3 |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: A 1 0 |
1 |
|
|
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Задача 4.
Найти обратную матрицу для матрицы
2 3 1 А 0 1 1 .
1 1 2
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
|
A |
2 |
|
|
|
1 |
|
1 |
|
3 |
|
|
1 |
|
2 3 |
1 4 |
10 |
0. |
|
|
||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
1 |
2 |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A11 |
|
|
1 |
|
|
3 |
A21 |
|
|
|
3 |
|
|
1 |
|
5 |
A31 |
|
|
|
3 |
1 |
|
4 |
||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1 |
2 |
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
1 |
1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
A12 |
|
1 |
|
1 |
A22 |
|
|
2 |
|
1 |
|
|
|
5 A32 |
|
2 |
|
1 |
|
2 |
||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
1 |
2 |
|
|
|
|
1 |
|
2 |
|
|
|
|
|
0 |
|
1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
A13 |
|
|
1 |
|
|
1 |
|
A23 |
|
2 |
|
|
3 |
|
|
5 |
A33 |
|
2 |
3 |
|
|
2 |
|||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1 |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
0 |
1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
47

|
1 |
3 |
5 |
4 |
0, 3 |
0, 5 |
0, 4 |
|
A 1 |
1 |
5 |
2 |
0, 1 |
0, 5 |
0, 2 . . |
||
|
||||||||
10 |
1 |
5 |
2 |
0, 1 |
0, 5 |
0, 2 |
||
|
|
|||||||
|
0, 3 |
0, 5 |
0, 4 |
Ответ: A 1 |
0, 1 |
0, 5 |
0, 2 . |
|
0, 1 |
0, 5 |
0, 2 |
Задача 5.
При каких x, y, z матрица
1 4 x В 1 5 y 1 6 z
является обратной к матрице
2 2 3 А 1 1 0 ?
1 2 1
Указание
Необходимым условием того, что В = А-1, является требование АВ = Е.
Решение
Проверим невырожденность матрицы А:
A |
3 |
1 |
1 |
1 |
2 |
2 |
3 1 1 ( 4) |
1 0. |
|
1 |
2 |
|
1 |
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Необходимым условием того, что В = А-1, является требование АВ = Е. Найдем АВ:
1 0 2x 2y 3z
AB 0 1 |
x y |
. |
0 0 x 2y z
Для того, чтобы выполнялось условие АВ = Е, x, y, z должны быть решением системы уравнений
2x 2y 3z 0 |
y x |
|
y x |
x |
3 |
|||||
|
|
|
|
4 |
|
|||||
x y 0 |
4x 3z 0 |
z |
|
|
|
x |
y |
3 , |
||
3 |
||||||||||
x 2y z 1 |
x z 1 |
|
|
z |
4 |
|||||
|
|
4 |
|
|
|
|||||
|
|
x |
|
x 1 |
|
|
||||
|
|
3 |
|
|
||||||
|
|
|
|
|
|
|
|
|||
48

1 4 3 В 1 5 3 .
1 6 4
Проверим, будет ли равно единичной матрице произведение ВА:
|
2 |
4 |
3 |
2 |
4 |
6 |
3 |
3 |
1 |
0 |
0 |
|
BA |
2 5 |
3 |
2 5 |
6 |
3 |
3 |
0 |
1 |
0 |
E. |
||
|
2 |
6 |
4 |
2 |
6 |
8 |
3 |
4 |
0 |
0 |
1 |
|
Значит, при найденных значениях x, y, z В = А-1.
Ответ: x = -3, y = -3, z = 4.
1.2. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
1.2.1. Системы с квадратной матрицей. Решение с помощью обратной матрицы.
Правило Крамера
Системы в матричном виде
Система уравнений вида
a11x1 |
a12 x2 |
... |
a1n xn |
b1, |
|
a21x1 |
a22 x2 |
... |
a2n xn |
b2 |
, |
........................................... |
(1) |
||||
|
|||||
am1x1 |
am2 x2 |
... |
amn xn |
bm |
|
называется системой линейных алгебраических уравнений. Числа aij,
i = 1,...,m, j = 1,..., n, называются коэффициентами системы, bi, i = 1,..., m, –
свободными членами, а xj, j = 1,..., n, – неизвестными. Требуется по заданным коэффициентам системы и свободным членам найти решение системы, т.е. все такие числа х1,…, хп, которые удовлетворяют равенствам (4.1). Если таких чисел не существует, то систему называют несовместной, в противном случае (т.е. если существует хотя бы одно решение системы) ее называют
совместной.
Положим
|
a11 |
... |
a1n |
b1 |
x1 |
A |
... |
... |
... , b |
... , x |
... . |
|
am1 |
... |
ann |
bm |
xn |
Матрица А называется матрицей системы, b – столбцом свободных членов, х
– столбцом неизвестных. Из определения умножения матриц вытекает, что равенства (4.1) могут быть записаны в виде
49
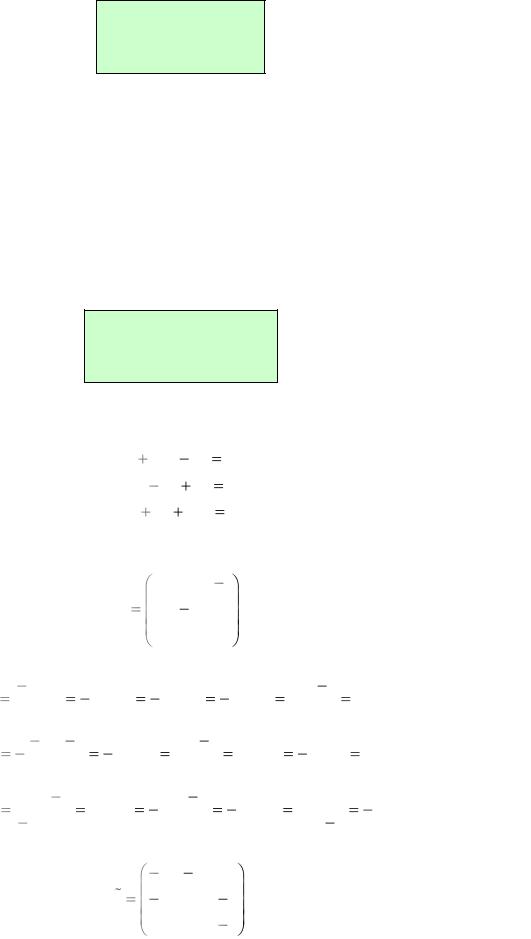
Ax = b, (2)
называемым матричным видом системы.
Решение с помощью обратной матрицы
Пусть дана система линейных алгебраических уравнений в матричном виде (2) с невырожденной квадратной матрицей А. В силу теоремы об обратной матрице (теорема 3.3) у матрицы А существует обратная матрица А-1.
Умножив равенство (4.2) слева на А-1, будем иметь
А-1Ax = A-1b.
Отсюда получаем решение системы
x = A-1b. (3)
Пример 1.
Найти решение системы
x1 2x2 x3 4, 2x1 x2 x3 1, x1 x2 2x3 5
с помощью обратной матрицы. Выпишем матрицу системы
1 2 1 A 2 1 1 .
1 1 2
Найдем присоединенную матрицу Ã. Имеем:
A11 |
1 |
1 |
|
|
3, |
A12 |
2 |
|
1 |
|
|
|
3, |
A13 |
2 |
|
1 |
|
|
3, |
||||
1 |
2 |
|
|
1 |
|
2 |
|
|
|
1 |
|
1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
A21 |
|
1 |
|
5, A22 |
|
1 |
1 |
|
3, |
A23 |
|
|
1 |
2 |
|
|
1, |
|||||||
|
2 |
|
|
|
|
|
|
|
||||||||||||||||
|
1 |
2 |
|
|
1 |
2 |
|
|
|
1 |
1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
A31 |
|
1 |
|
1, |
A32 |
|
1 |
|
1 |
|
|
3, |
A33 |
|
1 |
|
2 |
|
5. |
|||||
2 |
|
|
|
|
|
|
|
|
||||||||||||||||
1 |
1 |
|
|
2 |
|
1 |
|
|
|
2 |
|
1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Следовательно,
|
3 |
5 |
1 |
A |
3 |
3 |
3 . |
|
3 |
1 |
5 |
50

Вычислим определитель матрицы А с помощью разложения по первой строке:
|A| = 1·(-3) + 2·(-3) + (-1)·3 = -12.
Таким образом,
|
1 |
3 |
5 |
1 |
|
A 1 |
3 |
3 |
3 . |
||
12 |
|||||
|
3 |
1 |
5 |
||
|
|
Отсюда
x A 1b |
1 |
|
12 |
||
|
Тем самым х1 = 1, х2 = 2, х3 = 1.
Упражнение 1.
Найти решение системы
x1 x1 x1
с помощью обратной матрицы.
Решение.
3 |
5 |
1 |
4 |
1 |
3 |
3 |
3 |
1 |
2 . |
3 |
1 |
5 |
5 |
1 |
3x2 4x3 6, x2 7x3 7, 2x2 x3 2
1 |
3 |
4 |
6 |
x1 |
A 1 |
1 |
7 , b 7 |
, x x2 . |
|
1 |
2 |
1 |
2 |
x3 |
Вычислим |A| и алгебраические дополнения к элементам матрицы А и найдем обратную матрицу:
|
|
|
|A| |
1 13 1 ( |
5) |
1 ( 17) 9; |
|
|
|
|
|
|
||||||||||||
A11 |
|
7 |
|
13, |
A12 |
|
|
1 |
7 |
|
6, |
A13 |
|
1 |
|
|
1 |
|
|
1, |
||||
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
1 |
|
|
|
1 |
1 |
|
|
1 |
|
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
A21 |
|
4 |
|
5, |
A22 |
|
1 |
4 |
|
|
3, |
A23 |
|
1 |
|
3 |
|
1, |
||||||
3 |
|
|
|
|
|
|
|
|||||||||||||||||
2 |
1 |
|
|
1 |
1 |
|
|
|
|
1 |
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
A31 |
|
3 |
4 |
|
|
17, |
A32 |
|
|
|
1 |
4 |
|
3, A33 |
|
1 |
|
3 |
|
2; |
||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 |
7 |
|
|
|
|
|
1 |
7 |
|
|
|
|
1 |
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
13 |
5 |
|
17 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
A 1 |
6 |
|
3 |
|
3 . |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
9 |
|
|
1 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Воспользуемся формулой (3):
51

|
1 |
13 |
5 |
17 |
6 |
1 |
9 |
1 |
x A 1b |
6 |
3 |
3 7 |
9 |
1 . |
|||
|
9 |
1 |
1 |
2 |
2 |
9 |
9 |
1 |
|
|
|
||||||
Таким образом, х1 = х2 = -1, х3 = 1.
Правило Крамера
Из теоремы об обратной матрице следует, что равенство (4.3) может быть записано в виде
x |A1|Ab.
Следовательно,
(4)
1
xj |A|(b1A1 j ... bn Anj ), j 1,...,n.
Обозначим через j определитель матрицы, которая получается из А заменой j-го столбца на столбец свободных членов:
|
a11 ... |
a1, j |
1 |
b1 |
a1, j |
1 |
... |
a1n |
|
j |
... ... |
... |
|
... |
... |
|
... ... |
. |
|
|
an1 ... |
an. j |
1 |
bn |
an, j |
1 |
... |
ann |
|
Разлагая этот определитель по j-му столбцу, будем иметь:
j = b1A1j + ... + bnAnj.
Тем самым равенства (4) могут быть записаны в виде
(5)
x |
|
1 |
, |
|
|
||||
1 |
|A| |
|||
|
||||
|
... |
|
|
|
x |
|
n |
. |
|
|
|
|||
n |
|A| |
|||
|
||||
Таким образом, доказана
Теорема 4.1 (правило Крамера). Решение системы
Ax = b
с невырожденной квадратной матрицей А единственно и имеет вид (5).
Пример 2.
Найти решение системы
52
