lin2011
.pdf

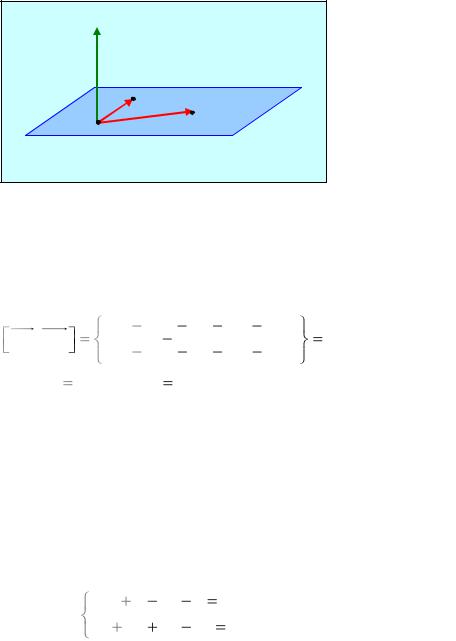
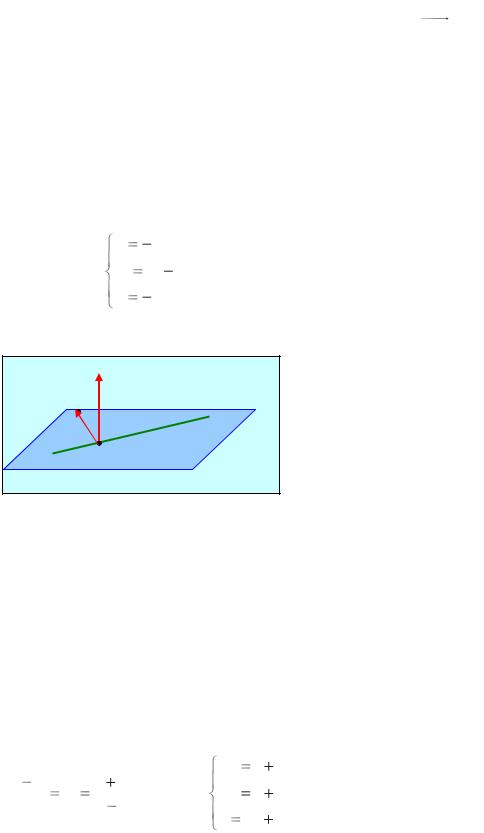
Пусть задана произвольная плоскость Р. Проведем через начало координат прямую, перпендикулярную Р. Точку пересечения ее с плоскостью Р обозначим через R. Через п обозначим единичный вектор, совпадающий с направлением вектора OR (см. рис. 10.4). В случае, если точка R совпадает с О, возьмем в качестве п любой вектор единичной длины.
Так как п – единичный вектор, его координаты имеют вид n (cos , cos , cos ),
где , и - углы между вектором п и осями Ох, Оу и Oz соответственно.
Положим
p |OR|.
Имеем
M {x, y, z} P npOR OM p
|
x cos |
y cos |
z cos |
p. |
Уравнение |
|
|
|
|
|
x cos |
y cos |
z cos |
p 0 |
|
|
|
|
|
называется нормальным уравнением плоскости.
|
z |
|
|
|
R |
|
|
Р |
n |
p |
М |
|
|
||
|
|
|
|
|
O |
|
у |
х |
|
|
|
Рис. 4
Для того чтобы перейти от общего уравнения плоскости
Ax By Cz D 0
к нормальному, надо умножить его на такое число t, для которого
At cos , Bt cos , Ct cos , Dt |
p. |
Так как сумма направляющих косинусов равна единице, то
144