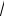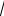lin2011
.pdf




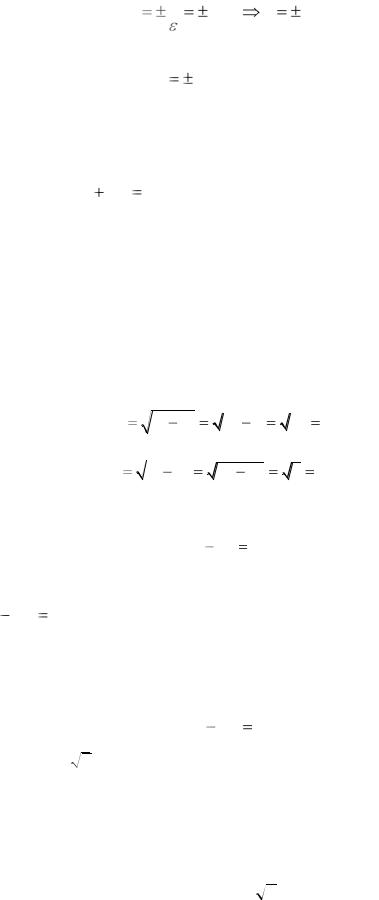

Решение
Найдем координаты нормали к гиперболе в точке М.
Если кривая задана уравнением F(x,y) = 0, то нормаль к ней в точке М0={х0;у0}
имеет координаты: п = (F′x(x0;y0);F′y(x0;y0)).
|
2x , |
|
|
|
2y |
|
|
y |
|
|
|
|
|
|
|
2 15 |
10 , |
|||
F |
F |
|
|
, |
F (15; |
4 6) |
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
x |
9 |
y |
4 |
2 |
|
x |
|
|
|
9 |
3 |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
4 6 |
|
|
|
|
|
|
|
|
10 ; 2 |
|
|
|
||
|
F (15; |
4 |
6) |
|
2 6 |
|
n |
6 . |
||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
y |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Уравнение прямой, проходящей через точку М0(х0;у0)
перпендикулярно вектору п = {A, B}, имеет вид: А(х – х0) + В(у – у0) = 0.
Запишем уравнение касательной:
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(x |
15) |
2 |
6(y 4 |
6) |
0, |
||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
10 x 50 |
|
|
|
|
|
|
|
|
|
|
|||
2 |
6y |
48 |
0, 5x |
3 |
6y 3 0. |
||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: Уравнение касательной:
5x 3
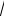 6y 3 0.
6y 3 0.
Задача 11.
Составить уравнение параболы, если даны ее фокус F(2; -1) и директриса
х – у – 1 = 0.
Указание
Используйте определение параболы: параболой называется геометрическое место точек, для каждой из которых расстояние до фокуса равно расстоянию до директрисы.
Решение
Используем определение параболы:
Параболой называется геометрическое место точек, для каждой из которых расстояние до фокуса равно расстоянию до директрисы.
Пусть точка М(х, у) лежит на параболе. Тогда ее расстояние до фокуса
MF 
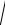 (x 2)2 (y 1)2 .
(x 2)2 (y 1)2 .
199



 13 3
13 3
 13
13
 13
13 
 13
13
 3,
3, 
 6
6