4.9. Литература

1. Кориков, А. М. Основы теории управления : учеб. пособие / А. М. Кориков. – Томск : Томск. межвуз. центр, 2001.

2. Ануфриев, И. Е. Самоучитель Matlab 5.3/6.x / И. Е. Ануфриев. – СПб. : БХВ-Петербург, 2002.

3. Мартынов, Н. Н. Введение в Matlab 6 / Н. Н. Мартынов. – М. : КУДИЦ, 2002.

4. Семенов, В. В. Математическая теория управления в примерах и задачах / В. В. Семенов, А. В. Пантелеев, А. С. Бортаковский. – М. : МАИ, 1997.

5. Методы классической и современной теории автоматического управления : учебник : в 3 т. / под общ. ред. Н. Д. Егупова. – М. : Изд-во МГТУ им. Н. Э. Баумана, 2000.

6. Юревич, Е. И. Теория автоматического управления / Е. И. Юревич. – Л. : Энергия, 1969.

Лабораторная работа № 5

Исследование устойчивости

линейных динамических моделей

с использованием ППП Control System Toolbox

системы MatLab 6.x

Содержание

5.1. Общие указания к выполнению лабораторной работы.

5.2. Цель работы.

5.3. Постановка задачи.

5.4. Краткие сведения из теории.

5.5. Методика выполнения работы.

5.6. Задание к лабораторной работе.

5.7. Методический пример.

5.8. Отчет по лабораторной работе.

5.9. Варианты заданий.

5.10. Контрольные вопросы.

5.11. Литература.

 

5.1. Общие указания к выполнению лабораторной работы

Лабораторная работа выполняется на персональном компьютере в операционной среде Windows с установленной системой MatLab 6.х и пакетом прикладных программ Control System Toolbox 5.

5.2. Цель работы

Исследование устойчивости и качества систем автоматического управления с помощью временных (динамических) и частотных характеристик. Данное исследование проводится с использованием пакета прикладных программ Control System Toolbox системы инженерных расчетов MatLab 6.

5.3. Постановка задачи

В качестве объекта исследования в лабораторной работе выступают линейные (линеаризованные) динамические стационарные системы управления с одним входом и одним выходом. При этом модель одномерной САУ задана в виде комплексной передаточной функции, записанной как отношение полиномов:

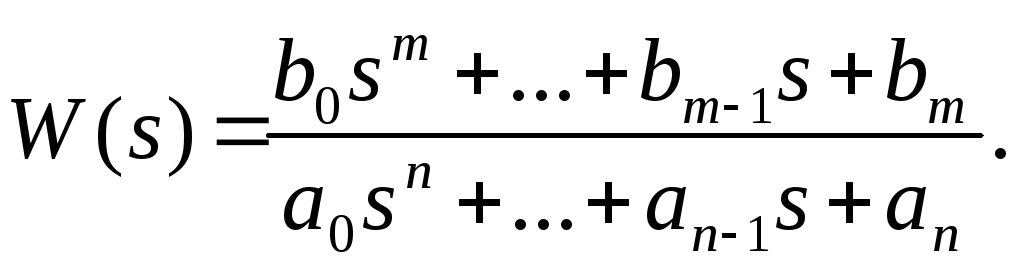
Требуется:

1. Определить полюса и нули передаточной функции

2. Записать дифференциальное уравнение, определяющее функционирование САУ.

3. Построить графики переходной и импульсно-переходной функции: h(t), w(t).

4. Построить логарифмические частотные характеристики L (ω).

5. Построить частотный годограф Найквиста W(jω ), ω = [0, ∞].

5.4. Краткие сведения из теории

Система автоматического управления (САУ) описывается линейным (линеаризованным) дифференциальным уравнением вида:

5.1.

где x(t) – входной процесс;

y(t) – выходной процесс;

a_i, b_j, – постоянные коэффициенты;

n, m (n ≥ m) – постоянные числа.

В операторной форме выражение (5. 1) может быть записано так:

А(s) у(s) = В(s) х(s).

Здесь s – оператор дифференцирования

Отсюда преобразование «вход-выход» системы:

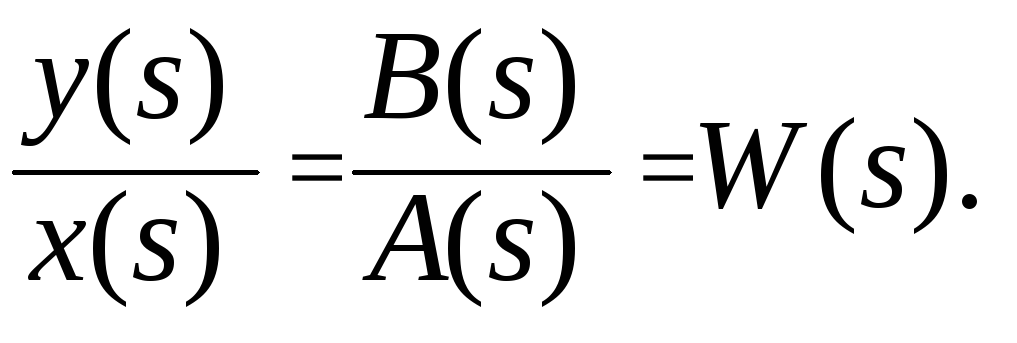
(5.2)

W(s) называется операторной передаточной функцией.

Один из способов моделирования систем заключается в представлении преобразования «вход-выход» в виде комплексной передаточной функции:

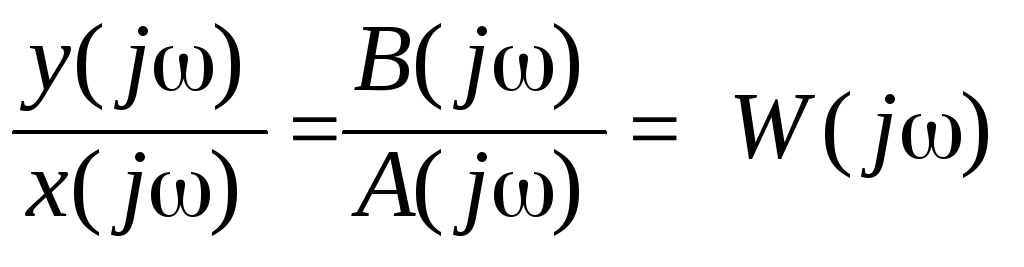, (5.3)

которая получается путем применения преобразования Лапласа к (5.2) при начальных нулевых условиях. Здесь s – комплексная переменная, s = jω. Связь между операторной (5.2) и комплексной (5.3) передаточными функциями можно записать в виде:

Комплексные числа, являющиеся корнями многочлена В(s), называются нулями передаточной функции, а корни многочлена A(s) – полюсами.

Динамические свойства систем характеризуются при помощи реакции системы на входные воздействия специального вида, в частности выход системы на единичный скачок и импульсную δ-функцию (дельта-функцию).

Пусть x(t) = 1(t), т.е. на вход системы подается функция Хевисайда (единичный скачок), определяемая

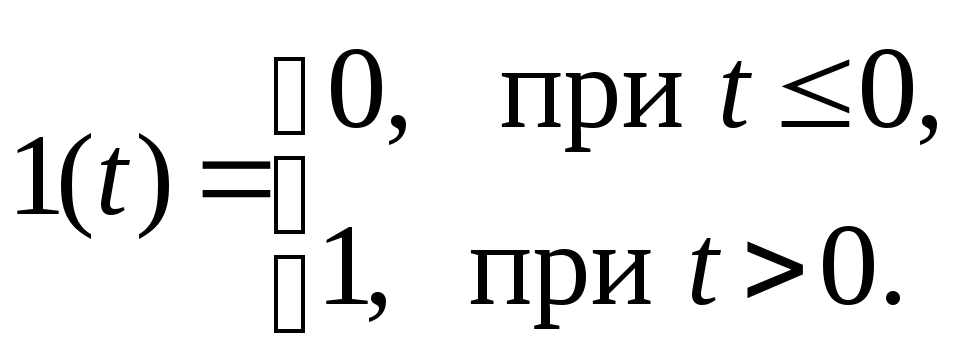
График функции Хевисайда приведен на рис. 5.1.

Реакция САУ на единичный скачок называется переходной функцией системы и обозначается h(t).

Рис. 5.1. Функция Хевисайда

Если x(t) = δ(t), т.е. на вход системы поступает функция Дирака (δ-функция, импульсная функция) (рис. 5.2), определяемая

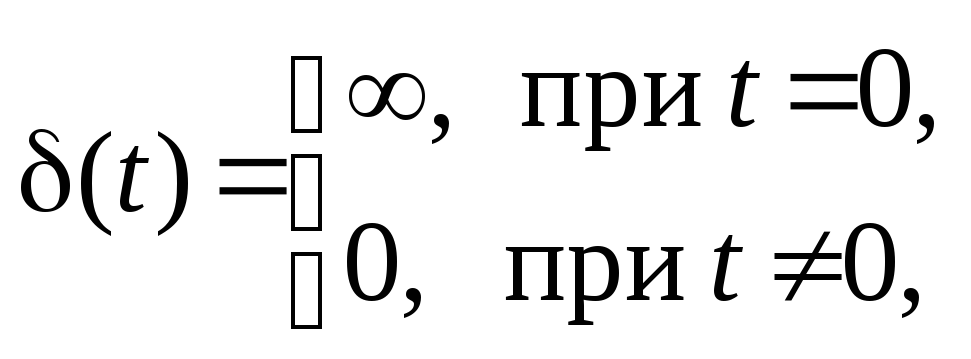
то реакция САУ называется импульсной переходной функцией системы и обозначается w(t).

Рис. 5.2. Функция Дирака

Импульсная и переходная функции системы связаны соотношением:

Благодаря широкому применению при исследовании устойчивости динамических систем и проектировании СУ, получили распространение частотные характеристики.

Пусть на вход системы с передаточной функцией W(s) подается гармонический сигнал

x(t) = a_x cos (ωt), t > 0.

В этих условиях справедлива следующая теорема. Если звено является устойчивым, то установившаяся реакция y(t) на гармоническое воздействие является функцией той же частоты с амплитудой

a_y = a_x |W(jδ)|.

и относительным сдвигом по фазе

φ = arg W(jδ).

Таким образом:

y(t) = a_x |W(jω)| cos (ω t + arg W(jω)),

где j – комплексная единица;

–частотная характеристика.

Частотной характеристикой W(jω) стационарной динамической системы называется преобразование Фурье переходной функции:

где w(t – τ ) – импульсная переходная функция.

Связь между комплексной передаточной функцией и частотной характеристикой определяется соотношением:

.

При фиксированном значении ω частотная характеристика является комплексным числом и, следовательно, может быть представлена в виде:

.

Здесь

– амплитудно-частотная характеристика (АЧХ);

–фазово-частотная характеристика (ФЧХ);

–вещественная частотная характеристика (ВЧХ);

– мнимая частотная характеристика (МЧХ).

Геометрическое место точек W(jω) на комплексной плоскости при изменении ω от ω₀ до ω₁ (обычно ω₀ = 0, ω₁ = ∞), называется амплитудно-фазовой характеристикой (АФХ) или частотным годографом Найквиста.

Имеет широкое практическое значение диаграмма Боде (логарифмическая амплитудная частотная характеристика ЛАЧХ), которая определяется как L = 20 lg A(ω) измеряется в децибелах и строится как функция от lg ω.