Непрерывно распределенные двумерные случайные величины

Если функция распределения F(x, y) непрерывна и существует такая неотрицательная интегрируемая функция р(x, y), что выполняется равенство

, (6.1)

то двумерная с.в. (Х, Y ) называется непрерывно распределенной двумерной с.в. (или непрерывной двумерной с.в.). Функция р(x, y) называется плотностью распределения двумерной с.в. (Х, Y ).

Равенство (6.1) позволяет по плотности распределения найти функцию распределения. Следовательно, закон распределения двумерной с.в. может быть задан как при помощи функции распределения, так и при помощи плотности распределения.

Плотность распределения непрерывной двумерной с.в.

Свойства плотности распределения.

1. р(x, y) ³ 0;

1. свойство нормировки ;

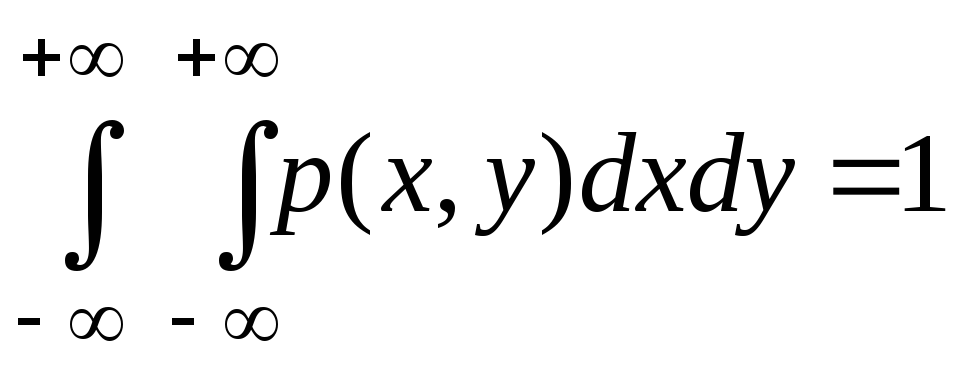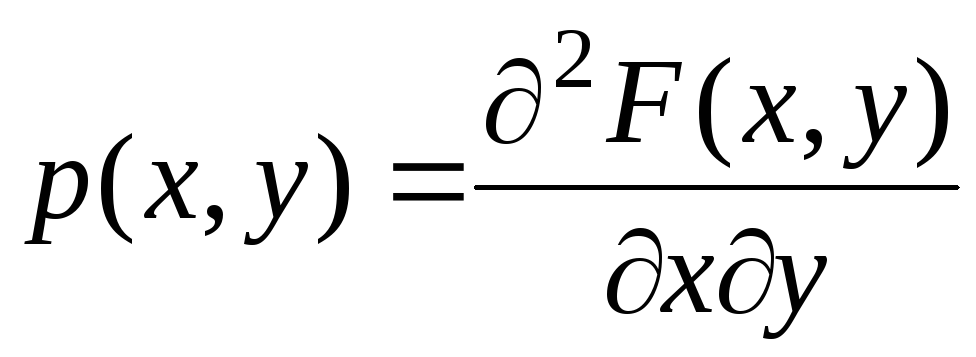2. , если р(x, y) непрерывна в точке (x, y);

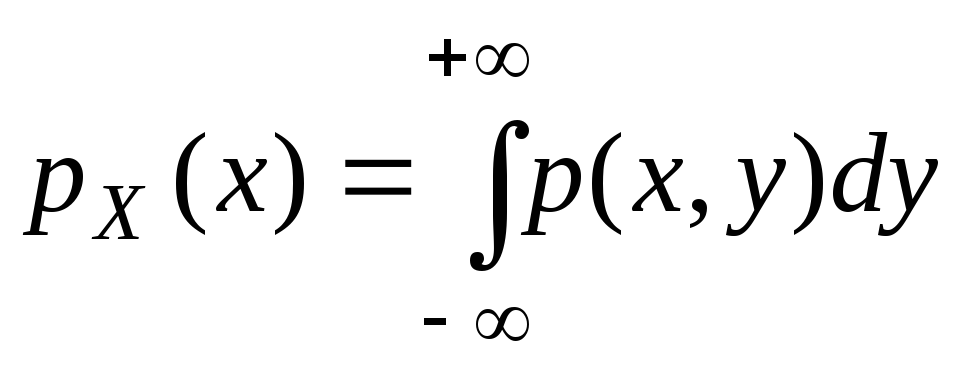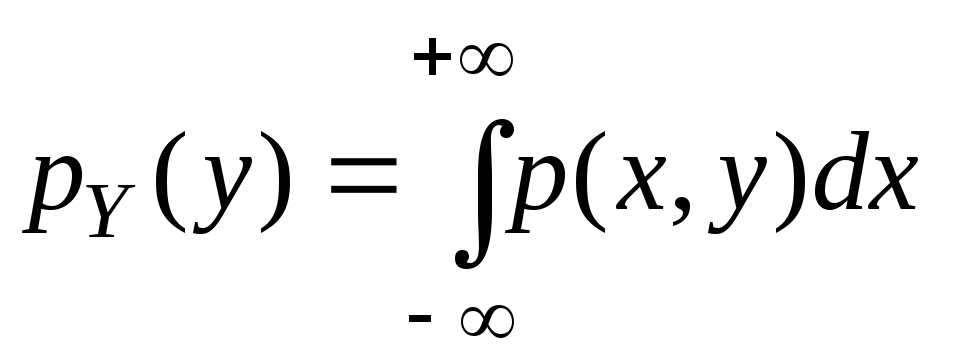3. , , где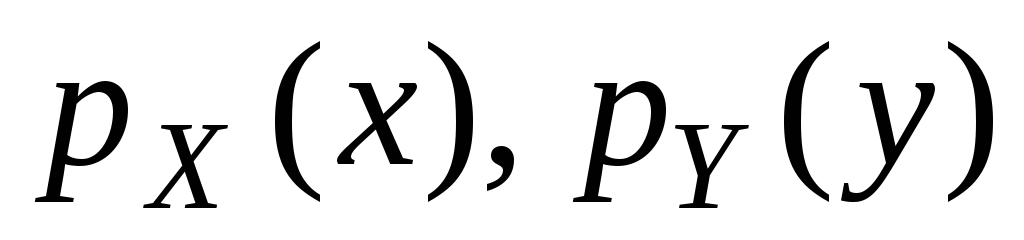– плотности одномерных с.в.Х и Y соответственно;

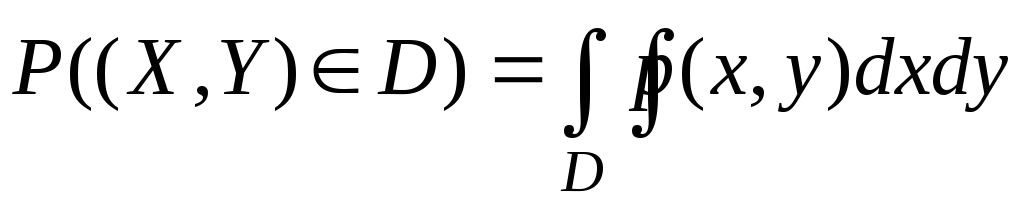4. , где D – множество на плоскости, имеющая площадь.

Формула 5 означает, что вероятность попадания двумерной с.в. в область D равна двойному интегралу от плотности.

Первое свойство следует из определения плотности распределения.

Свойство нормировки следует из того, что

.

Третье свойство следует из формулы (6.1) по правилу дифференцирования интеграла по верхнему пределу интегрирования.

Четвертое свойство следует из следующей цепочки равеннств:

.

Пятое свойство примем без доказательства.

6.2 Независимость двух случайных величин.

Случайные величины Х, Y называются независимыми, если

для всех x, y.

Из этого равенства следует, что непрерывные с.в. Х, Y являются независимыми в том и только в том случае, когда для всехx, y.

Две дискретные случайные величины Х, Y являются независимыми в том и только в том случае, когда для всехi, j.

Условные плотности распределения.

Пусть в результате опыта с.в. Y приняла конкретное значение y и . Тогдаусловной плотностью распределения вероятностей с.в. Х при условии Y=y называется функция от переменной х:

.

Аналогично определяется условная плотность распределения вероятностей с.в. Y при условии Х =х:

().

Из определений условной плотности распределения вероятностей и независимости с.в. следует, что если с.в. Х, Y независимы, то условные плотности распределения вероятностей совпадают с соответствующими плотностями одномерных с.в.: .

Замечание 6.1 Подобно двумерной случайной величине в теории вероятностей вводится многомерная с.в. и связанные с ней понятия функции и плотности распределения, независимости нескольких с.в. и т.д.

6.3 Корреляционный момент, коэффициент корреляции

Корреляционным моментом (или ковариацией) называется величина

,

где m_x =M[X], m_y=M[Y] – математические ожидания с.в. Х, Y соответственно.

Корреляционный момент характеризует степень влияния одной случайной величины на другую: чем он больше, тем больше это влияние.

Случайные величины Х, Y называются некоррелированными, если K_X,Y=0.

Теорема 6.1 D(X+Y) = D(X) + D(Y) + 2K_X,Y.

В самом деле, =

==+=

= D(X) + D(Y) + 2K_X,Y.

Свойства корреляционного момента.

1. .

2. .

3. .

Доказательства свойств.

1. =

=.

2. .

3. Из неотрицательности дисперсии для любого действительного значения t имеем . По теореме 6.1 имеемD(X) + 2 tK_X,Y.+ t²D(Y).

Квадратный трехчлен D(X) + 2 tK_X,Y.+ t²D(Y) ³ 0 при любом действительном t, если его дискриминант неотрицателен: . Откуда следует

Þ.

Свойства некоррелированных с.в.

1. Если Х, Y независимы, то они некоррелированны.

2. Если Х, Y некоррелированны, то М[XY] = M[X] M[Y].

3. Если Х, Y некоррелированны, то D(X+Y) = D(X) + D(Y).

Доказательство. 1. Если Х, Y независимы, то М[XY] = M[X] M[Y] (по свойству 4 м.о.). Тогда по свойству 1 корреляционного момента =0.

2. Если Х, Y некоррелированные, то по свойству 1 корреляционного момента получаем =0Þ M[X] M[Y].

3. Так как 0, то из теоремы 6.1 следуетD(X+Y) = D(X) + D(Y).

Замечание 6.2 Из свойства 1 следует, что из независимости двух с.в. следует их некоррелированность. Оказывается, что обратное утверждение неверно [ ]. Таким образом, независимость двух с.в. более сильное свойство, чем некоррелированность.

Замечание 6.3 Как известно, свойства

М[XY] = M[X] M[Y] и D(X+Y) = D(X) + D(Y)

верны для независимых с.в. (см. пп. 4.3 и 4.4). Как следует из свойств некоррелированных с.в., эти свойства верны и для некоррелированных с.в., т.е. при более слабых требованиях.

Коэффициентом корреляции называется величина

.

Свойства коэффициента корреляции.

1. .

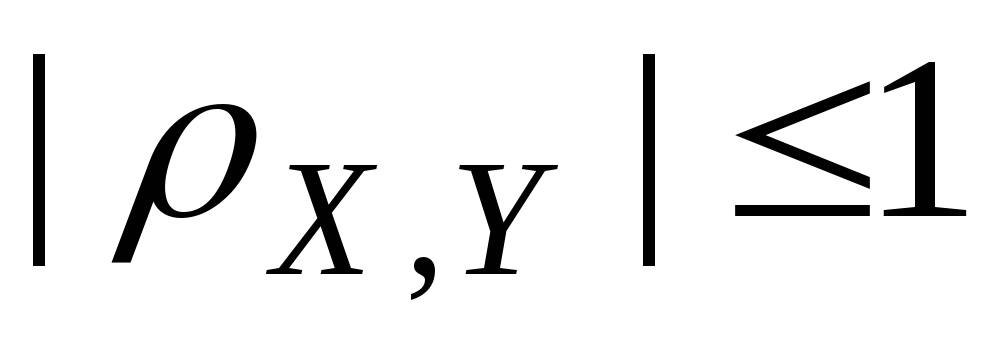2. Х, Y некоррелированны Û .

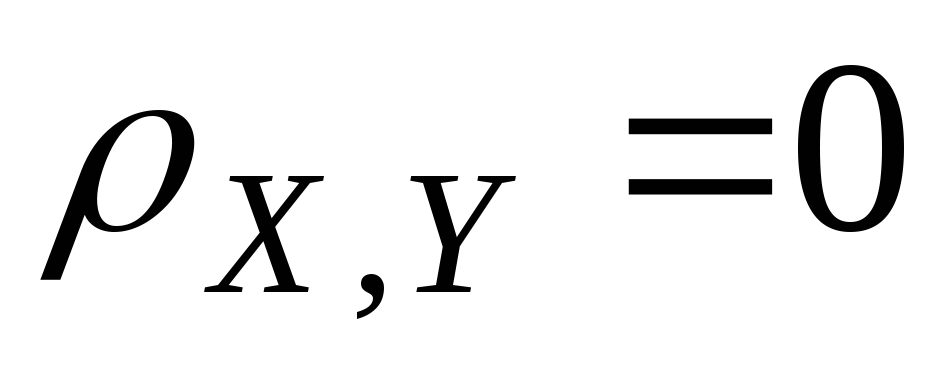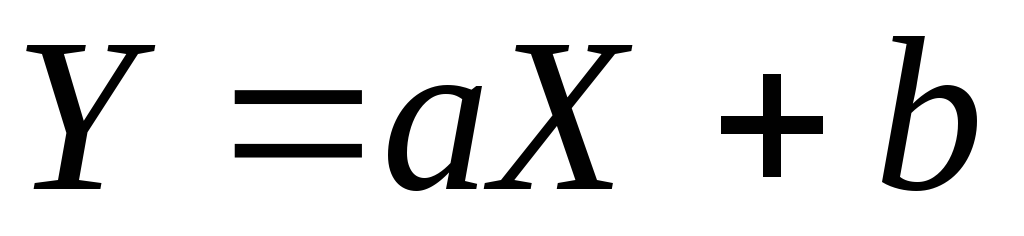3. (a, b – константы) Þ .

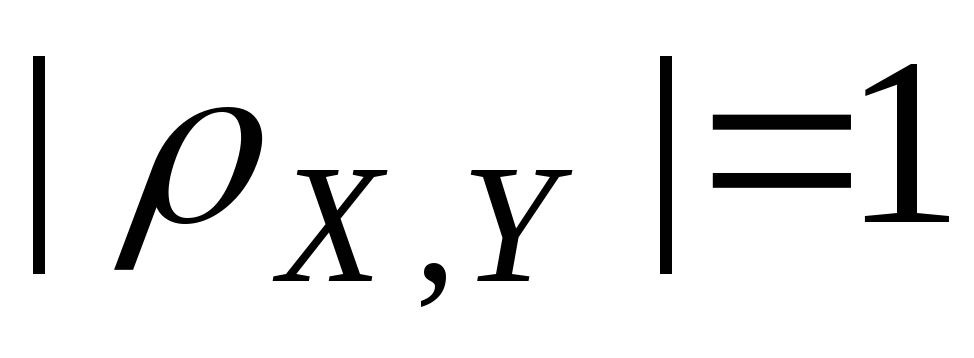Доказательство 1. Если разделить обе части неравенства из свойства 3 корреляционного момента на , то получим.

2. Сразу следует из определений.

3. Если , то=

=.

.

.

Как упоминалось выше, корреляционный момент характеризует степень влияния одной случайной величины на другую. Однако, с помощью него нельзя оценить степень коррелированности различных пар с.в. Например, если Х, Y измерить в сантиметрах, а затем перевести их значения в миллиметры, то соответственно корреляционный момент изменит свою числовую величину, хотя от этого степень влияния их друг на друга не изменится. Очевидно, коэффициент корреляции при этом не изменит своего значения. Таким образом, при помощи коэффициента корреляции можно сравнивать степень коррелированности любых пар случайных величин. Более того, коэффициент корреляции показывает степень линейной связи между двумя случайными величинами: если , то одна выражается линейно через другую; еслиблизко к 1, то между ними есть почти линейная связь.