
- •Теория вероятностей и математическая статистика
- •1.2 События и действия (операции) над ними.
- •1.3 Классическое определение вероятности
- •1.4. Свойства вероятностей
- •1.5. Формула сложения вероятностей
- •Эта формула называется формулой сложения вероятностей для несовместных событий и читается так: вероятность суммы нескольких попарно несовместных событий равна сумме их вероятностей.
- •1.6. Статистическое и геометрическое определения вероятности
- •Геометрическое определение вероятности.Вероятностью событияА называется.
- •1.7. Понятие об аксиоматическом определении вероятности.
- •2.1 Условная вероятность
- •2.2 Формула умножения вероятностей.
- •2.3 Формула полной вероятности
- •2.4 Формула Байеса
- •2.5 Схема и формула Бернулли
- •2.5 Приближенные формулы в схеме Бернулли
- •Лекция 3
- •3.1 Случайная величина
- •3.2 Дискретные случайные величины
- •3.4 Непрерывные случайные величины
- •Свойства плотности вероятности.
- •Смысл дисперсии в том, что она является мерой рассеяния значений случайной величины от математического ожидания. Чем меньше дисперсия, тем меньше разброс значений от математического ожидания.
- •4.4 Свойства дисперсии
- •4.5 Другие числовые характеристики
- •4.6 Нормальное распределение (распределение Гаусса)
- •Лекция 5
- •5.1 Числовые характеристики некоторых распределений
- •Равномерное распределение.
- •Непрерывно распределенные двумерные случайные величины
- •6.3 Корреляционный момент, коэффициент корреляции
- •6.4 Представление о законе больших чисел
- •6.5 Представление о центральной предельной теореме
- •Лекция 7
- •Рассмотрим три закона распределения, которые часто используются в теории вероятностей.
- •1. Распределение (читается “хи в квадрате”). ПустьÎn(0, 1) – независимые нормально распределенные с.В. С.В. Называетсяраспределенной по закону со степенью свободыk.
- •2. Распределение Стьюдента т(k). С.В. , гдеU în(0, 1), называется распределенной по закону Стьюдента со степенью свободы k.
- •3. С.В. , гдеk1, k2 – натуральные числа, называется распределенной по закону Фишера со степенями свободы k1, k2.
- •7.4.1 Доверительный интервал для м.О. Нормально распределенной с.В.
- •7.4.2 Доверительный интервал для дисперсии нормально распределенной г.С.
- •8.1 Предварительная обработка реализации выборки
- •F*(X) – статистическая функция распределенияр(X) – плотность распределения
- •8.2 Основные понятия проверки статистических гипотез
- •Лекция 9. Элементы регрессионного анализа
- •9.1 Парный линейный регрессионный анализ.
- •9.2 Парный обобщенный линейный регрессионный анализ
4.4 Свойства дисперсии
1.
![]() .
.
2.
![]() .
.
3
![]() ,C=const.
,C=const.
4.
![]() ,
C=const.
,
C=const.
5. D(X+Y)=D (X)+D(Y), если с.в. X,Y независимы.
В частности, D(X+C)=D(X), C=const;
Докажем равенство 1.
![]()
=![]() .
.
Использованы свойства м.о. и тот факт, что M [X] = const.
Доказательство 5. По свойству 1 имеем D(X+Y)=M[(X+Y)2]– (M[X]+ M[Y])2=
![]()
=![]()
По свойству 4 м.о.
![]() .
.
=![]() .
.
4.5 Другие числовые характеристики
Начальным моментом k-го порядка случайной величины X называется математическое ожидание случайной величины Xk
![]() .
.
Заметим n1=M[X].
Центральным
моментом k-го
порядка называется
![]() .
.
Заметим, что
![]() .
.
Медиана – это такое число Ме(Х), что F(Ме(Х))=0,5.
Мода – точка максимума плотности распределения. Если у с.в. одна мода, то распределение называется унимодальным.
Квантилью порядка a (0<a<1) называется такое число xa, что F(xa)= a. Заметим, что квантиль порядка 0,5 совпадает с медианой.
Коэффициентом
асимметрии называется
число
![]() .
.
Коэффициентом
эксцесса называется
число
![]() .
.
4.6 Нормальное распределение (распределение Гаусса)
Случайная величина Х называется нормально распределенной (имеющей распределение Гаусса), если ее плотность вероятности имеет вид
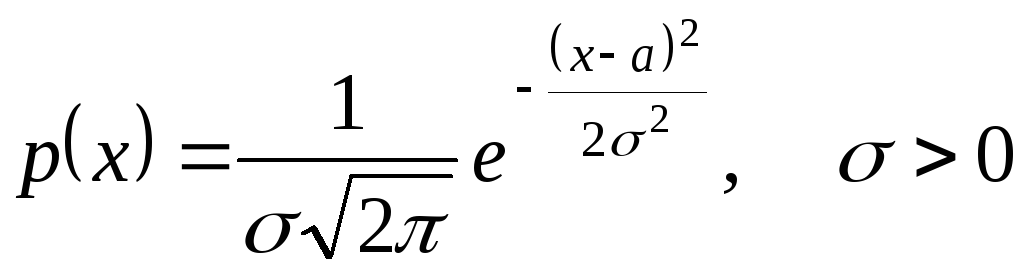 .
.
Нормальное распределение будем обозначать N(a,s). Тогда XÎN(a,s) означает, что с.в. X имеет нормальное распределение с параметрами a,s. Плотность зависит от двух параметров a и s > 0, смысл которых выясним в дальнейшем.
Функция распределения равна
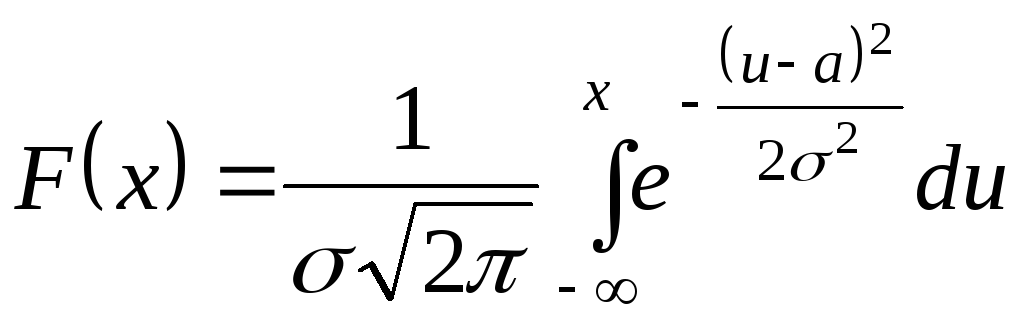 .
.
Докажем, что плотность распределения удовлетворяет свойству 4 нормировки плотности распределения (лекция 3).
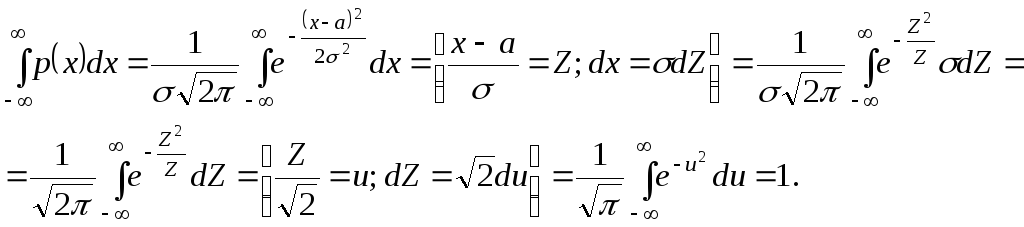
График плотности нормального распределения см. на рисунке 4.1.
Рисунок
4.5
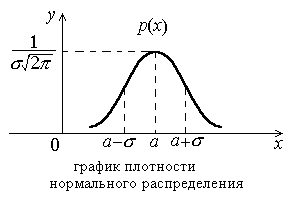
Если параметры a = 0, σ = 1, то такая нормально распределенная случайная величина называется стандартной нормальной случайной величиной.
В природе часто встречаются нормально распределенные с.в. Так, «естест-венные» размеры человека (рост, вес и т.д.), деревьев (высота, диаметр ствола) распределены нормально. Причина этого явления раскрывается в теореме Ляпунова, о которой речь пойдет в дальнейшем.
Лекция 5
5.1 Числовые характеристики некоторых распределений
Биномиальное
распределение.
Это распределение рассматривалось в
примере 3.2 (лекция 3). Пусть Х
– распределена
по биномиальному закону с параметрами
n,
p
(n
– число испытаний, p
–вероятность успеха), q=1–p.
Рассмотрим с.в. Хi
c
законом распределения 0®q,
1®p
(i
= 1,2, …, n).
Математическое ожидание
![]() .
Случайная величина
.
Случайная величина![]() ,
причем с.в.
,
причем с.в.![]() независимы и распределены одинаково.
Следовательно,
независимы и распределены одинаково.
Следовательно,
![]() .
.
Вычислим дисперсию
![]() .
.
![]() .
.
Итак,
-
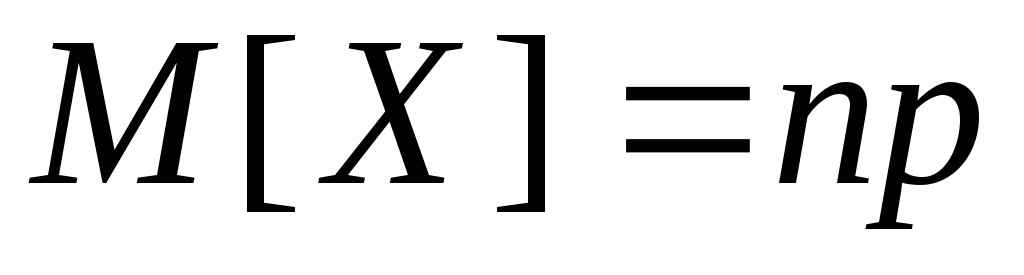 .
.
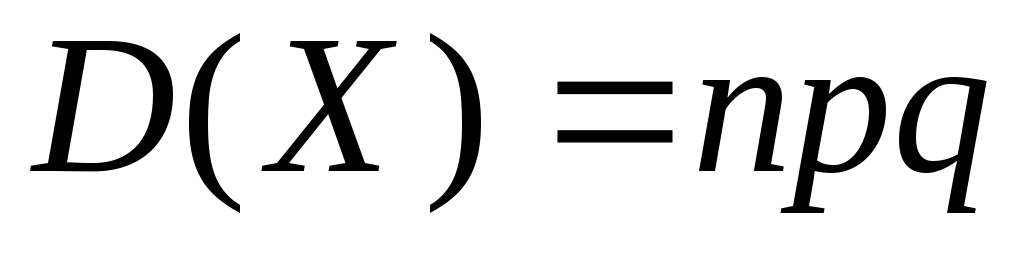
Распределение Пуассона. Пуассоновскийзакон распределение
имеет вид
![]() ,xi
= i
= 0, 1, … .
,xi
= i
= 0, 1, … .
![]() .
.
![]()
=![]() =
=
=![]() .
.
Итак,
-
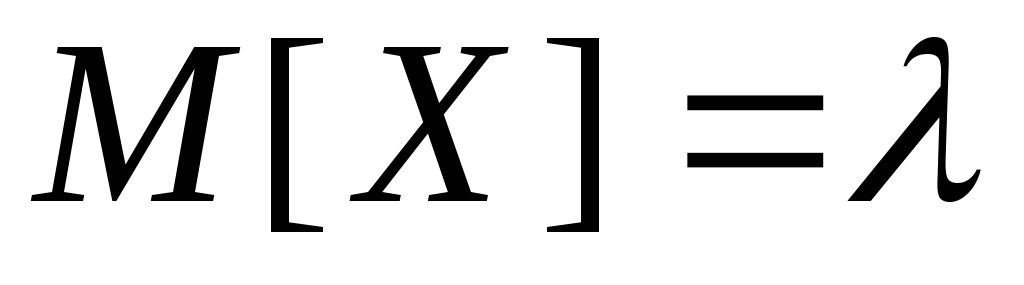 .
.
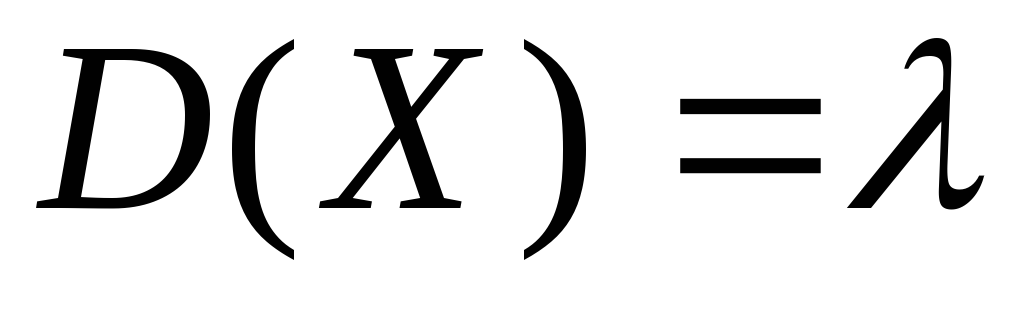 .
.
Равномерное распределение.
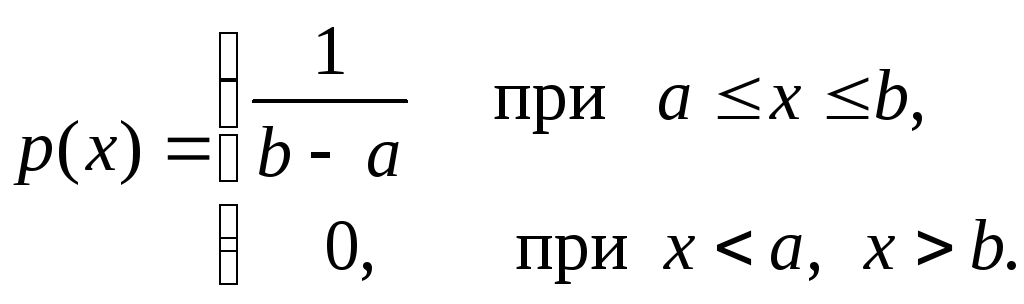
![]() .
.
![]() .
.
Итак,
-
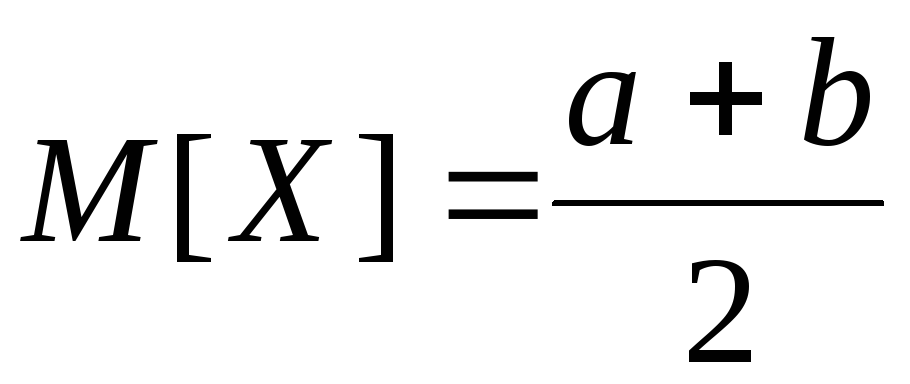 .
.
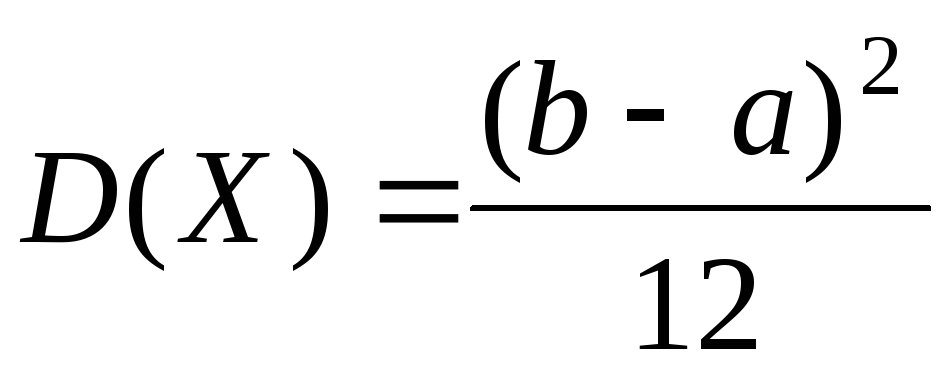 .
.
Показательное распределение.
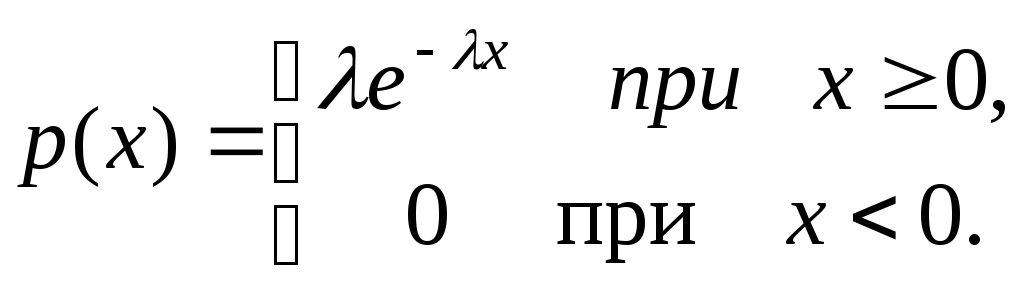
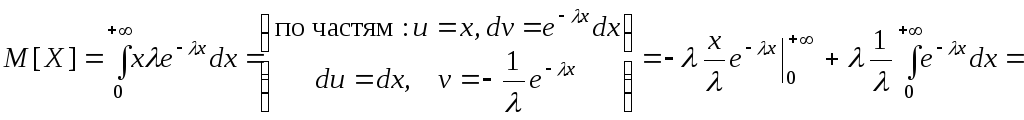
=![]() .
.
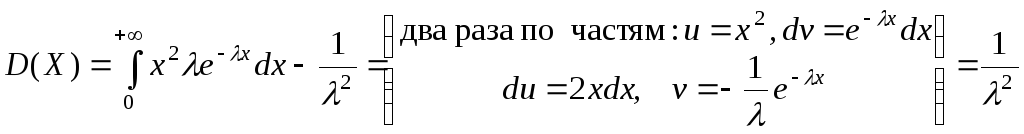 .
.
Итак,
-
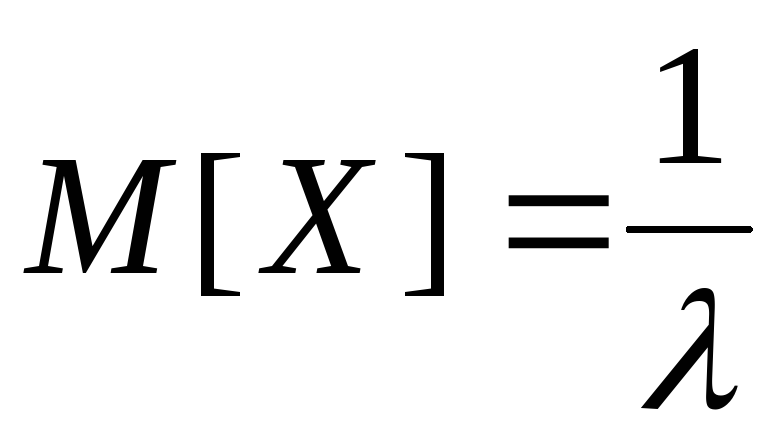 .
.
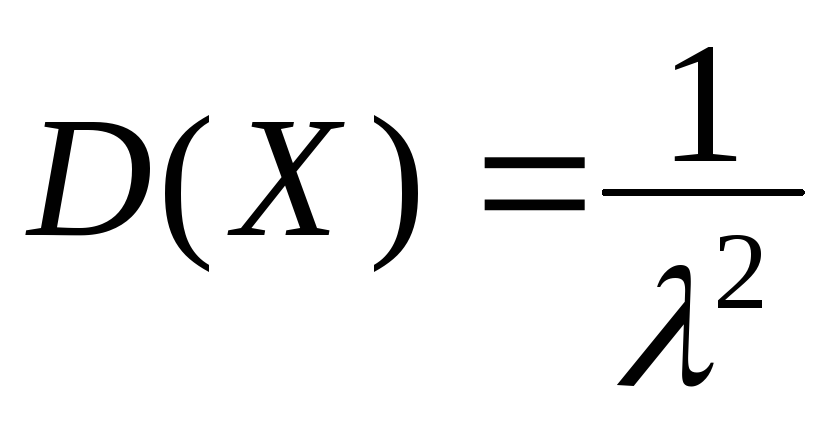 .
.
Нормальное распределение.
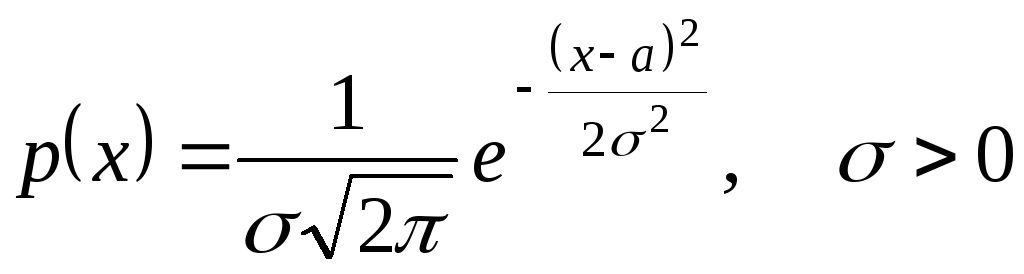
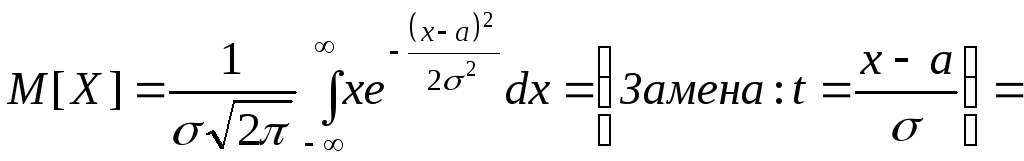
 .
.
Аналогично можно
вычислить дисперсию ![]() .
.
Итак,
-
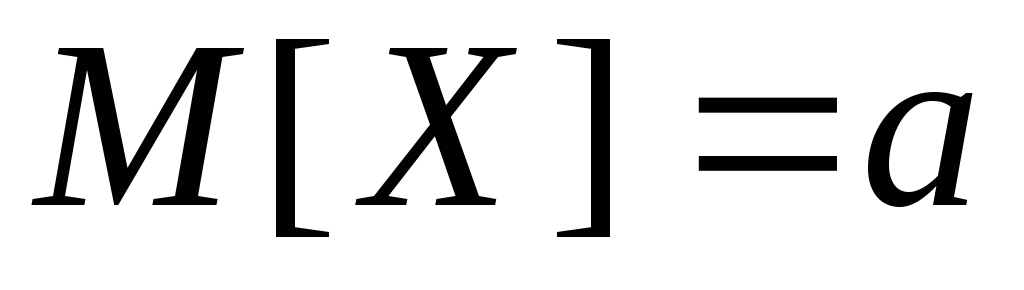 .
.
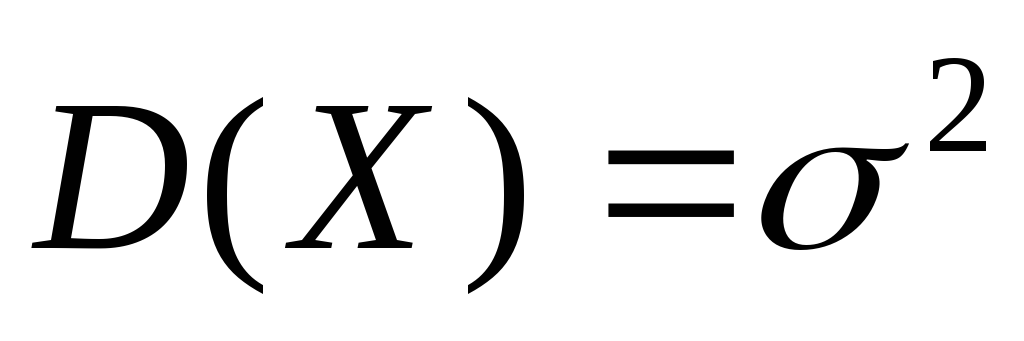 .
.
5.2 Вероятность попадания с.в. в числовой промежуток
Пусть Х
– ДСВ. Тогда
![]() .
.
Рассмотрим НСВ Х.
Так как ![]() для любого числа с,
то для НСВ вероятности
для любого числа с,
то для НСВ вероятности ![]() =
=![]() =
=![]() =
=![]() .
.
Для вычисления
вероятности ![]() можно применить две
формулы:
можно применить две
формулы:
![]() ,
,
![]() .
.
Если интеграл
“берущийся”, то никаких проблем не
возникает. Для нормального распределения
вопрос вычисления вероятности ![]() стоит особо, так как
интеграл получается не “берущийся” и
на практике часто приходится вычислять
эту вероятность.
стоит особо, так как
интеграл получается не “берущийся” и
на практике часто приходится вычислять
эту вероятность.
Предварительно
рассмотрим функцию Лапласа, вычислению
которой приводится задача вычисления
вероятности ![]() для нормального
распределения.
для нормального
распределения.
Функцией Лапласа называется функция
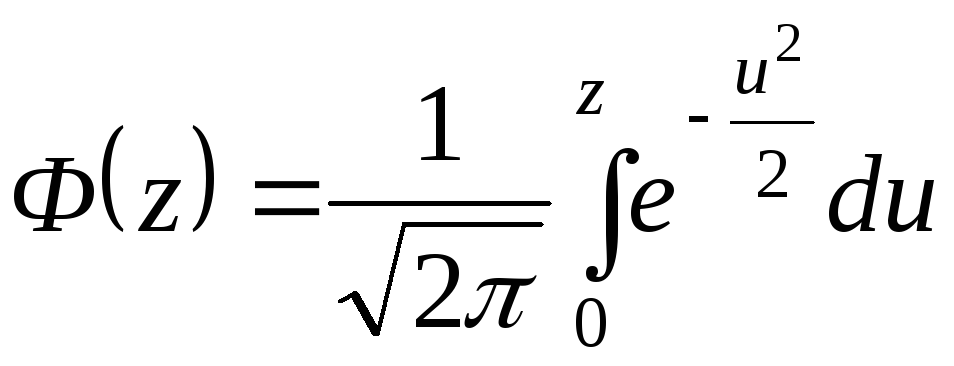 .
.
Свойства функции Лапласа.
1) при z>0 функция Лапласа определяет вероятность попадания стандартной нормальной случайной величины в интервал (0, z).
2)
![]() .
.
3)
![]() – функция нечетная.
– функция нечетная.
4)
![]() для значенийz
³
5.
для значенийz
³
5.
Иногда в литературе встречаются другой вид функции Лапласа:
![]() .
.
Функция Лапласа табулирована (см. [ ]).
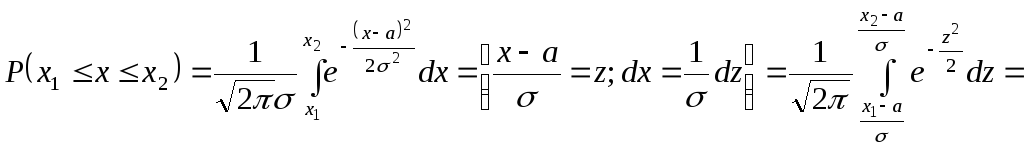
=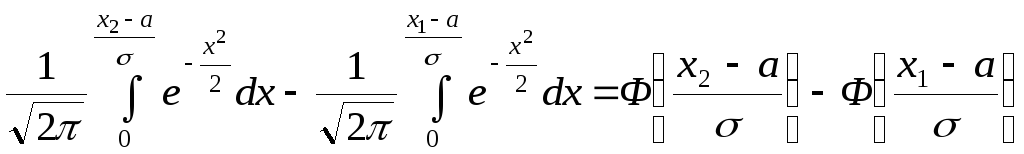
![]()
Таким
образом, если с.в. Х
распределена
нормально с параметрами M[X]=a
и
![]() ,
то верна формула
,
то верна формула
![]() .
.
Лекция 6
6.1 Двумерная и многомерная случайная величина
Пусть (W,U, P) – некоторое вероятностное пространство, Х, Y – две случайные величины, определенные в этом пространстве. Пара (Х, Y ) называется двумерной случайной величиной (или двумерным случайным вектором).
Закон распределения двумерной случайной величины может быть задан при помощи двумерной функции распределения.
Функцией распределения
двумерной с.в.
называется двумерная действительная
функция
![]() .
.
Событие
![]() означает сокращенную запись события
означает сокращенную запись события![]() .
.
Аналогично доказательствам свойств одномерных функций распределений можно доказать следующие свойства двумерных функций распределений.
Обозначим
![]() одномерные функции распределения с.в.Х,
Y соответственно.
одномерные функции распределения с.в.Х,
Y соответственно.
Свойства двумерных функций распределений.
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4) F(x, y) не убывает по каждой переменной;
5) F(x, y) непрерывна слева по каждой переменной;
6)
![]() .
.
Дискретные двумерные случайные величины.
Пусть Х, Y – две дискретные случайные величины, имеющие следующие законы распределения соответственно:
pi·=
P(X
=
xi)
(x1<x2<
…), p·
j
=
P(Y=
yj)
(y1<y2<
…),
![]() .
.
Двумерная с.в. (Х, Y ) называется дискретной двумерной случайной величиной (или дискретно распределенной двумерной случайной величиной).
Закон распределения
двумерной дискретной с.в. может быть
задан в виде функции
![]()
![]() ,
где
,
где![]() .
.
Если с.в. Х принимает конечное множество значений x1, x2, …, xn , а Y – конечное множество значений y1, y2, …,ym , то закон распределения задают обычно в виде таблицы 6.1. В этой таблице
![]()
![]() ,
,
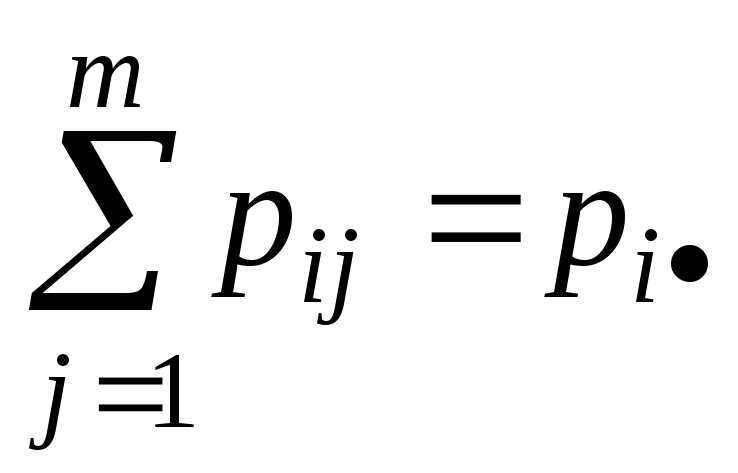
![]() .
.
Заметим, что первая и последняя строки таблицы 6.1 задают закон распределения с.в. Y, а первый и последний столбцы – закон распределения с.в. Х.
Таблица 6.1
-
y1
y2
×××
ym
å
x1
p11
p12
×××
p1m
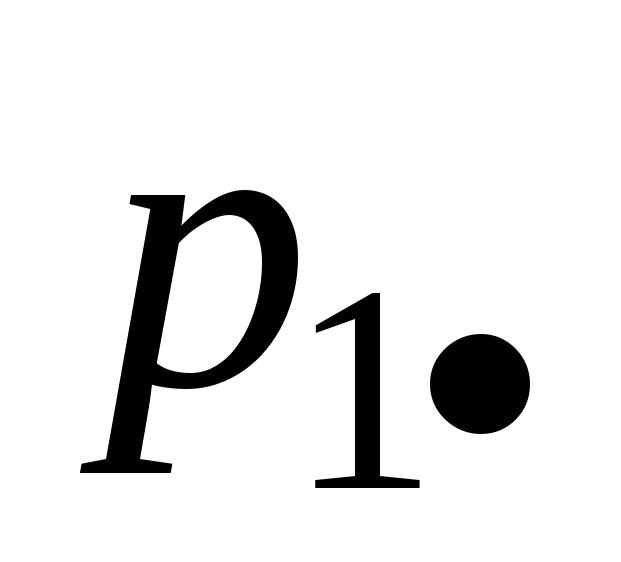
x2
P21
p22
×××
p1m
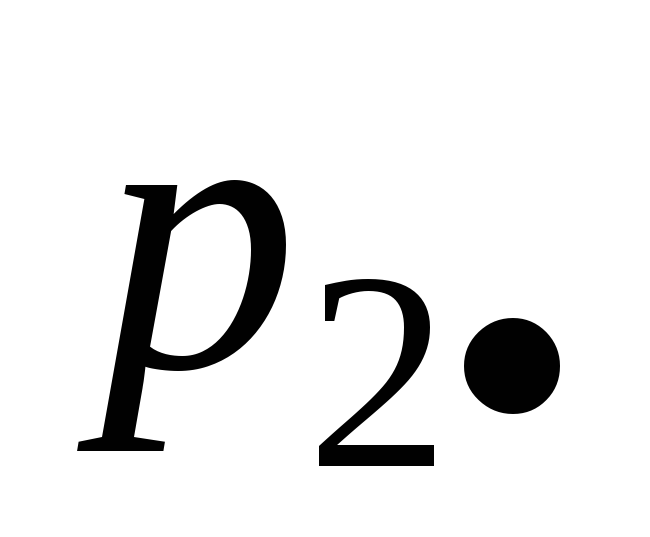
×××
×××
×××
×××
×××
×××
xn
pn1
pn1
×××
Pnm
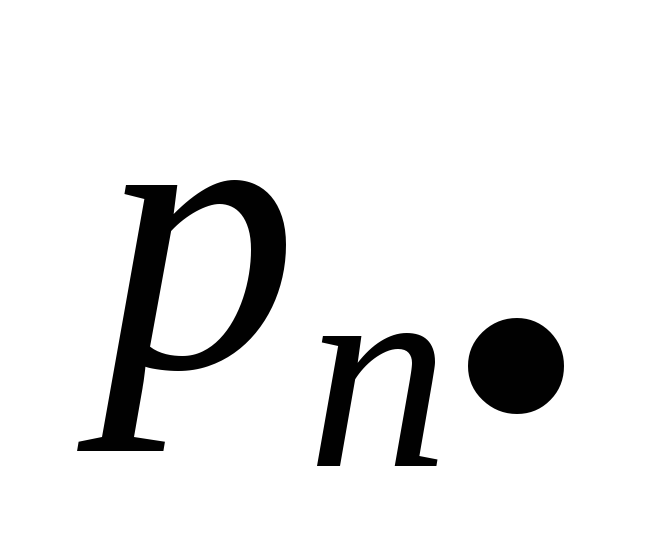
å

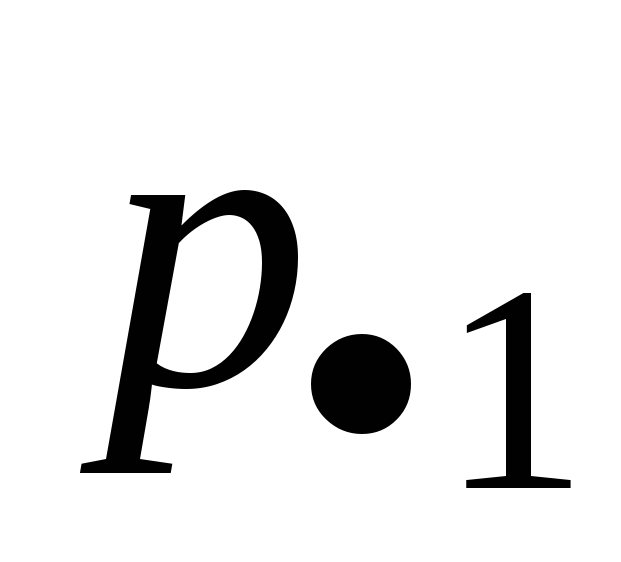
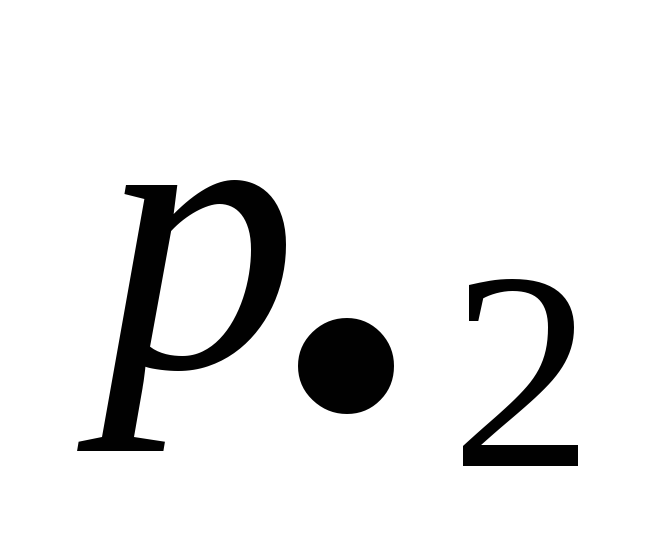
×××
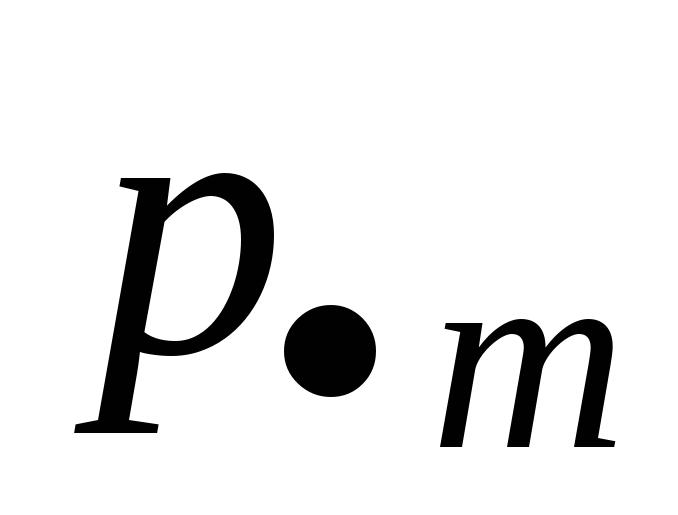
1
