2.1 Условная вероятность

Пусть имеется вероятностное пространство (,U, P). Рассмотрим два события A и B, причем P(B)>0.

Определение. Условной вероятностью события A при условии, что событие B произошло, называется число

. (2.1)

Условную вероятность еще обозначают P_B(A). Фактически условная вероятность при условии выполнения события В рассматривается в новом вероятностном пространстве, где “комплексу условий проведения опыта” (см. начало п.1.1) добавляется еще одно условие, что событие В произошло. Тогда новое пространство элементарных событий будет подмножеством , алгебра событий и вероятности изменятся.

Пример. Рассмотрим опыт К1 событие А – “выпало число, большее трех“. Вероятность Р(А) = 3/6 = 1/2. Пусть событие В – “выпало четное число” произошло. Тогда пространством элементарных событий в новых условиях является {2, 4, 6}. Вероятность события А при условии, что событие B произошло, равно по классическому определению вероятности 2/3, так как число всех элементарных событий в новом пространстве элементарных событий равно 3 и два элементарных события 4 и 6 благоприятствуют событию А. Теперь эту условную вероятность вычислим по определению:

В = {2, 4, 6}  Р(В) = 3/6 = 1/2; AB = {4, 6}  Р(АВ) = 2/6 = 1/3.

.

Как видно, результаты совпали.

Независимость событий.

Определение. Два события A и B называются (вероятностно) независимыми, если

Р(АВ) = Р(А)Р(В) (2.2)

Пусть P(B)>0, A и B независимы. Тогда в силу равенства (2.2) выполняется равенство . Из этого следует, что если событияA и B независимы, то вероятность Р(А) не зависит от того, произошло ли событие В или нет.

В теории вероятности применяется принцип: если события А и В причинно независимы, то они независимы вероятностно.

Докажите утверждение: если события А и В независимы, то независимы пары событий А и ,В и .

Теперь определим понятие независимости нескольких событий.

Определение. События A₁, A₂ , …, А_n (n  2) называются независимыми (в совокупности), если для любого сочетания по k (2  k  n) из этих событий выполняется равенство

.

2.2 Формула умножения вероятностей.

Если события A₁, A₂ , …, А_n (n  2) независимы, то из определения независимости следует формула умножения вероятностей

.

Эта формула читается так: вероятность произведения нескольких независимых событий равна произведению их вероятностей и носит название формулы умножения вероятностей.

Теперь рассмотрим формулу вероятности произведения событий для произвольных событий. Из формулы (2.1) следует

(2.3)

Обобщение этой формулы для n (n  2) событий приводит к формуле

.

2.3 Формула полной вероятности

Пусть для событий H₁, H₂ , …, H_n (n  2) выполнены два условия:

1) они попарно несовместны и имеют ненулевые вероятности;

2) .

Тогда верна формула полной вероятности:

(2.4)

События H₁, H₂ , …, H_n называются гипотезами, а смысл равенства состоит в том, что событиеА может произойти только с одним из гипотез.

Выведем эту формулу. Так как события АН_i (i = 1, …, n ) несовместны, то по формуле сложения вероятностей и формуле (2.3) имеем

,

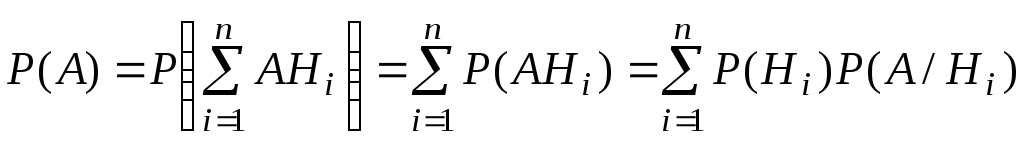что и требовалось доказать.

Задача 2.1 В магазин поступили однотипные телевизоры с 1-го завода 10 шт., со 2-го завода 15 шт. Вероятность изготовить бракованный телевизор на 1-м заводе равна 0,1, на 2-м – 0,2. Случайно отобрали один из поступивших телевизоров. Какова вероятность того, что он бракованный?

Решение. Введем события:

А – «Выбранный телевизор оказался бракованным»,

Н₁– «Выбранный телевизор изготовлен на 1-м заводе»,

Н₂– «Выбранный телевизор изготовлен на 2-м заводе»,

Гипотезы Н₁, Н₂ несовместны и событие А может произойти только с одним из них. Значит можно применить формулу полной вероятности.

P(Н₁)=10/25 = 2/5=0,4; P(A/Н₁) = 0,1;

P(Н₂)=15/25 = 3/5=0,6; P(A/Н₂) = 0,2.