2.4 Формула Байеса

При выполнении для гипотез H₁, H₂ , …, H_n и события А условий 1) и 2) п. 2.3 верна формула Байеса:

, i = 1, …, n. (2.5)

По этим формулам вычисляются так называемые апостериорные вероятности гипотез, то есть вероятности гипотез после того как событие А произошло. Безусловные вероятности гипотез Р(Н_i) называются априорными.

Задача 2.2 При условиях задачи из 2.1 найти вероятность гипотез Н₁, Н₂ ,если известно, что отобранный телевизор оказался бракованным.

Решение. Используя результаты вычислений из решения задачи 2.1, по формуле Байеса имеем:

Как видим, апостериорная вероятность гипотезы Н₁ уменьшилась по сравнению априорной вероятностью. Объяснение простое: поскольку на первом заводе брака делается в два раза меньше, чем на втором, а выбранный телевизор оказался бракованным, то, естественно, вероятность того, что он из 1-го завода уменьшится.

2.5 Схема и формула Бернулли

Схема Бернулли – это независимое многократное повторение одного и того же опыта, который имеет два противоположных события: успех и неудача.

Введем обозначения:

p – вероятность успеха,

q = 1– p – вероятность неудачи,

n – число повторения опыта (n  2),

k – число успехов в n повторениях опыта (k = 0,1, …, n).

Вероятность появления k раз успеха в n независимых повторениях опыта вычисляется по формуле Бернулли:

, (2.6)

где – число сочетаний изn по k.

Вывод формулы Бернулли. Результатом n независимых повторений опыта является произведение n успехов и неудач в совокупности: , где– либо успех, либо неуспех. Если в этом произведенииk успехов и n–k неудач, то по формуле умножения вероятностей

.

Два события вида , имеющие ровноk успехов отличаются тем, что успехи располагаются на разных местах. Если выписать подряд номера мест, соответствующие успехам, то получим сочетание из n по k. Таким образом, событий вида , имеющих ровноk успехов, ровно . Следовательно, по формуле сложения вероятностей

,

где суммирование осуществляется по всем событиям вида , имеющим ровноk успехов.

Пример 2.1.Пятикратное подбрасывание монеты является схемой Бернулли с параметрамиn= 5,p=0.5,q= 0.5. По формуле Бернулли

Пример 2.2.В аппаратуре работают независимо 1000 однотипных элементов. Вероятность выхода каждого из них за время работыTравнаp = 0.005. Эту ситуацию можно рассматривать как схему Бернулли сn= 1000,p=0.005,q= 0.995. Обратите внимание на то, что успехом здесь является “негативное” событие – “Элемент вышел из строя за время работыT”.

По формуле Бернулли Нетрудно понять, что вычисление этого выражения затруднительно. Поэтому необходимы приближенные формулы для вычисления вероятностей.

2.5 Приближенные формулы в схеме Бернулли

Предельная теорема Пуассона

Пусть при так, что. Тогда.

Доказательство. =

=

=

=

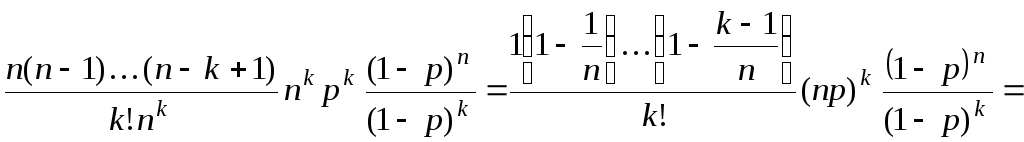
Так как при , , ,

, то .

При больших значениях n и малых p из теоремы Пуассона следует приближенные формулы

, (2.7)

(2.8)

Замечание 2.1 Формулы (2.7) и (2.8) дают приемлемые погрешности при больших значениях n и малых p. В [Чудесенко] рекомендуется применять ее при npq  9, а в [Кремер] – при np10.

Замечание 2.2 Для нахождения значений по формулам (2.7), (2.8) существуют таблицы [Ефимов], [Чудесенко].

Задача 2.3 Вычислить вероятность из примера 2.1.

Величина npq = 10000.0050.995=4.975 < 9, значит формула (2.7) дает хорошую точность. (по таблице III в [Чудесенко]).

Для сравнения приведем точное значение

.

Как видно, погрешность не превышает 0.00007.

Локальная и интегральная формулы Муавра-Лапласа

Для схемы Бернулли при больших n применимы приближенные формулы.

Локальная формула Муавра-Лапласа:

(2.9)

где .

Интегральная формула Муавра-Лапласа:

(2.10)

где – Функция Лапласа.

Замечание 2.3 Формулы (2.9) и (2.10) можно применять при больших значениях n и не очень малых p и q. В [Чудесенко] рекомендуется применять их при npq > 9, а в [Кремер] – при npq  20.

Замечание 2.4 Для нахождения значений по формулам (2.9), (2.10) существуют таблицы [Ефимов], [Чудесенко].

Задача 2.4 Вероятность рождения мальчика в регионе составляет р = 0.51. Какова вероятность того, что из 500 новорожденных в регионе мальчиков не менее 250?

Решение. Имеет место схема Бернулли с параметрами: n =500, p =0.51, q= 0.49.

npq =510.49=24.99 >20, значит, применима интегральная формула Муавра-Лапласа.

.

Значения функции Лапласа взяты из таблицы II [Чудесенко].

Точное значение вероятности равна 0.9611386… . Погрешность составляет около 0.01. Относительно большая погрешность объясняется, по-видимому, небольшим значением n.

Для сравнения погрешностей формул Пуассона и Муавра-Лапласа вычислим по формуле (2.9) вероятность из задачи п. 2.2.

,

(таблица I в [Чудесенко]).

Получилась очень большая погрешность по сравнению с результатом п. 2.7, т.е. в этой задаче локальная формула Муавра-Лапласа не приемлема.