Рассмотрим три закона распределения, которые часто используются в теории вероятностей.

1. Распределение (читается “хи в квадрате”). ПустьÎn(0, 1) – независимые нормально распределенные с.В. С.В. Называетсяраспределенной по закону со степенью свободыk.

2. Распределение Стьюдента т(k). С.В. , гдеU în(0, 1), называется распределенной по закону Стьюдента со степенью свободы k.

3. С.В. , гдеk1, k2 – натуральные числа, называется распределенной по закону Фишера со степенями свободы k1, k2.

Рисунок 7.6

В математической статистике важную роль играет понятие квантили, введенное в лекции 4.Квантилью порядкаa(0<a<1) называется такое числоx_a, что

F(x_a)= a. В случае непрерывно распределенной с.в. с плотностью распределения p(x) F(x_a)= P(X<x_a) = . Это значит, что квантильx_a – точка на оси х, в которой вертикаль отсекает слева от себя на графике плотности распределения криволинейную трапецию с площадью a (см. рис. 7.1). Если плотность распределения четная функция, т.е. ее график симметричен относительно оси у, то

x_a= – x_{1– a} (рис. 7.1). Квантили введенных выше распределений можно найти в таблицах в учебниках по теории вероятностей и математической статистике [ ].

7.4.1 Доверительный интервал для м.О. Нормально распределенной с.В.

1) Пусть г.с. XÎN(m,s) и известна дисперсия s ². Воспользуемся тем фактом, что с.в. . Зададим малый уровень значимости 2a. Очевидно, что значения с.в. U попадают в интервал (u_a, u_{1– a}) c вероятностью g =1–2a:

.

Здесь u_a– квантиль распределения с.в. U порядка a.

Теперь, решив неравенства относительноm, получим

. Но так как u_a = – u_{1– a}, то . Далее изg =1–2a имеем 1–a =. Таким образом, окончательно получаем доверительный интервал

.

2) Пусть г.с. XÎN(m,s) и дисперсия s ² не известна. Тогда аналогично, используя точечную оценку S² для дисперсии, получим доверительный интервал

,

где – квантиль распределения Стьюдента порядкасо степенью свободыn–1, S² – исправленная выборочная дисперсия.

7.4.2 Доверительный интервал для дисперсии нормально распределенной г.С.

Пусть м.о. m не известно. Воспользуемся известным фактом, что с.в.

имеет распределение . Пусть – квантиль распределения порядка a. По определению квантили

.

Решив двойное неравенство в скобках относительно , и, учитываяg =1–2a, получим доверительный интервал для дисперсии

.

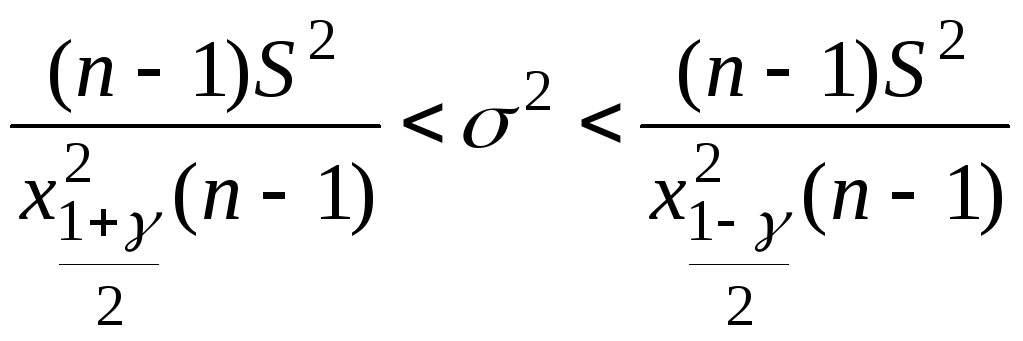Извлекая корень квадратный, из этих неравенств получим доверительный интервал для среднеквадратического отклонения

.

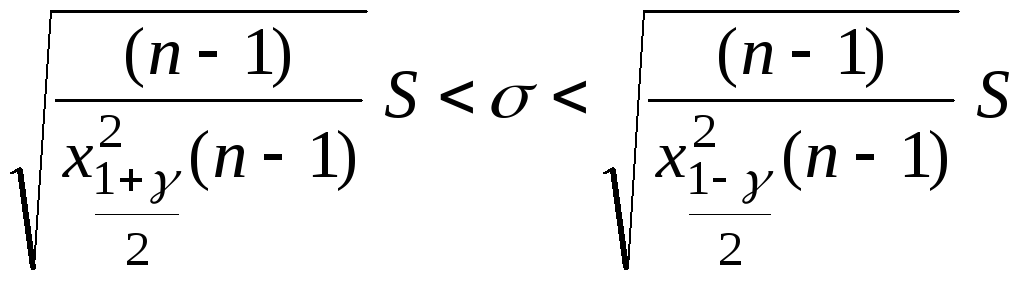Лекция 8

Проверка статистических гипотез

8.1 Предварительная обработка реализации выборки

Рассмотрим основные понятия, связанные с реализацией выборки. Пусть имеется реализация выборки объема n. Если упорядочить значения по возрастанию, то полученная цепочка чисел называетсявариационным рядом.

Пусть x_i – элемент вариационного ряда. Тогда число повторений этого элемента в реализации выборки называется частотой выборочного значенияx_i и обозначаетсяn_i.Величина называетсяотносительной частотойзначенияx_i.

Выделим очевидные равенства

, . (8.1)

Пусть x₁,x₂, …,x_m – все различные значения вариационного ряда, упорядоченные по возрастанию. Таблица

x1	x2	…	xm
n1	n2	…	nm

называется статистическим рядом. Он в некотором смысле характеризует закон распределения г.с.

Теперь предположим, что объем выборки большой. В этом случае строят так называемый интервальный (или группированный) статистический ряд. Рассмотрим реализацию выборки x₁, x₂, …, x_n объема n. Выбираем некоторый отрезок I (обычно это либо отрезок [min{x_i}, max{x_i}], либо чуть больший, чем он). Делим отрезок I точками z₀, z₁, …, z_k. на равные частичные промежутки D₁=[z₀, z₁[, D₂= [z₁ z₂[, …, D_k=[z_k–1 z_k]. Здесь z₀ и z_k – начало и конец отрезка I соответственно. Частотой n_i i-го промежутка D_i называется число значений реализации выборки, попавших в D_i (i=1,2,…, k). Интервальным статистическим рядом называется таблица

D1	D2	…	Dk
n1	n2	…	nk

Проверьте, что для частот и относительных частот выполняется равенства (8.1).

Статистической (или эмпирической) функцией распределения называется

.

Теорема. Если F(x) – функция распределения г.с., то для любого действительного значения x и любого e >0 выполняется равенство

.

Смысл этой теоремы в том, что при больших объемах выборки значения статистической функции распределения является приближенными значениями функция распределения, т.е. статистическая функция распределения является оценкой неизвестной функция распределения г.с.

Для непрерывно распределенной г.с. наглядную оценку для плотности распределения дает гистограмма относительных частот.

Гистограмма относительных частот – это ступенчатая фигура, построенная следующим образом. На оси Ох откладываются частичные промежутки D₁,…, D_k. Над каждым из них строится прямоугольник с высотой n_i / h, где h – длина частичного промежутка. Функция, график которой задается гистограммой относительных частот, также называется гистограммой относительных частот.

Вычислим площадь, «ограниченной» гистограммой.

.

Это аналог свойства нормировки плотности распределения. Оказывается, что гистограмма относительной частоты равна приближенно неизвестной плотности непрерывно распределенной г.с., т.е. гистограмма дает приближенно представление о виде плотности распределения г.с.

Пример 8.1. Дан интервальный статистический ряд

(1, 3)	(3, 5)	(5, 7)	(7, 9)	(9, 11)
10	32	20	24	14

Построить график статистической функции распределения и гистограмму относительных частот. Построить, соответственно, приближенные графики неизвестных функции и плотности распределения г.с.

Объем выборки n=100. Длина h частичного промежутка равна 2. Относительные частоты равны n₁=10/100=0.1, n₂=32/100=0.32, n₃=0.2, n₄=0.24, n₅=0.14.

Вычислим значения статистической функции распределения:

На рисунке 8.1 приведены график статистической функции распределения и приближенно график функции распределения.