
- •Теория вероятностей и математическая статистика
- •1.2 События и действия (операции) над ними.
- •1.3 Классическое определение вероятности
- •1.4. Свойства вероятностей
- •1.5. Формула сложения вероятностей
- •Эта формула называется формулой сложения вероятностей для несовместных событий и читается так: вероятность суммы нескольких попарно несовместных событий равна сумме их вероятностей.
- •1.6. Статистическое и геометрическое определения вероятности
- •Геометрическое определение вероятности.Вероятностью событияА называется.
- •1.7. Понятие об аксиоматическом определении вероятности.
- •2.1 Условная вероятность
- •2.2 Формула умножения вероятностей.
- •2.3 Формула полной вероятности
- •2.4 Формула Байеса
- •2.5 Схема и формула Бернулли
- •2.5 Приближенные формулы в схеме Бернулли
- •Лекция 3
- •3.1 Случайная величина
- •3.2 Дискретные случайные величины
- •3.4 Непрерывные случайные величины
- •Свойства плотности вероятности.
- •Смысл дисперсии в том, что она является мерой рассеяния значений случайной величины от математического ожидания. Чем меньше дисперсия, тем меньше разброс значений от математического ожидания.
- •4.4 Свойства дисперсии
- •4.5 Другие числовые характеристики
- •4.6 Нормальное распределение (распределение Гаусса)
- •Лекция 5
- •5.1 Числовые характеристики некоторых распределений
- •Равномерное распределение.
- •Непрерывно распределенные двумерные случайные величины
- •6.3 Корреляционный момент, коэффициент корреляции
- •6.4 Представление о законе больших чисел
- •6.5 Представление о центральной предельной теореме
- •Лекция 7
- •Рассмотрим три закона распределения, которые часто используются в теории вероятностей.
- •1. Распределение (читается “хи в квадрате”). ПустьÎn(0, 1) – независимые нормально распределенные с.В. С.В. Называетсяраспределенной по закону со степенью свободыk.
- •2. Распределение Стьюдента т(k). С.В. , гдеU în(0, 1), называется распределенной по закону Стьюдента со степенью свободы k.
- •3. С.В. , гдеk1, k2 – натуральные числа, называется распределенной по закону Фишера со степенями свободы k1, k2.
- •7.4.1 Доверительный интервал для м.О. Нормально распределенной с.В.
- •7.4.2 Доверительный интервал для дисперсии нормально распределенной г.С.
- •8.1 Предварительная обработка реализации выборки
- •F*(X) – статистическая функция распределенияр(X) – плотность распределения
- •8.2 Основные понятия проверки статистических гипотез
- •Лекция 9. Элементы регрессионного анализа
- •9.1 Парный линейный регрессионный анализ.
- •9.2 Парный обобщенный линейный регрессионный анализ
F(x)
– функция распределения
Рисунок
8.7 Рисунок
8.2
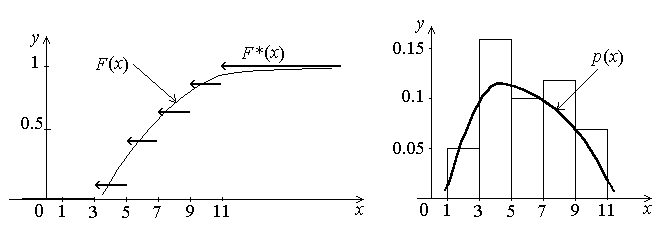
F*(X) – статистическая функция распределенияр(X) – плотность распределения
8.2 Основные понятия проверки статистических гипотез
Во многих практических задачах реализации выборки применяются для проверки гипотез (предположений) о свойствах закона распределения генеральной совокупности.
Определение. Статистической гипотезой называется предположение о параметрах, свойствах закона распределения генеральной совокупности.
Пример 8.2 “Математическое ожидание г.с., распределенной по показательному закону, равно 10”, ”Г.с. имеет нормальный закон распределения” – статистические гипотезы. “Завтра будет снег”, “Существуют внеземные цивилизации” – не являются статистическими гипотезами.
В дальнейшем под гипотезой будем понимать исключительно статистические гипотезы. Гипотеза называется простой, если она однозначно определяет закон распределения г.с. В противном случае гипотеза называется сложной. В приведенных выше гипотезах первая – простая, потому, что гипотеза определяет точно один показательный закон распределения с параметром l = 1/10. Вторая гипотеза является сложной, потому что она определяет бесконечно много нормальных законов распределения с разными математическими ожиданиями и дисперсиями.
Параметрическими гипотезами называются гипотезы о параметрах распределения г.с. Например, первая из вышеприведенных гипотез является параметрической.
Нулевой (или основной) гипотезой H0 называется проверяемая гипотеза. Альтернативной (или конкурирующей) гипотезой называется, гипотеза, которая принимается в случае, когда основная гипотеза отвергается. Альтернативных гипотез у одной и той же основной гипотезы может быть несколько. Например, если принять за основную гипотезу “Математическое ожидание г.с. равно 10”, то в качестве альтернативной могут быть: “Математическое ожидание г.с. меньше 10”, ”Математическое ожидание г.с. равно 9”.
При проверке гипотез применяется некоторое правило. Критерием K проверки гипотез называется правило, по которому принимается или отвергается гипотеза H0. Обычно в критерии участвует некоторая статистика Z=Z(X1, …, Xn), по значению которой решается вопрос, принять или отвергнуть основную гипотезу. Z называется статистикой критерия.
Общая схема критерия K выглядит следующим образом. Задается некоторая малая вероятность a (обычно a = 0.1, 0.05, 0.01), называемая уровнем значимости критерия. В основе критерия лежит принцип теории вероятностей: маловероятные события (события с вероятностью a ) считать практически невозможными. Из области значений V статистики Z критерия выделяется подмножество Vk, такое, что условная вероятность события ZÎ Vk при условии, что гипотеза H0 верна, мала (равна a ): P (ZÎ V k / H0 ) = a. Множество Vk называется критической областью. Пусть теперь по реализации выборки вычислено значение zв статистики критерия Z. Если zвÎ Vk , то это означает, что произошло маловероятное событие. Тогда по приведенному выше принципу скорей всего неверна гипотеза H0 и она должна быть отвергнута. Если zвÎ V \ Vk , то гипотеза H0 может быть принята. Множество V \ Vk называется область принятия основной гипотезы.
Рассмотрим критерий проверки параметрической гипотезы H0 :q =q 0 при альтернативной гипотезеH1:q <q0. Пустьp (z/ H0 ) – плотность условного закона распределения статистикиZ. За область принятия основной гипотезы принимается такой промежуток [z1, +¥), чтоP (Z ³z1/H0 ) = 1–a,P (Z < z1/H0 ) =a (рис. 8.3).
Из второго равенства видно, что z1= za– квантиль распределения статистикиZпорядкаa.
Рисунок 8.3
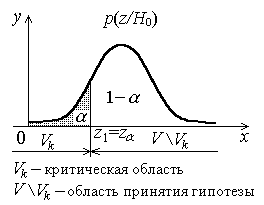
[za , +¥).
Критерий состоит в следующем. По реализации выборки из г.с. вычисляем значение zв статистики критерия Z. Вычисляются (по таблице) квантиль za. Если zв ³za, то основная гипотеза q =q 0 принимается. Если zв< za , то основная гипотеза q =q0 отвергается (принимается альтернативная гипотеза q <q0).
Пример 8.3
Расход бензина автомобиля составляет
m=10
л. на 100 км. После модернизации двигателя
проведено испытания с 25 автомобилями
и получено выборочное среднее расхода
бензина
![]() л. на 100 км. Считая расход бензинаX
нормально распределенной случайной
величиной c
дисперсией
л. на 100 км. Считая расход бензинаX
нормально распределенной случайной
величиной c
дисперсией
![]() ,
проверить основную гипотезуH0
: m=10
на уровне значимости a
= 0.05 при
альтернативной гипотезе H1
: m
<10.
,
проверить основную гипотезуH0
: m=10
на уровне значимости a
= 0.05 при
альтернативной гипотезе H1
: m
<10.
Из условий задачи
следует, что если гипотеза m=10
верна, то г.с. X
распределена
нормально с математическим ожиданием
m=10
и дисперсией
![]() .
Тогда
известно
[
], что
случайная
величина
.
Тогда
известно
[
], что
случайная
величина
![]() имеет стандартное нормальное распределение.
В качестве статистики критерия возьмем
эту случайную величину. Квантиль
распределения случайной величины U
порядка a
= 0.05 найдем
по таблице N
[ ] u0.05
= – u0.95
= –1.645.
имеет стандартное нормальное распределение.
В качестве статистики критерия возьмем
эту случайную величину. Квантиль
распределения случайной величины U
порядка a
= 0.05 найдем
по таблице N
[ ] u0.05
= – u0.95
= –1.645.
Вычислим выборочное
значение критерия U:
![]() .
.
Так как uв= –1.75< ua= –1.645, то uв попало в критическую область, поэтому основная гипотеза m=10 отвергается и принимается альтернативная гипотеза m <10. Таким образом, можно сделать практический вывод: с вероятностью 0.95 можно утверждать, что модернизация двигателя действительно привела к уменьшению расхода бензина.
Как видно, основная или альтернативная гипотезы принимаются или отвергаются с некоторой вероятностью. Это означает, что возможны ошибки при принятии того или иного решения. В теории проверки статистических гипотез различают ошибки первого и второго рода.
Ошибкой первого рода называется вероятность отвергнуть правильную основную гипотезу, т.е. P (ZÎVk / H0 ) = a. Таким образом, уровень значимости совпадает с ошибкой первого рода.
Ошибкой второго рода называется вероятность принять ошибочную основную гипотезу, т.е. P (ZÎV\Vk / H1 ) =b.
8.3 Критерий согласия Х 2
Критерием согласия называют критерии проверки статистических гипотез о виде закона распределения г.с. Примером статистической гипотезы о виде закона распределения г.с. X является : “Г.с. X имеет нормальный (равномерный и т.д.) закон распределения”. Такая гипотеза принимается за основную гипотезу H0.
Рассмотрим подробно эффективный критерий согласия Пирсона Х2 (критерий хи-в-квадрате).
Пусть проверяется
гипотеза “Г.с. X
имеет
гипотетическую функцию распределения
![]() ”,
где
”,
где![]() –
неизвестные параметры распределения,
вид функцииF
известен, l
³1.
Рассмотрим случай непрерывного
распределения.
–
неизвестные параметры распределения,
вид функцииF
известен, l
³1.
Рассмотрим случай непрерывного
распределения.
На первом этапе по реализации выборки объема n строится интервальный статистический ряд с k = [1+3.32lg n] +1 частичными промежутками (см. п. 8.1). Пусть получены равные промежутки с границами в точках
![]() .
Рассмотрим промежутки
.
Рассмотрим промежутки
![]() .
(8.2)
.
(8.2)
Пусть по выборке
найдены точечные оценки неизвестных
параметров
![]() (методом максимального правдоподобия).
Тогда при помощи гипотетической функции
распределения можно найти вероятности
(методом максимального правдоподобия).
Тогда при помощи гипотетической функции
распределения можно найти вероятности
![]()
![]() (8.3)
(8.3)
![]() .
.
Известно, что при достаточно больших значениях объема выборки n случайная величина
![]() (8.4)
(8.4)
имеет
распределение близкое к распределению
![]() – хи-в-квадрате со степенью свободы s =
k– l –1,
где k –
число интервалов, l
– число
неизвестных параметров, замененных их
точечными оценками, mi
– частота
i-го
интервала. Если основная гипотеза верна,
то величина npi
будет близка к частоте ni,
то есть сумма
– хи-в-квадрате со степенью свободы s =
k– l –1,
где k –
число интервалов, l
– число
неизвестных параметров, замененных их
точечными оценками, mi
– частота
i-го
интервала. Если основная гипотеза верна,
то величина npi
будет близка к частоте ni,
то есть сумма
![]() будет мала. В качестве статистики
критерия выбирается случайная величина
будет мала. В качестве статистики
критерия выбирается случайная величина![]() .
Тогда при заданном уровне значимостиa
основная гипотеза отвергается, когда
.
Тогда при заданном уровне значимостиa
основная гипотеза отвергается, когда
![]() .
Это равенство эквивалентно
.
Это равенство эквивалентно![]() .
А это означает, что
.
А это означает, что![]() – квантиль распределенияхи-в-квадрате
порядка 1–a
со степенью свободы
s =
k– l – 1.
– квантиль распределенияхи-в-квадрате
порядка 1–a
со степенью свободы
s =
k– l – 1.
Таким образом,
если выборочное значение
![]() статистики
статистики![]() окажется меньше квантили
окажется меньше квантили![]() ,
то основная гипотеза принимается.
,
то основная гипотеза принимается.
Сформулируем кратко критерий проверки гипотезы о виде закона распределения г.с.
1) По данной реализации выборки построить интервальный статистический ряд, найти промежутки (8.2).
2) Вычислить по
реализации выборки точечные оценки
неизвестных параметров
![]() .
.
3) Вычислить величины npi (i = 1, …, k) по формулам (8.3). Проверить выполнение условий npi ³ 5. Если для некоторых интервалов это условие нарушается, то этот интервал объединяется с соседним (при этом складываются вероятности pi и частоты этих интервалов). Эта процедура продолжается до тех пор пока для всех интервалов не будет выполняться условие npi ³ 5.
4)
По формуле (8.4) вычислить выборочное
значение![]() статистики
статистики![]() .
.
5) По таблице найти
квантиль
![]() распределенияхи-в-квадрате
порядка 1–a
со степенью свободы
s =
k– l – 1, где
k –
число интервалов после пересчета в
пункте 3, l –
число
неизвестных параметров, замененных их
точечными оценками в пункте 2.
распределенияхи-в-квадрате
порядка 1–a
со степенью свободы
s =
k– l – 1, где
k –
число интервалов после пересчета в
пункте 3, l –
число
неизвестных параметров, замененных их
точечными оценками в пункте 2.
6) Если
![]() <
<![]() ,
то основная гипотеза принимается на
уровне значимостиa
; если
,
то основная гипотеза принимается на
уровне значимостиa
; если
![]() ³
³![]() ,
то основная гипотеза отвергается.
,
то основная гипотеза отвергается.
