1.3 Классическое определение вероятности

Пусть  – конечно, все элементарные события равновозможны.

Определение. Вероятностью события А называется число

, (1.1)

где n – число всех элементарных событий в , m – число элементарных событий, благоприятствующих событию А (т.е. входящих в А).

1.4. Свойства вероятностей

Основные свойства вероятности.

1. P(A)0 для любого события A;

2. P()=1;

3. если события A₁, A₂ , …, A_n несовместны, то

P(A₁ + A₂ + …+ A_n) = P(A₁)+P(A₂ )+ …+P(A_n).

Действительно, т.к. m  0 и n > 0, то из (1.1) следует P(A)0.

Для  все элементарные события благоприятствуют этому событию, поэтому m = n и .

Свойство 3 называется свойством адитивности вероятности. Докажем для случая двух событий. Пусть событию A₁ благоприятствуют k₁, событию A₂ – k₂ элементарных событий. Поскольку A₁ и A₂ несовместны, то событию A₁+A₂ благоприятствуют k₁ + k₂ элементарных событий. Тогда

Для более двух событий теорема доказывается по индукции.

Другие свойства вероятности.

4. 0  P(А)  1 для любого события А;

5. Если А  В, то P(А)  P(В);

6. P(А + В)  P(А) + P(В);

7. ;

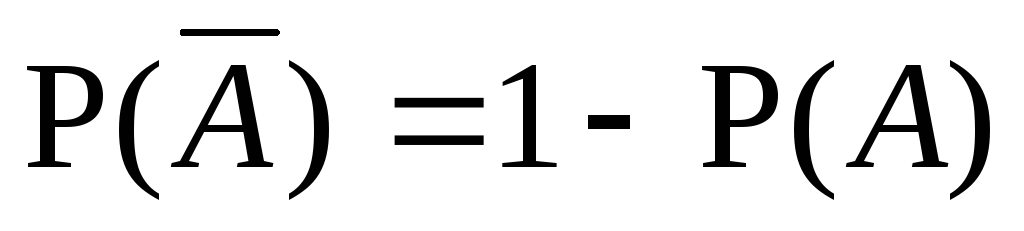8. P() = 0;

Предоставляем студентам доказать эти свойства, исходя из классического определения вероятности.

1.5. Формула сложения вероятностей

Пусть события A₁, A₂ , …, A_n несовместны. Тогда по свойству адитивности

P(A₁ + A₂ + …+ A_n) = P(A₁) + P(A₂ ) + …+ P(A_n). (1.2)

Эта формула называется формулой сложения вероятностей для несовместных событий и читается так: вероятность суммы нескольких попарно несовместных событий равна сумме их вероятностей.

Пусть теперь A₁,A₂– произвольные события иA₁содержитk₁, событиеA₂–k₂, произведениеA₁A₂ –k элементарных событий. Тогда элементарные события изA₁A₂ входят вA₁ и вA₂. Значит, вA₁+A₂ входят вk₁+k₂ – k элементарных событий. Следовательно, получается формула

P(A₁ + A₂) = P(A₁) + P(A₂ ) – P(A₁A₂). (1.3)

Эту формулу можно обобщить на любое конечное число событий:

P(A₁+A₂ + …+A_n) =

= P(A₁) + P(A₂ ) + …+ P(A_n) – (P(A₁ A₂) + …+ P(A_n–1 A_n)) +…+ (–1)^n–1 P(A₁ A₂ …A_n).

1.6. Статистическое и геометрическое определения вероятности

Пусть в результате некоторого опыта может появиться событие А. Обозначим m_n – число появления этого события в n повторениях этого опыта. Отношение

называется относительной частотой события А.

Статистическое определение вероятности. Предел , если он существует, называется вероятностью событияА : .

Практика показывает, что относительная частота событияА стабилизируется с возрастанием числа n, что гарантирует существование указанного предела.

Недостаток классического определения вероятностей состоит в том, что оно применимо только в конечных пространствах элементарных событий и от элементарных событий требуется их “равновозможность”. Статистическое определение не требует указанных ограничений, но его теоретическая непригодность состоит в том, что невозможно точно вычислить вероятность события, поскольку относительная частота вычисляется из опытных данных.

Пример. А – “Выпал “орел” при бросании симметричной монеты”. Относительная частота этого события при большом числе подбрасывании монеты равна примерно 0,5. Статистическую вероятность этого события можно считать равной 0,5.

Пусть теперь пространство элементарных событий состоит из всех точек некоторой “измеримой” области  и выбор каждой ее точки “равновозможен”. “Равновозможность” здесь понимается в том смысле, что степень возможности выбрать точку из подмножества А   пропорциональна ее мере и не зависит от ее формы и расположения. Событием называется любое “измеримое” подмножество А . Под мерой множества понимается его длина, площадь, объем в зависимости от того, является ли  подмножеством соответственно одномерного, двумерного, трехмерного пространства. Множество называется “измеримым”, если для него существует мера(т.е. длина, площадь, объем).