Лекция 3

3.1 Случайная величина

Пусть имеется вероятностное пространство .

Случайной величиной называется измеримая числовая функция . Измеримая числовая функция– это функция, удовлетворяющая следующему условию:множество, т.е. оно является событием.

В соответствии с определением случайной величины вводится числовая функция F(x), определенная для каждого действительного x и по определению равная вероятности наступления события: Эта функция называется функцией распределения случайной величины. В дальнейшем событиебудем обозначать сокращенно.

Из измеримости случайной величины следует, что большинство подмножеств элементарного пространства , задаваемые «простыми» равенствами и неравенствами, являются событиями. Так, множества вида ,,,являются событиями.

Говорят, что для случайной величины задан закон ее распределения, если известна такая функция, при помощи которой можно найти вероятность любого события, «порождаемого» этой случайной величиной. Функция распределения как раз задает закон распределения случайной величины.

Свойства функции распределения.

Пусть F(x) – функция распределения случайной величины

1) ;

2) ;

3) F(x) – неубывающая функция;

4) F(x) непрерывна слева;

5) .

Доказательство. Неравенства 1 следуют из того, что F(x) – вероятность. Событие , а, следовательно, свойства 2 следуют из равенствЕслиx < t, то . Следовательно, из свойства вероятности следует, что. Доказательство 4 опускаем. Докажем свойство 5.+=и событияинесовместны, значит=+. Откуда следует.

3.2 Дискретные случайные величины

Случайные величины в дальнейшем будем обозначать большими латинскими буквами: X, Y, Z, … .

Случайная величина называется дискретной, если в результате испытания она может принять значение из конечного либо счетного множества возможных числовых значений. Будем пользоваться сокращением ДСВ для обозначения дискретной случайной величины.

Закон распределения ДСВ Х можно задать в виде функции, ставящей в соответствие каждому значению x_i ее вероятность p_i = P(X = x_i), причем .

Когда различных значений ДСВ конечно и равно n, то ее закон распределения задается в виде таблицы ():

x1	x2	…	xn
p1	p2	…	pn

Очевидно, должно выполняться равенство .

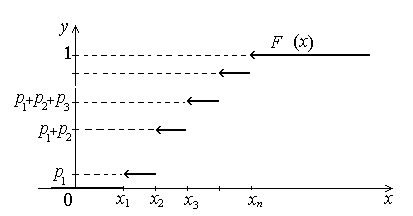
Построим функцию распределения для ДВС. По определению

.

График функции распределения ДВС

Рисунок 3.2

т.е. для любого действительного х значение F(x) численно равно вероятности наступления следующего события: в результате испытаний над X она приняла значение строго меньшее x. Эта функция является кусочно-постоянной (ступенчатой), ее график см. на рисунке 3.1.

Пример 3.1 Х – число очков, выпавшее при однократном вбрасывании игрального кубика. Закон распределения Х имеет вид

1	2	…	6
		…

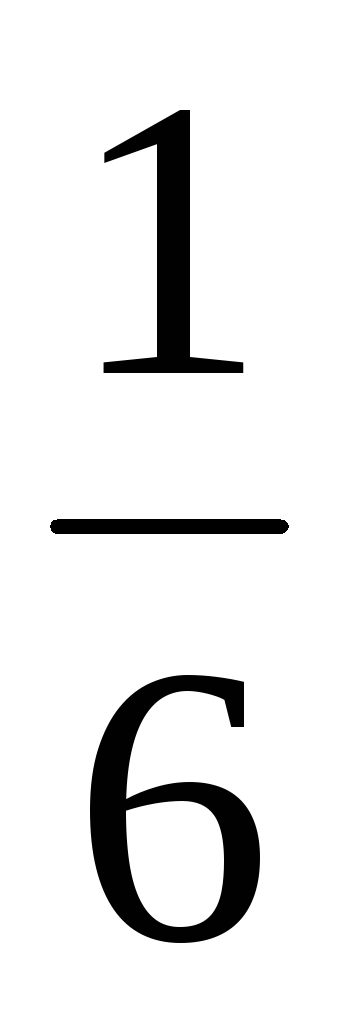
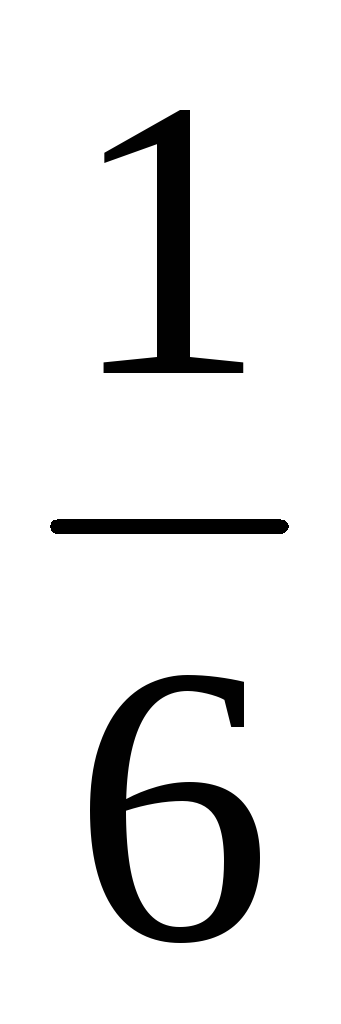
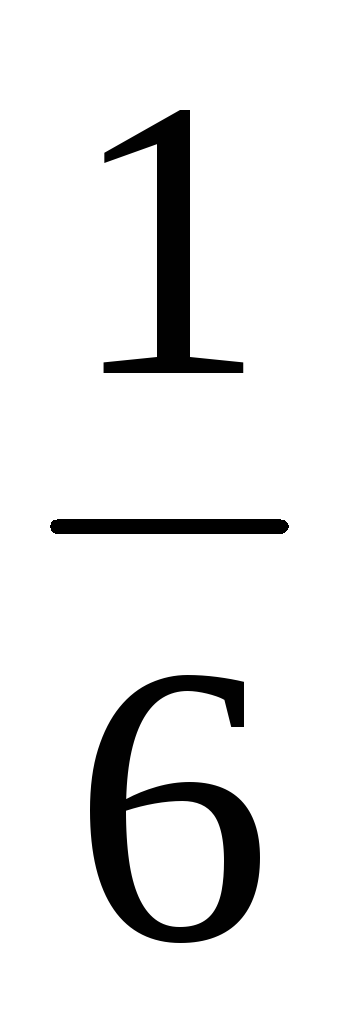
Это так называемое равномерное дискретное распределение.

Пример 3.2 Х – число успехов в схеме Бернулли. Пусть n – число испытаний, p – вероятность успеха, q=1–p. Тогда закон распределения случайной величины Х задается соответствием ,i=1, …, n. Студенту предлагается доказать, что . Этот закон называетсябиномиальным и будем в дальнейшем обозначать B(n,p).

Пример 3.3 Х – число обращений клиентов в сервисный центр по ремонту бытовой техники фирмы SONY (см. пример 1.2). Из практики следует, что закон распределения имеет вид ,i = 0, 1, … . Это распределение называется распределением Пуассона и будем в дальнейшем обозначать P(). Студенту предлагается доказать, что .