
- •Теория вероятностей и математическая статистика
- •1.2 События и действия (операции) над ними.
- •1.3 Классическое определение вероятности
- •1.4. Свойства вероятностей
- •1.5. Формула сложения вероятностей
- •Эта формула называется формулой сложения вероятностей для несовместных событий и читается так: вероятность суммы нескольких попарно несовместных событий равна сумме их вероятностей.
- •1.6. Статистическое и геометрическое определения вероятности
- •Геометрическое определение вероятности.Вероятностью событияА называется.
- •1.7. Понятие об аксиоматическом определении вероятности.
- •2.1 Условная вероятность
- •2.2 Формула умножения вероятностей.
- •2.3 Формула полной вероятности
- •2.4 Формула Байеса
- •2.5 Схема и формула Бернулли
- •2.5 Приближенные формулы в схеме Бернулли
- •Лекция 3
- •3.1 Случайная величина
- •3.2 Дискретные случайные величины
- •3.4 Непрерывные случайные величины
- •Свойства плотности вероятности.
- •Смысл дисперсии в том, что она является мерой рассеяния значений случайной величины от математического ожидания. Чем меньше дисперсия, тем меньше разброс значений от математического ожидания.
- •4.4 Свойства дисперсии
- •4.5 Другие числовые характеристики
- •4.6 Нормальное распределение (распределение Гаусса)
- •Лекция 5
- •5.1 Числовые характеристики некоторых распределений
- •Равномерное распределение.
- •Непрерывно распределенные двумерные случайные величины
- •6.3 Корреляционный момент, коэффициент корреляции
- •6.4 Представление о законе больших чисел
- •6.5 Представление о центральной предельной теореме
- •Лекция 7
- •Рассмотрим три закона распределения, которые часто используются в теории вероятностей.
- •1. Распределение (читается “хи в квадрате”). ПустьÎn(0, 1) – независимые нормально распределенные с.В. С.В. Называетсяраспределенной по закону со степенью свободыk.
- •2. Распределение Стьюдента т(k). С.В. , гдеU în(0, 1), называется распределенной по закону Стьюдента со степенью свободы k.
- •3. С.В. , гдеk1, k2 – натуральные числа, называется распределенной по закону Фишера со степенями свободы k1, k2.
- •7.4.1 Доверительный интервал для м.О. Нормально распределенной с.В.
- •7.4.2 Доверительный интервал для дисперсии нормально распределенной г.С.
- •8.1 Предварительная обработка реализации выборки
- •F*(X) – статистическая функция распределенияр(X) – плотность распределения
- •8.2 Основные понятия проверки статистических гипотез
- •Лекция 9. Элементы регрессионного анализа
- •9.1 Парный линейный регрессионный анализ.
- •9.2 Парный обобщенный линейный регрессионный анализ
3.4 Непрерывные случайные величины
Будем рассматривать пространство элементарных событий как совокупность всех точек числовой оси. Случайная величина X называется непрерывно распределенной (или непрерывной), если ее функция распределения является непрерывной. Для непрерывной случайной величины примем сокращение НСВ.
Примеры. X – время безотказной работы телевизора (см. пример 1.3). X – рост взрослого человека.
Пусть X – НСВ. Найдем вероятность того, что в результате испытаний случайная величина X примет значение a R. Докажем, что P(X = a)=0.
Так как
![]() ,
то
,
то![]() .
.
Следовательно
![]()
=![]() .
.
Заметим, что в случае ДСВ вероятность P(X = a) не всегда равна нулю.
Плотность распределения вероятности НВС.
Ранее говорилось, что функция распределения задает закон распределения случайной величины. Для НСВ удобнее закон распределения задавать при помощи плотности распределения вероятности. Плотностью распределения вероятности НСВ Х называется предел (если он существует)
![]() .
.
Таким образом, плотность распределения является первообразной для функции распределения.
Свойства плотности вероятности.
Плотность вероятности является неотрицательной функцией.
Действительно, производная неубывающей функции неотрицательна.
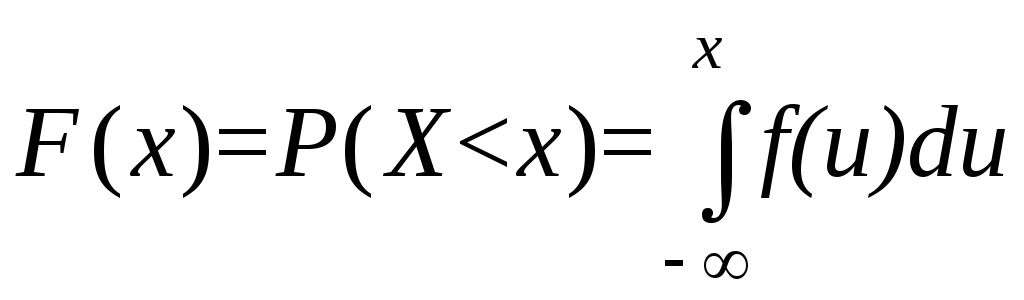 .
Это следует из того, что плотность
распределения является первообразной
для функции распределения.
.
Это следует из того, что плотность
распределения является первообразной
для функции распределения.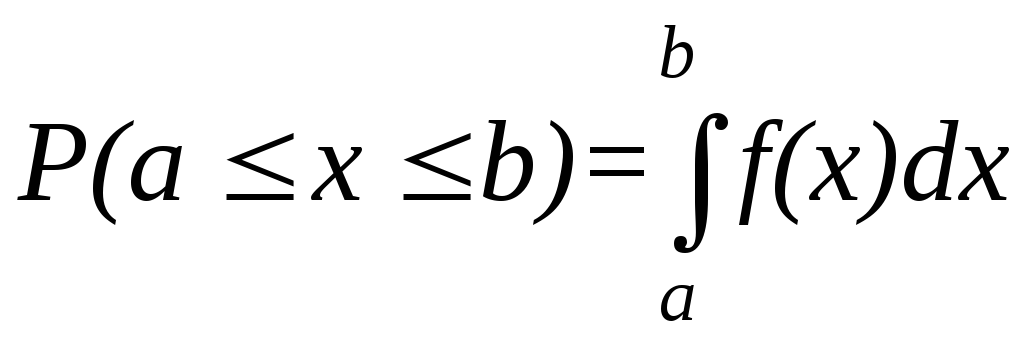 .
Это следует из формулы Ньютона-Лейбница:
.
Это следует из формулы Ньютона-Лейбница:
![]()
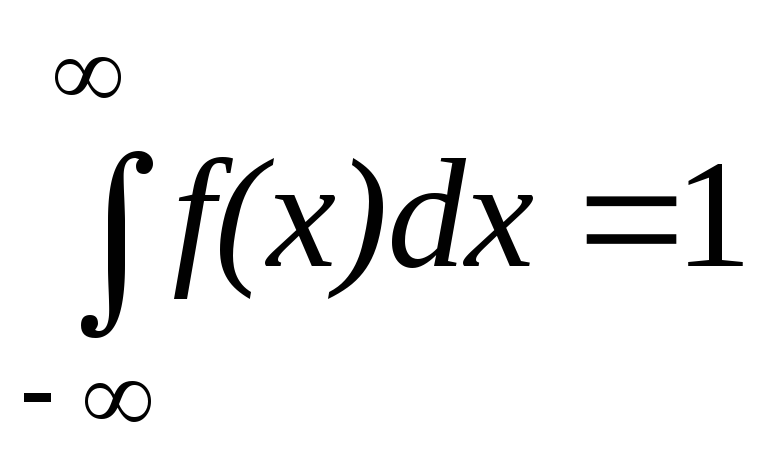 .
Это свойство называется свойством
нормировки.
.
Это свойство называется свойством
нормировки.
Действительно,![]() .
.
Пример 3.4 Случайная величина Х называется равномерно распределенной на отрезке [a, b], если ее плотность распределения имеет вид
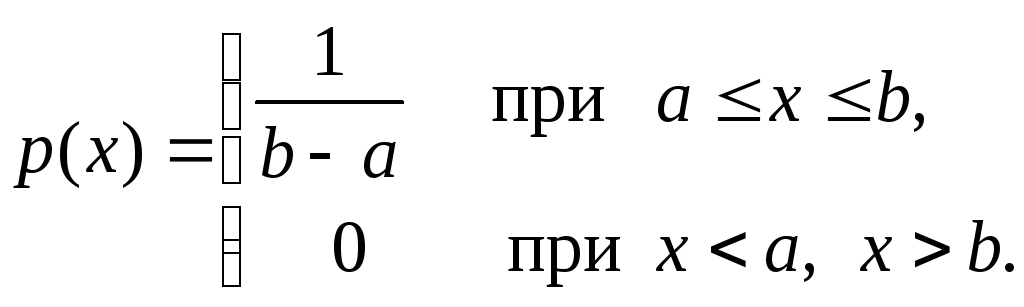
В дальнейшем равномерное распределение будем обозначать R(a, b).
Рисунок
3.3
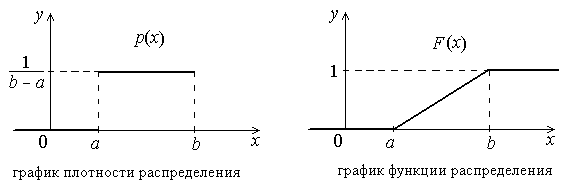
Пример 3.5 Экспоненциальное (или показательное) распределение имеет плотность распределения вида
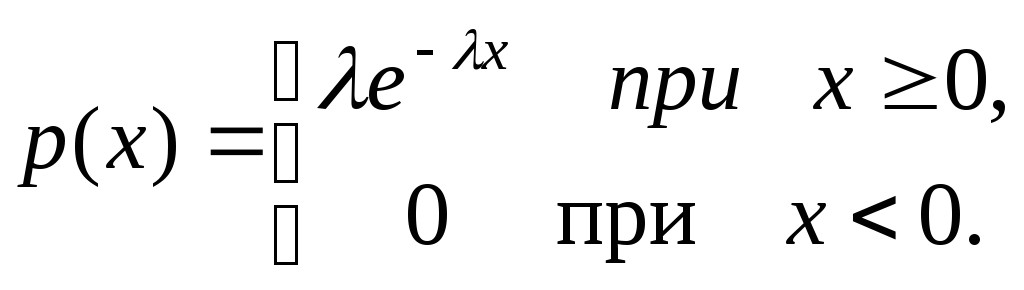
В дальнейшем показательное распределение будем обозначать E().
Из практики известно, что время безотказной работы телевизора распределено по показательному закону. Смысл параметра в том, что число 1/ равно среднему времени безотказной работы телевизора.
![]() .
.
Рисунок
3.4

Числовые
характеристики ДСВ.
Пусть дана ДСВ X
своим законом
распределения xi
pi.
Математическим
ожиданием ДВС X
называется число
![]() .
М.о. – сокращение словосочетания
“математическое ожидание”.
.
М.о. – сокращение словосочетания
“математическое ожидание”.
Смысл математического ожидания заключается в следующем: это вероятностное среднее значение случайной величины.
Дисперсией ДСВ X называется математическое ожидание квадрата отклонения ДСВ от ее математического ожидания:
![]()
Смысл дисперсии в том, что она является мерой рассеяния значений случайной величины от математического ожидания. Чем меньше дисперсия, тем меньше разброс значений от математического ожидания.
Сренеквадратическим
отклонением случайной
величины
Х
называется
число
![]() .
С.к.о.
– сокращение
словосочетания “Сренеквадратическое
отклонение”.
.
С.к.о.
– сокращение
словосочетания “Сренеквадратическое
отклонение”.
Эта величина более точно характеризует степень рассеяния значений случайной величины от математического ожидания, чем дисперсия. Обоснуйте почему?
Числовые характеристики непрерывных случайных величин. Пусть имеется НСВ X с плотностью распределения f(x).
Математическим
ожиданием НСВ X
называется число
![]() .
.
Дисперсией НСВ X называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
![]() .
.
Сренеквадратическим
отклонением случайной
величины
Х
называется
число
![]() .
.
Смыслы м.о., дисперсии, с.к.о. для НСВ те же, что и для ДСВ.
Лекция 4
4.1 Действия над случайными величинами
1. Сумма (разность) случайных величин. Пусть Х, Y – случайные величины с функциями распределения Fx(x) и Fy(y) соответственно. Суммой Z = X ± Y называется с.в. Z с функцией распределения Fz(z)=P(X±Y<z).
2. Произведением с.л. Х, Y называется с.в. Z= X Y с функцией распределения Fz(z)=P(XY<z).
3. Произведением числа С на с.в. Х называется с.в. Z = СХ с функцией распределения Fz(z) = P(СХ<z).
4.2 Независимые случайные величины. Пусть Х, Y – случайные величины с функциями распределения Fx(x) и Fy(y) соответственно. Функцией совместного распределения двух с.в. Х, Y называется функция от двух переменных
![]() .
.
Здесь под {X<x, Y<y} понимается произведение событий {X<x} и {Y<y}.
Плотностью совместного распределения непрерывных с.в. Х, Y называется функция
![]() .
.
С.в Х,
Y называются
независимыми,
если
![]()
![]() .
(4.1)
.
(4.1)
Из этого равенства
следует, что
![]() .
По определению условной вероятности
.
По определению условной вероятности
![]() .
.
Смысл этого равенства состоит в том, что независимость с.в. Х, Y означает, что закон распределения одной из них не изменяется от того, какое значение приняла другая в результате проведения опыта.
Если с.в. Х,
Y –
НСВ с плотностями
![]() соответственно, то их независимость
означает
соответственно, то их независимость
означает
![]()
![]() (4.2)
(4.2)
Для ДСВ Х, Y их независимость означает
![]()
![]() (4.3)
(4.3)
4.3 Свойства математического ожидания
Доказательства свойств проведем для ДСВ.
1. M[C]=C, где С=const. Действительно, P(X=C)=1. M[C]=C P(X=C)=C.
2. M[CX]=C×M[X], С – константа.
Закон распределения с.в. СХ имеет вид: С xi ® рi . Тогда
![]() .
.
3. M[X+Y]=M[X]+M[Y]. В частности, M[X+a]=M[X]+a, a=const.
Обозначим
![]() .Тогда
.Тогда
![]()
=![]()
В
предпоследнем равенстве воспользовались
свойством
![]() .
.
4. M[X]×M[Y] = M[X]×M[Y], если с.в. X,Y независимы.
Поскольку X,Y
независимы, то из (4.3) следует
![]() .
Тогда
.
Тогда
![]() .
.
5. Пусть с.в. Y является функцией j(X) от с.в. X. Тогда для верны формулы
![]() для ДСВ,
для ДСВ,
![]() для НСВ.
для НСВ.
Действительно,
закон распределения с.в. Y имеет вид
![]() .
Все равные значения
.
Все равные значения![]() заменяются одним, а соответствующие
вероятности складываются. Тогда по
определению м.о.
заменяются одним, а соответствующие
вероятности складываются. Тогда по
определению м.о.![]() .
.
Пример.
![]() для
ДСВ и
для
ДСВ и![]() для НСВ.
для НСВ.
