4.3.7 Разделенные разности

Рассмотрим случай, когда значение функции заданы в неравноотстающих узлах. При этом вместо конечных разностей рассматриваются разделенные разности, являющиеся в некотором смысле аналогом понятия производной и определяющиеся следующим образом.

Пусть функция y = f(x) задана своими значениями ,

, ,…, , … в узлахпроизвольной сетки.

Разделенные разности нулевого порядка совпадают со значениями функции в точках.Разделенными разностями первого порядка называются отношения

Разделенными разностями второго порядка называются отношения

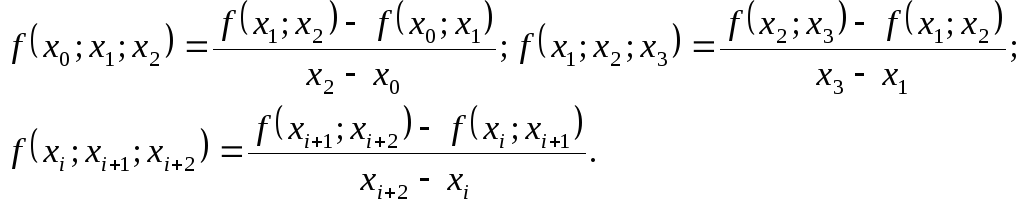
В общем случае разделенная разность k-го порядка определяется через разделенную разность(k-1)-го порядка по формуле

. (4.36)

Приведем некоторые свойства разделенных разностей

1. Разделенные разности всех порядков являются линейной комбинацией значений , а именно справедлива следующая формула:

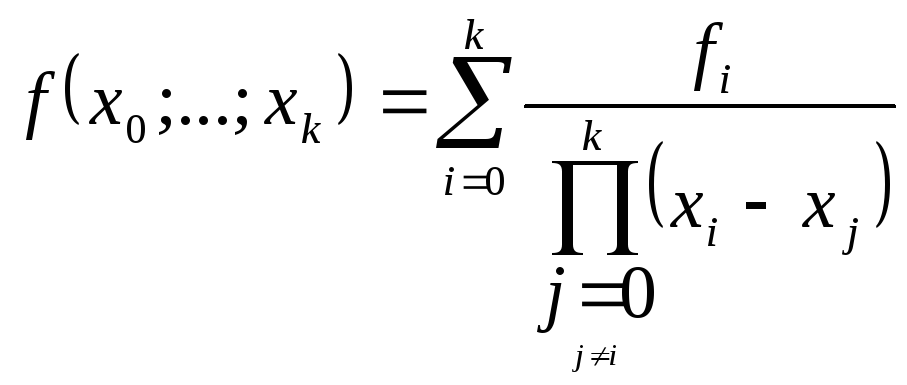. (4.37)

2. Разделенная разность есть симметрическая функция своих аргументов, т.е. не меняется при любой их перестановке.

3. Разделенная разность удовлетворяет равенству

, (4.38)

4. Если узлы принадлежат отрезкуи функцияf(x) имеет на непрерывную производнуюk-го порядка, то существует такая точка , что

. (4.39)

Из этого свойства вытекает простое следствие. Пусть

есть многочлен k-й степени. Тогда, очевидно, , и соотношение (4.39) дает для разделенной разности значение

Итак, у всякого многочлена k-й степени разделенные разности k – го порядка равны постоянной величине – коэффициенту при старшей степени многочлена. Разделенные разности высших порядков (больше k), очевидно, равны нулю.

4.3.8 Интерполяционный многочлен Ньютона для произвольной сетки узлов

Используя форму Лагранжа, представим интерполяционный многочлен в следующем виде:

Здесь ;; (k = 1,2,…n) – интерполяционные многочлены в форме Лагранжа, построенные по узлам .

Рассмотрим разности

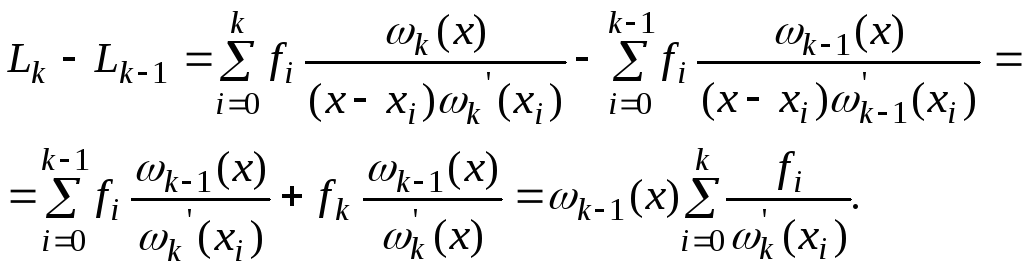
Таким образом, используя формулу (3.37), получим

(4.40)

а интерполяционный многочлен принимает форму

(4.41)

Эта форма называется интерполяционным многочленом Ньютона с раздельными разностями.

Выражение для погрешности имеет тот же вид, что и в случае многочлена Лагранжа [см.формулу(4.9)].

Отметим, что в формуле (4.41) интерполяционного многочлена на узлы накладывается единственное условие - их несовпадение. Поэтому нумерацию узлов можно произвести в произвольном порядке. Например, индексом «0» часто обозначают последующий узел таблицы, за принимают предпоследний узел и обозначают егои т.д. В этом случае многочлен (4.41) принимает форму

(4.42)

и ее называют многочленом Ньютона для интерполирования назад.

Сравнение форм Лагранжа и Ньютона интерполяционного многочлена позволяет рекомендовать использование представления в форме Лагранжа, во-первых, в теоретических исследованиях, например при изучении вопроса о сходимости к; во-вторых, при интерполировании нескольких функций на одной и той же сетке узлов, поскольку в этом случае можно один раз вычислить множители Лагранжа и использовать их для интерполяции всех функций.

Представление в форме Ньютона оказывается более удобным в практических расчетах. Действительно, число используемых узлов и степень интерполяционного многочлена часто заранее не известно, а при переходе от n узлов к (n+1)-му узлу в форме Ньютона добавляется лишь один член, имеющий смысл поправки к уже вычисленному значению. В то же время в форме Лагранжа добавление еще одного слагаемого сопровождается полным пересчетом полученного ранее результата. Кроме того, в вычислительной практике интерполяция обычно осуществляется на не большом отрезке длиной h<1. При этом слагаемые формы Ньютона имеет порядок ,…, т.е. расположены в порядке убывания, что оказывается полезным при определении точности результата интерполирования.