4.3.5 Интерполяционные многочлены Стирлинга и Бесселя

Рассмотрим задачу построения интерполяционного многочлена для функции f, заданной своими значениями иравномерной сетки с шагомh.

Пусть точка х* расположена вблизи некоторого узла, который обозначим . Требуется построить интерполяционный многочлен четной степени. В качестве узлов интерполирования следует выбрать сетку, симметричную относительно узла:

Введем новую переменную t, с помощью которой начало отсчета переводится в точку :

; (4.21)

при этом .

Используя средние арифметические соседних конечных разностей одного и того же порядка , можно получить интерполяционный многочлен Стирлинга, обычно обозначаемый:

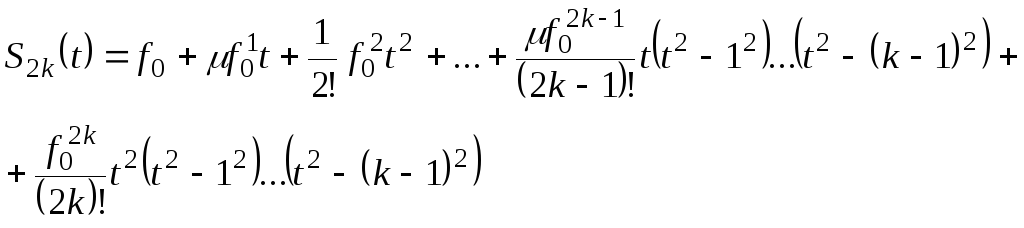(4.22)

Так как многочлен Стирлинга является лишь новой формой интерполяционного многочлена Лагранжа, построенного по узлам , то его остаточный член относительно переменнойt можно представить в виде

; , (4.23)

а оценку погрешности приближенного значения (погрешности метода) – в виде

, (4.24)

где .

Пусть теперь точка интерполирования лежит между узламиив близи точки. Требуется построить интерполяционный многочлен нечетной степени. Тогда сетка, минимизирующая погрешность, симметрична относительно точки, т.е. относительно точки.

На сетке можно получитьинтерполяционный многочлен Бесселя, обычно обозначаемый :

(4.25)

Так как многочлен Бесселя является еще одним представлением интерполяционного многочлена Лагранжа, построенный по узлам , то его остаточный член относительно переменнойt можно записать в виде:

, (4.26)

а оценку погрешности приближенного значения (погрешности метода) – в виде:

, (4.27)

где .

Итак, рассмотрено два интерполяционных многочлена: многочлен Стирлинга, который используется при построении многочлена четной степени и строится по нечетному числу узлов, и многочлен Бесселя, который используется при построении многочлена нечетной степени и строится по четному числу узлов.

Если же степень многочлена фиксирована не жестко, т.е. может быть как четной, так и нечетно, то целесообразно использовать многочлен Стирлинга в случае, когда

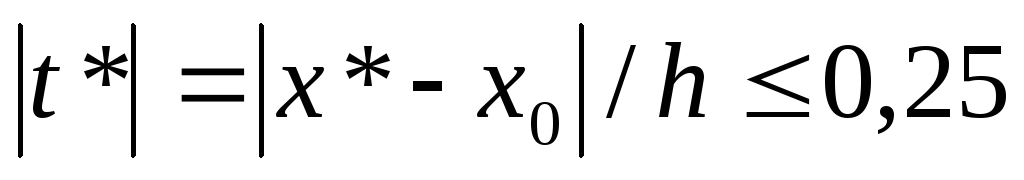, (4.28)

т.е. когда точка интерполирования расположена ближе к узлу, чем к середине между узлами. Многочлен Бесселя следует использовать в случае, когда

, (4.29)

т.е. когда точка интерполирования расположена ближе к середине между узламии. Одно из условий (4.28) или (4.29) всегда может быть обеспечено выбором соответствующего узла в качестве.

4.3.6 Интерполяционные многочлены Ньютона

Если точка интерполирования находится в начале или в конце таблицы, то не всегда возможно выбрать достаточное количество узлов слева и справа отдля построения необходимых конечных разностей. В этом случае используются специальные формы интерполяционного многочлена.

Пусть точка расположена в близи первого узла сетки. рассмотрим переменнуюt, определяемую соотношением (4.21), и построим интерполяционный многочлен.

Первый интерполяционный многочлен Ньютона обычно обозначается .

. (4.30)

Остаточный член относительно переменной t можно представить в виде:

; , (4.31)

а оценку погрешности приближенного значения (погрешности метода) – в виде:

, (4.32)

где .

Пусть точка расположена вблизи последнего узла сетки. Для этой сетки, снова используя переменнуюt, определяемую соотношением (4.21), построим интерполяционный многочлен.

Второй интерполяционный многочлен Ньютона обычно обозначается .

. (4.33)

с остаточным членом

, (4.34)

и оценкой погрешности приближенного значения

, (4.35)

где .

Формулы (4.30) и (4.33) часто называют соответственно интерполяционными формулами Ньютона для интерполирования вперед и назад.

Лекция № 12