
иНорматика el_polya
.pdf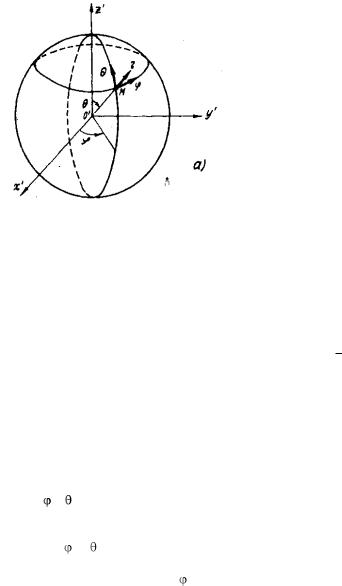
|
|
На рисунке 2.1 приведена |
||
|
|
сферическая |
система |
|
|
|
нат. Эта система формирует- |
||
|
|
ся тремя координатными по- |
||
|
|
верхностями, |
проходящими |
|
|
|
через интересующую |
нас |
|
|
|
точку М, и полярной осью |
||
|
|
О׳z׳, проходящей через нача- |
||
|
|
ло координат. Одна поверх- |
||
|
|
ность – сфера с центром в |
||
|
|
начале координат, вторая – |
||
|
|
|||
|
Рис. 2.1 |
плоскость, содержащая по- |
||
|
лярную ось и точку М, а тре- |
|||
|
|
|||
|
|
тья – плоскость, перпендику- |
||
|
|
|||
лярная полярной оси. Каждая пара координатных поверхностей, |
обра- |
|||
зует в пересечении координатную линию. Координатная линия может быть прямой или кривой. Система координат называется прямолинейной, если все координатные линия прямые. Если хотя бы одна коор-
динатная линия не прямая, система координат называется криволиней-
ной. Сферическая система координат – криволинейна.
Координатную систему называют ортогональной, если в любой точке Μ касательные к координатным линиям образуют прямоугольный трехгранник. Сферическая система координат ортогональна.
Если в точке Μ (рис. 2.1) задан некоторый вектор Е (например, вектор электрического поля). Его принято обозначать прямой со стрел-
кой, берущей начало в точке Μ. Не следует забывать, что этот вектор описывает, электрическое поле в точке Μ, а прямая со стрелкой
– лишь удобный способ графического отображения характеристик векторного поля в этой точке. Чтобы определить его проекции в нелинейной системе координат необходимо найти направление координатных осей в этой точке. Координатные оси всегда прямые. Они определяются как касательные к координатным линиям. На рис. 2.1 это прямые r , и .
Будем рассматривать однородную симметричную сферическую волну, у которой электрическое и магнитное поле не зависят от угловых координат и . Единственная координата, вдоль которой изменяется поле – радиус. Выберем систему координат так, чтобы электрическое поле было направлено по оси . Расчет показывает, что если на пути
41
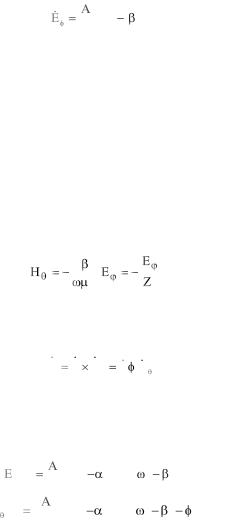
электромагнитной волны нет препятствий и, следовательно, не возникает отражений, то
|
exp( i r) , |
(2.26) |
r |
где А – амплитуда электрического поля в начале координат Ее значение зависит от условий возбуждения.
Если в плоской волне без потерь по мере распространения амплитуда поля не изменяется, то в сферической волне она уменьшается обратно пропорционально расстоянию от точки, в которой волна была возбуждена (от начала координат). Это объясняется довольно просто. Поверхность занятая плоской волной по мере распространения волны не изменяется, чего нельзя сказать о сферической волне. По мере распространения площадь поверхности, которую покрывает фронт сферической волны, увеличивается. Следовательно, на единицу площади приходится все меньше энергии и напряженность поля должна уменьшаться, что и следует из (2.26).
Воспользовавшись законом электромагнитной индукции, найдем магнитное поле.
|
|
|
|
|
|
|
|
. |
(2.27) |
||
|
|
|
|
||
ac
Усферических волн связь между электрическим и магнитным полем такая же, как и у плоских волн. Они связаны через волновое сопротивление среды. Магнитное поле перпендикулярно электрическому
инаправлению распространения. Вектор Пойнтинга
|
П |
|
E |
|
H |
* E H |
|
|
|
|
|
|
e |
(2.28) |
|||||
|
|
|
|
|
|
|
r |
||
|
|
|
|
|
|
|
|
||
направлен по радиусу.
Выражения (2.26), (2.27) описывают комплексное изображение электрического и магнитного поля в сферической волне. Запишем выражения для полей как функцию координат и времени, описывающую реальные поля, а не их изображения.
x (t) |
|
exp ( |
r) cos( |
t |
r); |
(2.29) |
|
|
|||||||
|
|
r |
|
|
|
||
|
|
|
|
|
|
||
H (t) |
|
|
exp ( |
r) cos( |
t |
r |
z ); |
r Zc (2.30)
Цилиндрические волны
42
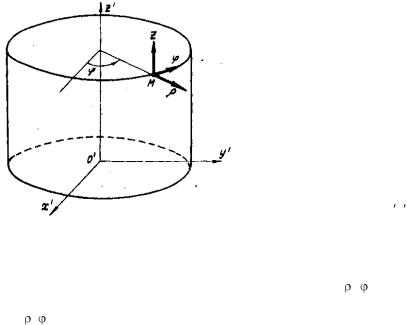
Цилиндрические волны радиально расходится от некоторой оси в пространстве, на которой расположен проводник с током. Структура цилиндрических волн существенно сложнее структуры плоских и сферических волн. Она требует введения цилиндрической системы координат (рис.
2.2)..
Система координат формируется тремя координатными поверхностями, проходящими через интересующую нас точку М, и полярной осью О׳z׳, проходящей через начало координат. Опишем эти поверхности. Одна поверхность – цилиндр, ось которого совпа-
Рис.2.2 |
дает с полярной осью О z ; |
|
вторая – плоскость, перпен- |
||
|
дикулярная полярной оси; а третья – плоскость, касательная к цилиндру и проходящая через точку М.
Каждая пара координатных поверхностей, образует в пересечении координатную линию. Цилиндрическая система координат , , z (см. рис. 2.2) – ортогональная и криволинейная. Координатные оси это прямые , , z (см. рис. 2.2).
Простейшая монохроматическая симметричная цилиндрическая волна с источником в центре удовлетворяет двумерному уравнению Гельмгольца и описывается с помощью первой функции Ханкеля нулевого порядка H0(x) , которая в свою очередь формируются из цилиндрических функций первого (J0(x)) и второго (Y0(x)) рода нулевого порядка.
Цилиндрические функции первого (J0(x) – функция Бесселя) и второго рода (Y0(x) – функция Неймана) – это хорошо изученные неэлементарные функции действительного аргумента, для которых существуют таблицы значений и которые, наряду с другими введены в основные математические программы, например, в MathCAD. На рис. 2.3 приводится графики этих функций.
В начале координат функция Бесселя J0(x) равна единице, а функция Неймана Y0(x) стремится к - ∞. Затем, по мере нарастания аргумента
43
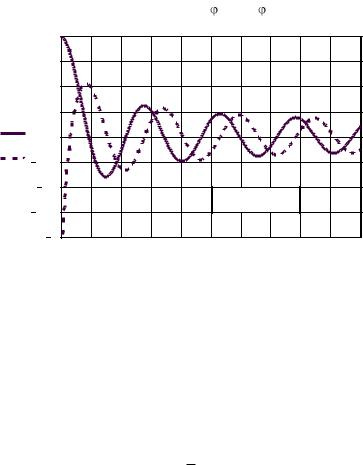
обе функции – изменяются и по величине и по знаку вблизи нуля и все больше приближаются к синусоиде. В цилиндрической системе координат эти функции выполняют ту же роль, что и функции синус и косинус в прямоугольной системе координат.
Кроме того, синус и косинус в прямоугольной системе координат используется записи комплексного числа в тригонометрической форме
z = a + bi = c(cos |
+ i sin |
). |
Аналогично цилиндрические функции |
первого |
и второго рода тоже |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
0.75 |
|
|
|
|
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
J0(x) |
0.25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y0(x) |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.25 |
|
|
|
|
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.2.3 |
|
|
|
|
|
0.75 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
2.5 |
5 |
7.5 |
10 |
12.5 |
15 |
17.5 |
20 |
22.5 |
25 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
можно использовать |
для записи комплексных чисел в цилиндрической |
|||||||||||
системе координат. |
|
|
|
|
|
|
|
|
|
|
||
H0 (x) = J0 (x) + i N0 (x);
Это и есть функция Ханкеля нулевого порядка, которая используется для описания цилиндрических волн. На рис. 2.4 приводится график модуля функции Ханкеля. Модуль функции, определяет амплитуду цилиндрической волны и уменьшается по мере увеличения ее аргумента. Следовательно, по мере распространения амплитуда цилиндрической волны будет уменьшаться.
На рис.2.4 сплошной линией построен график модуля функции Хан-
келя, а пунктиром – функция A1/ 
 x , где А1 подобрана так, чтобы при x = 25 значение функции совпадало с функцией Ханкеля. Графики
x , где А1 подобрана так, чтобы при x = 25 значение функции совпадало с функцией Ханкеля. Графики
44
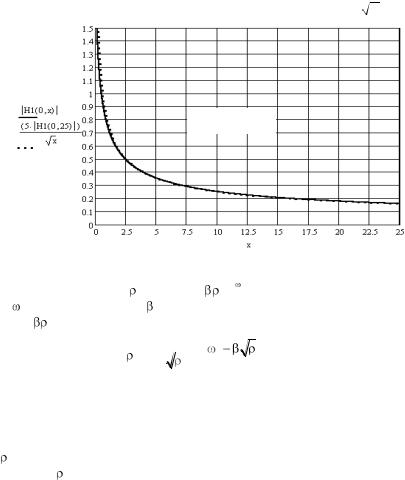
практически полностью повторяют друг друга и лишь слегка расходятся при малом значении аргумента.
Таким образом, в практических приложениях для расчета электрического поля цилиндрической волны можно пользоваться упрощенным
выражением, использующим вместо функции Ханкеля функцию 
 x .
x .
Рис.2.4
Электрическое поле в цилиндрической волне с помощью функции
Ханкеля записывается так: |
|
|
|
|
|
|
|
|
|
E( , t) = Re{H0( |
) ei |
t}, |
(2.31) |
||||||
где – круговая частота, а |
– волновое число. На больших расстояниях |
||||||||
от оси ( >> 1) волновое поле приобретает вид: |
|
||||||||
|
|
A |
|
|
|
|
|
|
|
E( , t)= |
|
cos( |
t |
) |
|
||||
|
|
|
|
||||||
|
|
|
|
. |
(2.32) |
||||
Только в этом асимптотическом представлении в цилиндрической волне можно однозначно выделить амплитуду и фазу. В этом приближении фазовая скорость цилиндрической волны совпадает с фазовой скоростью плоской волны.
По мере удаления от оси квадрат модуля амплитуды убывает как 1/ , а поверхность цилиндра, охватывающая источник, растѐт пропорционально , так что, в соответствии с законом сохранения энергии, суммарное значение потока энергии, уносимого от источника на оси, остаѐтся постоянным. Электромагнитную волну приближенно можно рассматривать как плоскую с медленно изменяющейся амплитудой. То-
45

гда магнитное поле в волне можно найти, воспользовавшись волновым сопротивлением среды, как это и делалось для плоской волны.
Лабораторная работа 5. Электромагнитные волны.
Цель работы: Изучить методы описания плоских, сферических и цилиндрических волн. Научиться рассчитывать параметры плоских волн в различных условиях.
Используемое программное обеспечение: MathCAD, версия не ниже MathCAD13/
Лабораторное задание
1.Составьте программу для MathCAD по расчету параметров
плоской волны, распространяющейся в среде с =1, = 1, магнитная проводимость среды σм равна нулю, а электрическая проводимость σе задается номером варианта, умноженным на 10-4 Сименс. Амплитуда электрического поля (E0) – номер варианта. Частота сигнала – номер варианта, умноженный на 108 Герц. Нужно составить программу для расчета постоянной распространения, волнового числа, постоянной затухания, волнового сопротивления, показателя преломления и фазовой скорости плоской волны.
2.Создайте два линейных графика зависимости электрического поля в плоской волне от времени в точке z = 0 и в той точке,
координата z которой /2 . На графике должно расположиться 3 – 5 периодов колебаний. Чем отличаются графики и почему? Обсудите полученный результат.
3.При t = 0 постройте два графика: зависимость от продольной координаты электрического поля в плоской волне и зависимость от продольной координаты магнитного поля. По продольной оси отложите столько колебаний, чтобы было видно затухание сигнала по мере его распространения Каковы особенности этих графиков? Обсудите полученный результат.
4.Постройте два графика: зависимости средней активной и средней реактивной мощности от продольной координаты. Обсудите полученный результат.
5.Постройте на одном графике распределение электрического поля вдоль продольной оси для плоской, цилиндрической и сфе-
рической волны при отсутствии затухания ( = 0). Начало гра-
46

фика выберите так, чтобы для цилиндрической волны выполнялось условие z >>1 и, следовательно, для нее можно будет говорить об амплитуде и фазе волны и справедливо выражение (2.32). Например, график можно начинать со значения продольной координаты u0 = 15/ .
Методические указания к выполнению лабораторного задания
Лабораторное задание выполняется по вариантам. Параметры среды и сигнала описаны в задании на лабораторную работу.
Введем обозначения для переменных и функций.
f– частота
–относительная диэлектрическая проницаемость,
– относительная магнитная проницаемость σe – электрическая проводимость,
σm – магнитная проводимость,
0 – магнитная проницаемость вакуума,
0 – диэлектрическая проницаемость вакуума
– круговая частота,
n – комплексная диэлектрическая проницаемость, n – комплексная магнитная проницаемость,
n – показатель преломления c – скорость света в вакууме
zc0 – волновое сопротивление вакуума
–постоянная распространения,
–волновое число или фазовая постоянная,
–постоянная затухания,
zc – волновое сопротивление среды,
– длина волны,
vf – фазовая скорость плоской волны t - текущее время;
z – текущая координата вдоль оси, по которой распространяется электромагнитное поле;
EK(z) – комплексная амплитуда электрического поля плоской вол-
ны;
EK1(z) – комплексная амплитуда электрического поля плоской волны в среде без потерь;
EKС(z) – комплексная амплитуда электрического поля цилиндрической волны в среде без потерь;
47
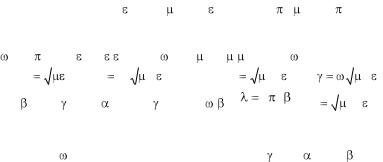
EKS(z) – комплексная амплитуда электрического поля сферической волны в среде без потерь;
НK(z) – комплексная амплитуда магнитного поля плоской волны; НK1(z) – комплексная амплитуда магнитного поля плоской волны,
комплексно сопряженной волне НK(z);
E(z,t) – мгновенное значение электрического поля плоской волны в точке с продольной координатой z в момент времени t;
E1(z,t) – мгновенное значение электрического поля плоской волны, у которой отсутствует затухание, в точке с продольной координатой z, в момент времени t;
EС(z,t) – мгновенное значение электрического поля цилиндрической волны, у которой отсутствует затухание, в точке с продольной координатой z, в момент времени t;
ES(z,t) – мгновенное значение электрического поля сферической волны, у которой отсутствует затухание, в точке с продольной координатой z, в момент времени t;
H(z,t) – мгновенное значение магнитного поля в точке с продольной координатой z в момент времени t;
PSR(z) – Плотность потока активной мощности вдоль оси z; QSR(z) – Плотность потока реактивной мощности вдоль оси z.
Алгоритм расчета.
1. При составлении программы для расчета параметров плоской волны сначала введите заголовок «Исходные данные», а затем сами исходные данные:
f := |
E0 := |
:= 1 |
:= 1 0 := 10-9/36 |
0 := 4 107 |
σe := |
σm := 0 |
|
|
|
Введите заголовок «Формулы для расчета», а затем сами формулы:
:= 2 f |
|
|
n := |
0 – i σe/ |
n := |
0 – i σm/ |
|
|
|
|
||
|
|
|
|
|
|
zc0 |
|
0 / 0 |
|
|
n n |
|
n |
|
|
с |
1/ 0 0 |
|
|
||||||
|
|
|
|
|
|
|
2 / |
|
|
|
|
|
= Re( ) |
|
= – Im( ) |
vf = / |
zc |
n / n |
|||||||
|
|
|
||||||||||
Введите заголовок «Результаты расчета», а затем запросите ре-
зультаты: = n = c = vf = zc0 = zc = = = =.
Программа для расчета параметров создана и получены результаты расчетов.
48

2. Графики нужно построить для функций, описывающих электромагнитное поле. Для всех типов волн переменная для координаты будет обозначаться u. Это необходимо для того, чтобы выполнить пятый пункт задания. Для плоских волн u подставляется вместо z, для цилиндрических вместо , а для сферических вместо r.
Введите заголовок «Формулы для построения графиков для плоской волны», а ниже введите сами формулы расчета величин, для которых будут строиться графики (обозначение переменных проведено немного
выше) |
|
|
|
|
|
|
|
|
|
|
EK(u):=E0 e-i u |
HK(u) := EK(u)/zc |
HK1(u) = Re(HK(u)) – i Im(HK(u)) |
||||||||
E(u,t):= Re (EK(u) ei |
t) |
|
H(u,t):= Re (H(u) ei t) |
|||||||
PSR(u):= 0.5*Re (EK(u) HK1(u)) |
QSR(u):=0.5* Im (EK(u) HK1(u)) |
|||||||||
Теперь введите диапазон, и шаг изменения времени и координаты |
||||||||||
t 0 |
0.001 20 |
u |
0 |
0.001 100 |
||||||
|
|
|
|
|
|
|
|
|||
Все готово для выполнения пунктов 2, 3, 4 задания. Используйте X- Y-графики для выполнения этих пунктов задания. При построении графиков зависимости электрического и магнитного поля в плоской волне от продольной координаты воспользуйтесь выражениями для E(u,t) и H(u,t) при t = 0. . Неплохие результаты получаются, если отобразить 15
– 20 периодов колебаний. Впрочем, это зависит от параметра затухания, заданного в варианте задания. Обсудите полученный результат. Чем определяется период, амплитуда и затухание полученного сигнала? Попробуйте поварьировать те параметры, от которых, по вашему мнению, эти величины зависят, и посмотрите, к каким изменениям на графике это приводит. Сделайте выводы.
Чтобы выполнить пятый пункт задания запишите выражения для электрического поля в цилиндрической и сферической системах координат. Потери отсутствуют и вместо постоянной распространения γ нужно использовать волновое число β.
|
|
|
|
EKS(u) := (E0 e-i u )/u |
EKC(u) := (E0 e-i u )/ u |
||
ES(u,t) := Re (EKS(u) ei t) |
EC(u,t) := Re (EKC(u) ei t) |
||
3. При построении графиков зависимости электрического поля в |
|||
плоской, цилиндрической и сферической волне при отсутствии затухания от продольной координаты воспользуйтесь выражениями для E(u,t) и EC(u,t) ES(u,t) при t = 0. В этих выражениях вместо постоянной распространения  стоит волновое число и затухание отсутствует. Непло-
стоит волновое число и затухание отсутствует. Непло-
49

хие результаты получаются, если отобразить электрическое поле при изменении продольной координаты от 15/ метров до 75/ метров.
Содержание отчета
Отчет должен содержать название работы, цель, краткие выводы из теории (не обязательно), результаты выполнения лабораторного задания по пунктам, и выводы по работе.
Описывая результаты выполнения очередного пункта лабораторного задания необходимо указать:
заголовок, условие задачи,
решение поставленной задачи в MathCad, обсуждение полученных результатов.
Выводы по работе должны отображать достижение цели лабораторной работы и обсуждение всей работы в целом.
Контрольные вопросы
1.Запишите выражение для комплексной амплитуды электрического поля в плоской волне и выражение для электрического поля как функции координат и времени. Дайте определения для всех параметров в этих выражениях.
2.Как рассчитать магнитное поле в плоской волне, если известно электрическое? В каком случае волновое сопротивление среды будет действительным и комплексным. Как это отражается на магнитном поле, если электрическое задано.
3.Что такое постоянная распространения и как она рассчитывается. Опишите ее действительную и мнимую часть.
4.Что такое фаза электромагнитной волны, как она рассчитывается. Дайте определения для всех параметров в выражении для расчета фазы.
5.Что такое групповая и фазовая скорость плоской волны. Как они рассчитываются в среде с отличной от 0 диэлектрической проницаемостью. Дайте определения для всех параметров в выражении для расчета скоростей.
6.Как рассчитать и среднюю активную и среднюю реактивную мощность плоской волны?
7.Запишите выражение для комплексной амплитуды электрического поля в сферической волне, и выражение для электрического поля как функции координат и времени. Дайте определения для всех параметров в этих выражениях.
8.Запишите выражение для комплексной амплитуды электрического поля в цилиндрической волне, и выражение для электрического поля как функции координат и времени. Дайте определения для всех параметров в этих выражениях
9.Опишите функции Бесселя и Неймана.
10.Опишите функции Ханкеля.
50
