иНорматика el_polya

6.Сформулируйте и поясните второе уравнение Максвелла в дифференциальной форме для вакуума и для вещества.

7.Сформулируйте и поясните второе уравнение Максвелла в интегральной форме для вакуума и для вещества.

8.Переведите второе уравнение Максвелла в дифференциальном виде для вакуума и для вещества в комплексную форму.

9.Переведите второе уравнение Максвелла в интегральном виде для вакуума и для вещества в комплексную форму.

10.Как рассчитать магнитное поле от дискретного набора зарядов и от заряда, распределенного в некоторой области.

Лабораторная работа 4. Расчет переменного магнитного поля и электромагнитной индукции

Цель работы: Научиться рассчитывать величину электродвижущей силы, созданной переменным магнитным полем в контуре.

Используемое программное обеспечение: MathCAD, версия не ниже версии MathCAD 13; программа для MathCAD, составленная при выполнении предыдущей лабораторной работы.

Лабораторное задание

1.Модернизировать программу для расчета магнитной индукции, созданную в предыдущей лабораторной работе так, чтобы можно было рассчитать магнитную индукцию от набора перемен-

ных токов. Частота сигналов задается номером варианта,

умноженным на 105Гц. Расчет провести методом комплексных амплитуд. Комплексные амплитуды токов в проводниках заданы в шестом столбце таблицы 1.2. Используется и действи-

тельная и мнимая части комплексной амплитуды.

2.Рассчитать магнитную индукцию в 2500 точках, расположен-

ных равномерно в квадрате с координатами (смотри таблицу

1.3) (x1, y1), (x1, y2), (x2, y1), (x2,y2). Координаты z и в этой таблице не используются.

3. Найти ЭДС, возникающую в контуре. Рассчитать ее модуль и фазу и построить зависимость ЭДС в контуре от времени в течение 3 – 5 периодов.

Методические указания к выполнению лабораторного задания

Лабораторное задание выполняется по вариантам. В таблицах1.2 и 1.3 приведены исходные данные. Для каждого варианта задается 4 про-

31

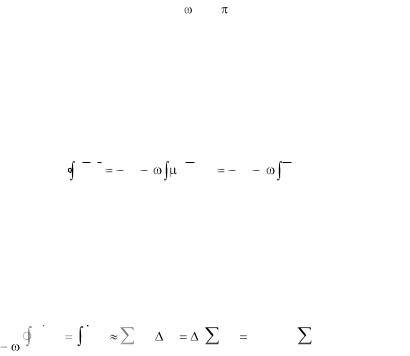
водника с током. Начало проводников – точки с координатами x1 и y1, а конец точки с координатами x2 и y2. Комплексная амплитуда тока в проводнике величина, взятая из шестого столбца. Частота сигналов задается номером варианта, умноженным на 105Гц.

Координаты точек вершин квадрата, в котором нужно было рассчитать магнитную индукцию в предыдущей лабораторной работе, теперь представляют собой вершины квадратного витка, в котором нужно найти ЭДС.

Расчет будем проводить методом комплексных амплитуд. Скопируем программу для расчета магнитного поля LabEMP3_1.mcd и сохраним ее под именем LabEMP4.mcd. В дальнейшем мы будем модернизировать эту программу с целью выполнения задания для лабораторной работы 4.

1. Введем дополнительные исходные данные для этой лабораторной работы

f := := 2* *f

2. Исправим значения тока в исходной матрице. Теперь для тока нужно использовать комплексные значения, заданные в столбце q таб-

лицы 1.2. Введите эти данные. Удалите выражение для расчета BIIix,iy - магнитной индукции от тока конкретного проводника и оба графика.

Проведите расчет. Если все работает правильно, то будет рассчитываться комплексная амплитуда магнитного поля в интересующем нас участке пространства.

3. Дальнейший расчет связан с вычислением электродвижущей силы. Ее будем рассчитывать, воспользовавшись выражением (1.33)

В левой части равенства стоит выражение, которое и определяет электродвижущую силу. Первое слагаемое в правой части – магнитный ток. В условии задачи он отсутствует, следовательно этот ток равен нулю. Второе слагаемое должно быть использовано для расчета. В интересующей нас области в (ixm*iym) числе точек подсчитана магнитная индукция. Эти значения можно использовать для расчета интеграла. Интеграл считается по поверхности прямоугольника площадью x1*y1. Заменим интеграл суммой.

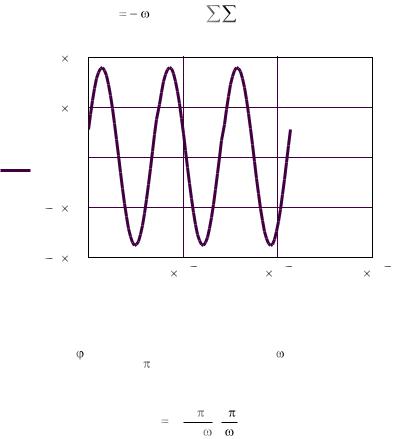
Прямоугольник разделен на (ixm*iym) прямоугольников одинакового размера (x1*y1)/ (ixm*iym). В пределах каждого прямоугольника поле считается постоянным. Тогда для расчета ЭДС нужно ввести выражение:

1 104

5 103

ET ( t) 0

t

4. Рассчитаем модуль и фазу ЭДС в комплексной форме и запишем выражения для расчета ЭДС во временной области:

5. Построим зависимость ЭДС от времени. Для этого зададим промежуток времени, в течение которого будет строиться график:

t : 0,1006 .. 6

и построим график функции ET(t). На рисунке ниже приводится график зависимости ЭДС от времени для варианта 28.

33

Содержание отчета

Отчет должен содержать название работы, цель, краткие выводы из теории (не обязательно), результаты выполнения лабораторного задания по пунктам, и выводы по работе.

Описывая результаты выполнения очередного пункта лабораторного задания необходимо указать:

заголовок, условие задачи,

решение поставленной задачи в MathCad, обсуждение полученных результатов.

Выводы по работе должны отображать достижение цели лабораторной работы и обсуждение всей работы в целом.

Контрольные вопросы

1.Сформулируйте и поясните закон электромагнитной индукции в дифференциальной форме для вакуума и для вещества.

2.Сформулируйте и поясните закон электромагнитной индукции в интегральной форме для вакуума и для вещества.

3.Переведите закон электромагнитной индукции в дифференциальном виде для вакуума и для вещества в комплексную форму.

4.Переведите закон электромагнитной индукции в интегральном виде для вакуума и для вещества в комплексную форму.

5.Сформулируйте и поясните закон полного тока в интегральной форме для вакуума и для вещества.

6.Переведите закон полного тока в дифференциальном виде для вакуума и для вещества в комплексную форму.

7.Переведите закон полного тока в интегральном виде для вакуума и для вещества в комплексную форму.

8.В чем состоит принцип перестановочной двойственности? Используйте его для записи уравнений Максвелла в вакууме в дифференциальной форме.

9.Какова структура полного тока? Что такое ток проводимости и ток смещения.

10.Как рассчитать ЭДС самоиндукции в переменном магнитном поле?

2. Электромагнитные волны

Электромагнитные волны получают, как результат решения однородных уравнений Гельмгольца, которые непосредственно вытекают из уравнений Максвелла.

Уравнения Гельмгольца

34

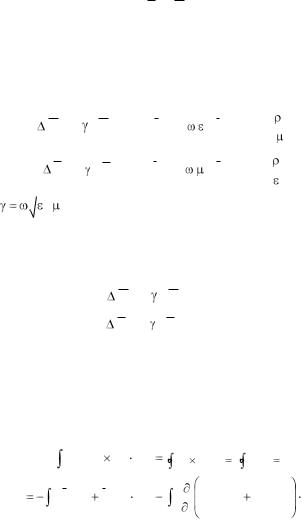
Вторую пару уравнений Максвелла не всегда удобно использовать

из-за того, что в оба вектора E и H входят и в первое, и во второе уравнение пары. Обычно эти уравнения преобразуют так, чтобы вектора разделились. Это преобразование можно проделать во временной области и для комплексных амплитуд. В первом случае уравнения называют волновыми, а во втором – уравнениями Гельмгольца. При анализе электромагнитных процессов в технических средах применяется уравнения Гельмгольца.

поля.

Это дифференциальные уравнения второго порядка с ненулевой правой частью. В таком виде уравнения Гельмгольца используются редко. Чаще используют однородные уравнения.

Плотность потока мощности электромагнитного поля. Вектор Пойнтинга

Электромагнитное поле способно накапливать и переносить энергию. Законы изменения, сохранения и распространения энергии можно получить из уравнений Максвелла.

Для конечного объема V несложно получить такое соотношение:

которое называют теоремой Пойнтинга в среде без потерь. Теорема Пойнтинга это форма закона сохранения энергии для электромагнитного поля.

35

Рассмотрим сначала нижнюю строчку выражения. Первый интеграл

– мощность электромагнитного поля связанная с протеканием электрического и магнитного тока, Второй интеграл – мощность, накопленная в электрическом и магнитном поле.

Итак, нижняя строка описывает полную мощность, накопленную в электромагнитном поле с учетом мощностей электрического и магнитного тока. Если эта величина изменяется, то появляется поток вектора

П E H (2.6)

через поверхность S, ограничивающую объем V. Источник вектора Пойнтинга (см. первый интеграл в верхней строке выражения (2.5)) – изменение мощности токов, протекающих в поле (первый интеграл в нижней части выражения (2.5)) или изменение энергии самого поля в объеме V (второй интеграл там же).

Мощность запасенная в электромагнитном поле изменяется за счет потока мощности через ограничивающую объем поверхность.

Вектор Пойнтинга можно ввести и для комплексных амплитуд. В этом случае

Плоские электромагнитные волны

Электромагнитную волну называют плоской, если и электрическое, и магнитное поле не изменяется в плоскости перпендикулярной направлению ее распространения. Плоская волна – это наиболее часто используемая модель электромагнитного волнового процесса в открытом пространстве. Выражение для плоской волны удобно искать в прямоугольной системе координат (х, у, z).

Пусть плоская волна распространяется вдоль оси z, то есть вектор Пойнтинга имеет единственную проекцию Пz, которую можно найти, спроектировав выражение (2.6) на ось z.

Отсюда следует, что в плоской волне отличны от нуля только поперечные составляющие электромагнитного поля. Электромагнитное поле поперечное.

36

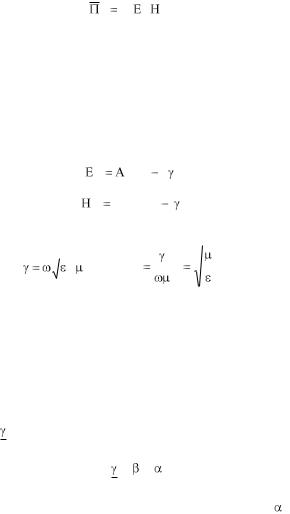
В плоскости перпендикулярной направлению распространения (плоскость xoy) координатные оси пока можно расположить произвольно. Направим ось x по электрическому полю, тогда Ey = 0. Теперь, в выражении (2.8) останется одно слагаемое,

Таким образом, плоскую волну можно представить в виде электромагнитного поля, содержащего одну проекцию электрического поля (Ex) и одну проекцию магнитного поля Hy.

Изменение этих проекций во времени и пространстве можно получить, решая уравнение Гельмгольца для электрического поля в прямоугольной системе координат и рассчитывая магнитное поле с помощью уравнения электромагнитной индукции. Для комплексных амплитуд полей, при условии, что на пути распространения радиоволн нет никаких препятствий и поэтому отраженной волны нет, получим:

Величину ZC называют волновым сопротивлением среды. Волно-

вое сопротивление позволяет рассчитать магнитное поле в плоской волне, если известно электрическое. В общем случае волновое сопротивление – величина комплексная. Его мнимая часть определяется электрической и магнитной проводимостью среды. В среде без потерь мнимая часть волнового сопротивления равна нулю и электрическое и магнитное поле в пространстве взаимно перпендикулярны.

В выражения (2.10, 2.11) входит комплексная постоянная распространения . Ее действительная и мнимая часть по-разному влияют на

Действительную часть постоянной распространения 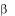называют

волновым числом или фазовой постоянной, а мнимую – постоян-

ной затухания. Воспользовавшись новой формой постоянной распро-

37

странения, перепишем выражения для комплексных амплитуд электрического и магнитного поля в плоской волне

образовать в функцию координат и времени, описывающую реальные поля, а не их изображения. Для этого каждое изображение нужно умножить на мгновенный комплекс (exp(i t)) и от полученного произведения взять действительную часть. Проделаем это и получим:

его фаза.

Итак, получены выражения для комплексного изображения электрического и магнитного поля в плоской волне (2.14) и (2.15) и выражения для расчета значения самого электрического и магнитного поля (2.16) и

(2.17).

Ввиду большой значимости этих выражений, обсудим полученный результат. Начнем с выражения (2.16) для электрического поля.

Выражение содержит периодическую функцию – косинус. Аргумент косинуса непрерывно изменяется в пространстве и во времени. Его на-

зывают фазой электрического поля плоской волны Ф,

ФЕ = t - z. (2.18)

Фаза магнитного поля отличается на фазовый угол волнового сопротивления,

ФН = t - z - z.

Косинус периодическая функция, поэтому через 2 радиан значения полей повторяются. Если зафиксировать координату и изменять время, то значения поля повторяются через

Это значение называют периодом по времени, или просто периодом. Если же сделать мгновенную фотографию, то есть зафиксировать время и смотреть, как изменяются поля с изменением координат, то несложно установить, что значения поля повторяются через

38

Это значение называют периодом по координате, или длиной вол-

ны.

Из (2.18) видно, что фаза плоской волны в плоскости перпендикулярной оси z постоянна. Это и есть основное свойство плоской волны. Уравнение поверхности постоянной фазы - плоскость перпендикуляр-

Каждая величина, входящая в выражение для фазы (2.18) имеет свое название. Кроме переменных координаты z и времени t в выражение входит круговая частота и волновое число .

Выражение, которое стоит перед функцией косинуса в (2.16) назы-

вают амплитудой электрического поля в плоской волне, та же величина в (2.17) – амплитуда магнитного поля плоской волны.

Отношение амплитуды электрического поля к амплитуде магнитного поля – волновое сопротивление. Волновое сопротивление определяется только параметрами среды и не зависит от величины электрического и магнитного поля (нелинейные среды мы пока не рассматриваем). Обе амплитуды уменьшаются при увеличении координаты z с постоянной затухания .

Плоская монохроматическая волна - это идеализация реального электромагнитного процесса. Известно, что информация передается модулированным колебанием, которое, как правило, имеет узкий спектр, располагающийся вблизи некоторой центральной частоты. Такой сигнал можно заменить монохроматической плоской волной, амплитуда которой изменяется по определенному закону. Скорость перемещения максимума амплитуды этой волны и называют групповой скоростью.

Возьмем узкополосный немонохроматический сигнал Ε (t). Используя преобразование Фурье, его можно представить в виде конечного или

Сигнал считаем узкополосным, то есть Δωmax/ω 0 << 1, где Δωmax - максимальное отклонение по круговой частоте от центральной ω0. Воспользуемся этим свойством сигнала для того, чтобы представить его в

39

виде гармонического колебания с несущей круговой частотой ω0. Для этого волновое число β разложим в степенной ряд вблизи несущей. Учитывая то, что отклонение частоты от центральной невелико, в ряду удержим лишь первые два слагаемые

Волновое число узкополосного немонохроматического сигнала представлено в виде двух слагаемых. Первое слагаемое – волновое число монохроматической несущей. Второе слагаемое возникает из-за того, что существуют спектральные составляющие с частотой, отличной от несущей. Их распространение описывается с помощью понятия групповой скорости.

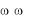
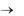d 0

Перепишем экспоненту в выражении (2.22) с учетом введенных обозначений.

Само выражение (2.22), теперь запишется так:

Узкополосный немонохроматический сигнал (2.22) заменен эквивалентным монохроматическим (см. выражение 2.25) с круговой частотой 0 и волновым числом 0 – соответствующим центральной частоте немонохроматического сигнала и амплитудой, определяемой выражением (2.25) перед мнимой экспонентой. Этот сигнал перемещается во време-

ни со скоростью vГР.

Сферические волны

Сферическую волну можно получить от – точечного источника. Если среда однородна во всех направлениях, то фаза волны постоянна на поверхности сферы. Это и будет сферическая волна. Задача по расчету электромагнитного поля в этом случае имеет сферическую симметрию. Ее следует решать в сферической системе координат.

40