иНорматика el_polya

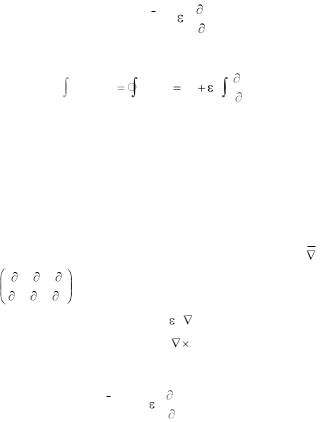
щью закона полного тока, который еще называют третьим уравнением Максвелла. Для точки используют дифференциальную форму закона:

а для поля от тока, распределенного по некоторой площади S, ограниченной кривой L используют интегральную форму закона.

Эти соотношения выглядят несколько сложнее выражений для расчета электрического поля (1.7) и (1.8). Это связано с двумя причинами.

Во-первых, в левой части уравнения (1.19) стоит операция нахождения ротора, а эта операция сложнее операции расчета дивергенции (см.1.7). Магнитное поле направлено перпендикулярно к току и направлению от точки, в которой проводится расчет. Плотность тока не является источником расходящегося из этой точки магнитного поля, а определяет вращательную его составляющую. Эта операция ближе к векторному произведению, а не скалярному. Действительно, если в

прямоугольной системе координат ввести фиктивный вектор с про-

Во-вторых, в уравнении (1.19) в правой части кроме плотности то-

Из структуры выражения (1.20) следует считать эту величину еще одним видом тока. Ее называют током смещения. Таким, образом, магнитное поле создается ток проводимости (1.12) или током смеще-

ния (1.21).

Процесс возникновения магнитного поля от второго слагаемого в правой части выражения (1.19) можно рассмотреть и по-другому. Магнитное поле возникает тогда, когда есть ток или изменяющееся электрическое поле. Изменяющееся электрическое поле создает перемен-

11

ное магнитное поле. Такой процесс можно назвать индукцией. Впрочем, электромагнитной индукцией принято называть обратный процесс – возникновение электрического поля при изменении магнитного.

Выражения для расчета магнитного поля (1.19) и (1.20) можно записать для переменных токов, изменяющихся с определенной круговой частотой , воспользовавшись методом комплексных амплитуд.

S

Принцип перестановочной двойственности

Мы получили два уравнения Максвелла, позволяющие рассчитать электрическое поле, создаваемое электрическим зарядом и магнитное поле, создаваемое электрическими токами проводимости и смещения. Существует еще два уравнения Максвелла, второе и четвертое. Чтобы записать эти уравнения предполагают, что электрические и магнитные явления однотипны. Наряду с электрическими зарядами и токами вводятся магнитные заряды qm и плотность магнитных токов проводимо-

магнитное поле, а магнитные токи – кольцевое электрическое поле. Поля, создаваемые этими объектами можно получить, если в уже рассмотренных уравнениях Максвелла провести замену:

В этом и состоит принцип перестановочной двойственности, анало-

гичный принципу дуальности электрических цепей с реактивными элементами. Более того, такие замены можно проводить в результатах расчета полей. Это значительно упрощает расчеты электромагнитных полей.

Закон непрерывности магнитных силовых линий (второе уравнение Максвелла)

Применим принцип перестановочной двойственности к первому уравнению Максвелла и запишем закон непрерывности магнитных силовых линий последовательно в дифференциальной (1.25), инте-

12

гральной (1.26) форме и для комплексной амплитуды напряженности полей (1.27), (1.28).

Здесь введена комплексная магнитная проницаемость, которая получается из (1.11)

Закон электромагнитной индукции ( четвертое уравнение Максвелла)

Применим принцип перестановочной двойственности к третьему уравнению Максвелла и запишем закон электромагнитной индукции последовательно в дифференциальной (1.30), интегральной (1.31) форме и для комплексной амплитуды напряженности полей (1.32), (1.33).

S

В таблицу 1 сведены все расчетные формулы, позволяющие рассчитать электромагнитное поле при произвольном распределении токов и зарядов. Для расчета полей от точечных зарядов и дискретных проводников с током используют выражения (1.2) и выражение (1.17). В последнем случае считают проводники бесконечно длинными.

13

Лабораторная работа 2. Расчет электрического поля от дискретного набора электрических зарядов

Цель работы: Научиться рассчитывать напряженность электрического поля от произвольного набора электрических зарядов в произвольной точке трехмерного пространства.

Используемое программное обеспечение: MathCAD, версия не ниже MathCAD13.

Лабораторное задание

1.Освоить методику составления программы для расчета электрического поля от набора точечных источников.

2.Составить программу расчета электрического поля в наборе точек трехмерного пространства, для которого = 1. Поле созда-

ется набором точечных зарядов (до 10 штук, в задании даются значения в 4 точках, см. табл.1.2). Заряд, величина которого задана в кулонах*10-9, располагается в точке с координатами (х1, y1, z1).

Рассчитать электрическое поле в 10 точках, равномерно распределенных на заданном отрезке прямой, начало и конец которой заданы в табл.1.3. Рассчитывается модуль вектора электрического поля, его проекции на координатные оси. В отчете привести график изменения электрического поля и его проекций на координатные оси.

Методические указания к выполнению лабораторного задания

Лабораторное задание выполняется по вариантам. В таблицах 1.2 и 1.3 приведены исходные данные. В каждом варианте задается 4 заряда. Для каждого заряда указано его положение – координаты в прямоугольной системе координат (x1, y1, z1) – и величина точечного заряда (q) в

кулонах *10-9. (За величину точечного заряда принимается действительная часть приведенного в таблице значения) . Столбцы x2 и y2 в

этой лабораторной работе не используются.

В таблице 1.3 заданы начало и конец отрезка прямой, на котором лежат точки, в которых рассчитывается электрическое поле. Расчет

15

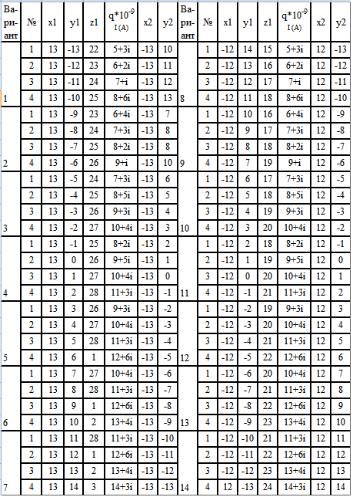
проводится в 11 точках. Эти точки должны равномерно распределяться по прямой.

Варианты задания, заряды, токи .

16

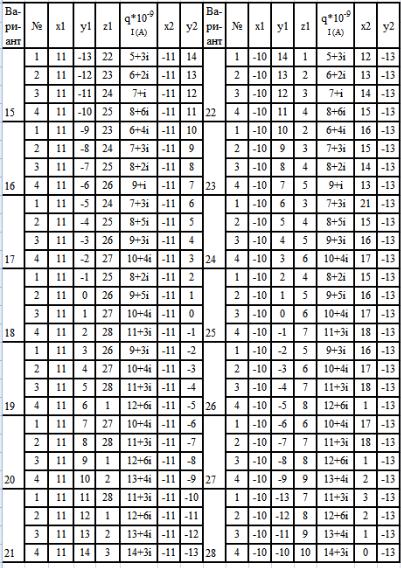
Продолжение таблицы 1.2 .

17

Выполняя лабораторную работу, следует сначала в программе MathCAD составить файл, с помощью которого можно рассчитать поле в произвольной точке, если число зарядов будет достигать 10. Отладить файл на тестовом примере (вариант 28), а затем, убедившись, что расчет проводится без ошибок, ввести исходные данные по варианту и получить результат.

Обозначение переменных:

xp, yp, zp – координаты точки, в которой рассчитывается поле;

r – двумерный массив расстояний между точками, в которые помещен заряд и точками, в которых рассчитывается поле;

fix, fiy,fiz – углы, которые составляет радиус вектор r c осями координат x, y, z;

i – номер точки, в которую помещается заряд;

xn, yn, zn, q – координаты и величина i –го заряда;

dx, dy, dz – проекция расстояния между точкой, в которой находится заряд и точкой, для которой рассчитывается электрическое поле на оси x, y, z соответственно,

E, EX, EY,EZ – электрическое поле от одного заряда и его проекции на координатные оси,

EP, EPX, EPY, EPZ – модуль суммарного вектора электрического поля от всех зарядов и его проекций на координатные оси.

sp – расстояние между точками, в которых рассчитывается электрическое поле. Это расстояние рассчитывается в плоскости хoy

10 9

– относительная диэлектрическая проницаемость;

а = * 0 – абсолютная диэлектрическая проницаемость.

Для расчета воспользуемся выражением (1.2) которое позволяет найти поле точечного заряда. В каждой точке рассчитаем поле от каждого заряда и сложим их.

Алгоритм расчета поля.

1.Введите исходные данные:

a. диэлектрическую проницаемость

19

d.координаты и величины зарядов. Переменные xn, yn, zn, q вводятся, как одностолбцовые матрицы. Столбец содержит 10 элементов. Первые 4 элемента всех столбцов вводятся в соответствии с вариантом. Остальным элементам присваивается значение 0. Можно после отладки программы некоторые или все нули заменить значениями координат и величинами зарядов, если вы решили рассчитать электрическое поле для большего их числа.

e.координаты начальной и конечной точки прямой, на которой находятся точки для расчета электрического поля x1, y1, z1, x2, y2, z2.

2.Введите формулы для расчета

a.Координат точек, в которых рассчитывается электрическое поле и диэлектрической проницаемости:

b.

c. проекции на координатные оси расстояния между точками, в которых находятся заряды и точка, для которой рассчитывается электрическое поле, само расстояние и углы с координатными осями. Будет рассчитываться двумерные массивы значений, поэтому формулы должны выглядеть так:

Индексы k, i означают, что рассчитывается величина (например, расстояние rk,i) в k – ой точке от i-ой точки;

20