В.С.Матющенко - ТОЭ
.pdf
Два комплексных числа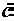 
и 
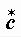называются сопряженными, если они имеют одинаковые модули и равные по величине, но разные по знаку аргументы
(рис. 2.10):
,
=
.
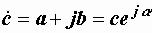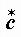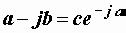Изображающие их векторы симметричны относительно вещественной оси.
Действия над комплексными числами.
Сложение и вычитание производится над числами, записанными в алгебраической форме: Рис. 2.10. Сопряженные комплексные
числа
=
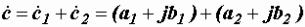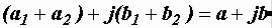, т.е.
складываются по отдельности вещественные и мнимые части слагаемых: а =
а1+а2, b = b1+b2. Операции сложения комплексных чисел соответствует сложение изображающих их векторов.
Сумма сопряженных комплексных чисел равна удвоенному значению вещественной части:
+
=
.
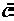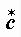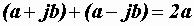Умножение и деление комплексных чисел удобнее всего производить в показательной форме. Модули при этом перемножаются или делятся, а аргументы складываются или вычитаются:
(2.7)
где с = с1 с2, α =α 1+α 2;
,
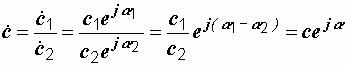где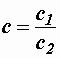 
, α =α 1 – α 2 .
Что происходит с векторами при перемножении комплексных чисел?
Изобразим на комплексной плоскости два вектора: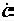 
1 – первый сомножитель и 
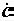– результирующий (рис. 2.11). Последний получается умножением 
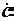1 на комплексное число с2е jα 2.
На рис. 2.11 мы видим, что при умножении длина вектора возросла в с2 раз, а аргумент увеличился на α 2.
Рассматривая комплексное число как вектор, мы приходим к следующему выводу.
При умножении вектора на комплексное число ае jα , вектор растягивается в араз и поворачивается на угол α .
Рис. 2.11. Перемножение
комплексных чисел
Так как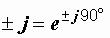 
, то при умножении вектора на ± j он поворачивается на угол ± 90° (рис. 2.12).
Произведение сопряженных комплексных чисел равно квадрату модуля комплексного числа:
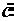x 
,
или
Иногда приходится производить умножение и деление комплексных чисел в алгебраической форме. Перемножение выполняется по правилам
умножения многочленов с учетом того, что j2 = -1
Рис. 2.12. Умножение вектора на ± j
=
.
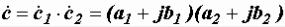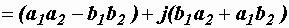При делении, чтобы получить результат, необходимо избавиться от мнимой единицы в знаменателе. Этого можно достичь умножением числителя и знаменателя на сопряженный знаменатель:
где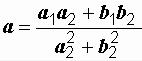 
; 
.
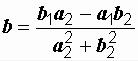2.6. Представление синусоидальных функций времени комплексными числами
Пусть задано выражение синусоидального тока i = Imsin(ω t+ψ ). Как мы видели раньше, этому выражению соответствует вектор, длина которого
равна Im, а угол наклона к горизонтальной оси ψ . Если этот вектор изобразить в комплексной плоскости (рис. 2.13), то его можно обозначить
комплексным числом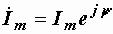 
, которое называется комплексной амплитудой тока.
Рис. 2.13. Вектор тока на комплексной плоскости
Комплексное действующее значение тока получается делением последнего выражения на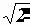 
:
.
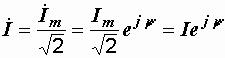Здесь и дальше буквами с точкой над ними (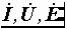
) обозначаются комплексные числа, представляющие синусоидальные функции времени. Это ток, напряжение и ЭДС. Комплексные сопротивление и проводимость
обозначаются прописными буквами Z и Y , а их модули строчными z и y. Комплексная мощность обозначается буквой S с волнистым значком
(тильда) над ней: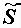 
.
2.7. Способы задания синусоидального тока
Как следует из вышесказанного, синусоидальный ток можно задать
четырьмя различными формами: уравнением i = Imsin(ω t + ψ ), определяющим мгновенное значение тока (значение тока в любой момент времени), волновой диаграммой, вектором и комплексным числом. При этом мы легко можем перейти от одной формы задания к другой.
Например:
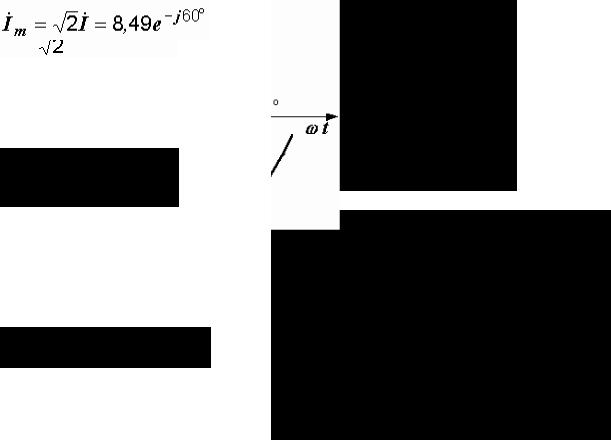
1) i = 20sin(ω t+110° ),
,
;
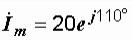2) 
,
,
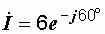i = 8,49sin(ω t-60° );
3) 
,
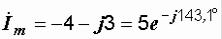i = 5sin(ω t-143,1° ),
,
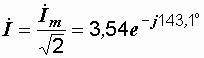u = 100 sin (ω t + 60° ).
В качестве начальной фазы мы берем не 120° , которые указаны на волновой диаграмме, а тот угол, на который сдвинуто начало синусоиды. Начальная фаза на волновой диаграмме определяется ближайшей к началу координат точкой перехода синусоиды через ноль от минуса к плюсу – это
60° . Так как начало синусоиды смещено от точки 0 влево, то начальная фаза положительна.
2.8. Законы Кирхгофа в цепях синусоидального тока. Методы расчета цепей синусоидального тока
Для мгновенных значений ЭДС, токов и напряжений остаются справедливыми сформулированные ранее законы Кирхгофа.
П е р в ы й: в любой момент времени алгебраическая сумма токов в узле электрической цепи равна нулю:
|
, |
(2.8) |
|
где n – число ветвей, сходящихся в узле.
В т о р о й: в любой момент времени в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на всех остальных элементах контура:
|
, |
(2.9) |
|
где m – число ветвей, образующих контур.
Токи, напряжения и ЭДС, входящие в уравнения (2.8) и (2.9), есть синусоидальные функции времени, которые мы рассматриваем как проекции некоторых векторов на оси координат. Так как сложению проекций соответствует сложение векторов и соответствующих им комплексных чисел, то справедливыми будут следующие уравнения, которые можно записывать как для действующих, так и для амплитудных значений.
Законы Кирхгофа |
Законы Кирхгофа |
||||
в векторной форме: |
в символической форме: |
||||
|
|
|
(2.11) |
||
|
|
(2.10) |
|
|
|
|
|
||||
Из сказанного вытекают три возможных подхода к расчету цепей синусоидального тока: выполнение операций непосредственно над синусоидальными функциями времени по уравнениям (2.8) и (2.9); применение метода векторных диаграмм, основанного на уравнениях (2.10), использование в расчетах комплексных чисел и уравнений (2.11), являющихся основой символического метода.
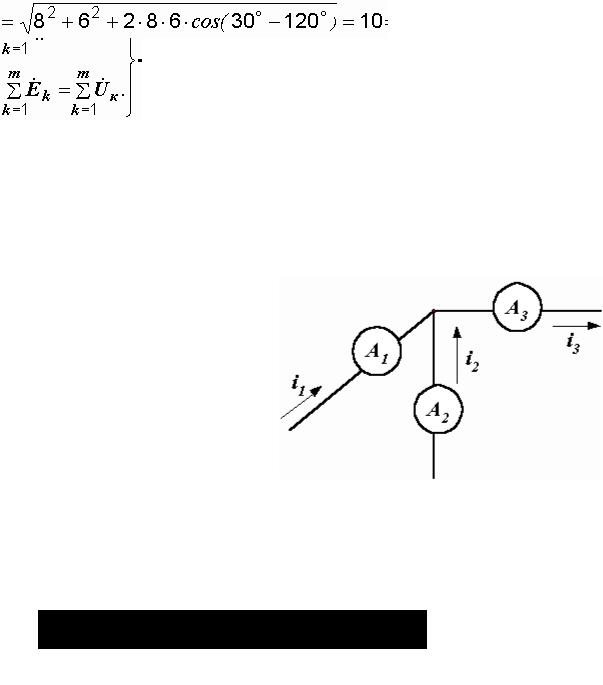
Пример 2.4. В узле электрической цепи сходятся три ветви (рис. 2.14).
Токи первых двух ветвей известны:
i1 = 8sin(ω t+30° ) А, i2 = 6sin(ω t+120° ) А.
Требуется записать выражение тока i3 и определить показания амперметров электромагнитной системы.
Рис. 2.14. Узел электрической цепи
Р е ш е н и е. 1. Непосредственное сложение синусоид:
i3 = i1+i2 = 8sin(ω t+30° )+6sin(ω t+120° ) = I3msin(ω t+ψ 3).
Сумма двух синусоид одинаковой частоты есть тоже синусоида той же частоты. Ее амплитуда и начальная фаза могут быть найдены по известным из математики формулам:
A,
,
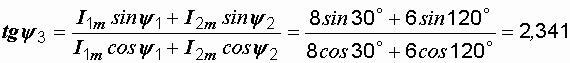откуда ψ 3 = 66,87° . Итак, i3 = 10sin (ω t+66,87° ).
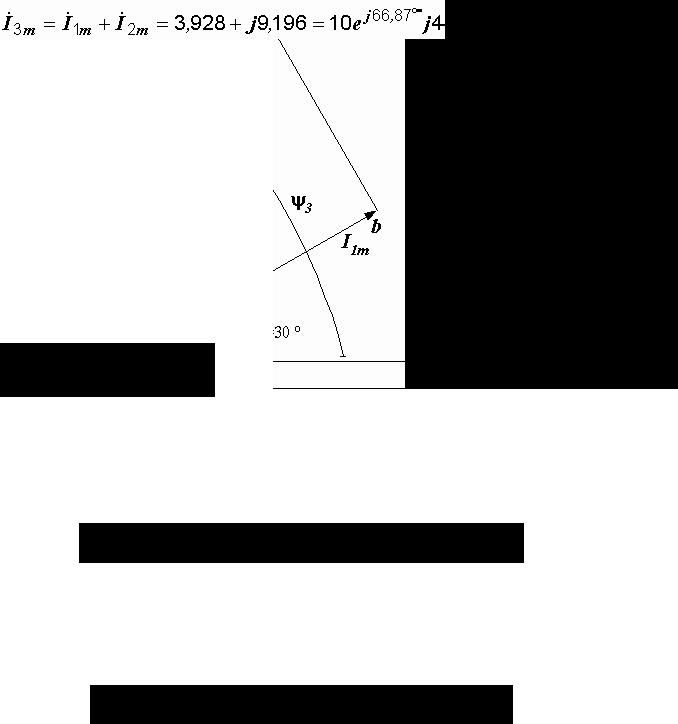
2.Применение метода векторных диаграмм.
Всоответствии с первым законом Кирхгофа в векторной форме для цепи на
рис. 2.14 имеем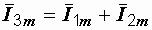 
. В прямоугольной системе координат
строим векторы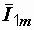 
и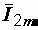 
и находим вектор 
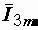, равный их сумме (рис. 2.15).
Так как треугольник oab прямоугольный, а
сторона ab равна длине вектора I2m, то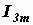 
=
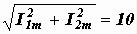А.
Если треугольник получается не прямоугольным, то применяется теорема косинусов.
Начальная фаза третьего тока равна углу наклона: вектора I3m к горизонтальной
оси: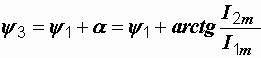
Рис. 2.15. Векторная диаграмма токов
3. Решение символическим методом.
Записываем комплексные амплитуды первого и второго токов:
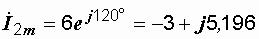A,
A.
По первому закону Кирхгофа в символической форме
А.
Модуль последнего комплексного числа равен амплитуде третьего тока, а аргумент – начальной фазе.
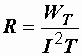
Определяем показания амперметров. Приборы электромагнитной системы показывают действующие значения токов и напряжений, поэтому
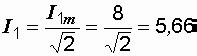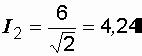A,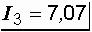 
A, 
A.
Обращаем внимание на то, что 
. Это не ошибка. В цепях синусоидального тока для показаний приборов законы Кирхгофа не справедливы. Можно складывать мгновенные значения токов (синусоидальные функции времени), векторы и комплексные числа, но не численные значения токов и напряжений, не показания приборов.
Следует заметить, что первый из рассмотренных в примере методов из-за громоздкости вычислительных операций с синусоидами практически не применяется.
Метод векторных диаграмм удобен при решении относительно несложных задач.
В символической форме, как будет показано ниже, можно рассчитать сколь угодно сложную линейную цепь.
2.9. Понятие об активном сопротивлении. Синусоидальный ток в активном сопротивлении
При протекании электрического тока выделяется энергия в виде тепла или механической работы. Параметр электрической цепи, характеризующий этот процесс, называется активным сопротивлением. Количественно он определяется следующим образом. Пусть на некотором участке цепи за
время Т, равное периоду переменного тока, действующее значение которого I, необратимо преобразуется в тепло или механическую работу
электрическая энергия WТ. Тогда активное сопротивление рассматриваемого участка цепи по определению равно
|
. |
(2.12) |
|
На схеме активное сопротивление обозначается точно так же, как и сопротивление постоянному току (рис. 2.16). Последнее, называемое еще омическим, определяется структурой кристаллической решетки проводника и состоянием свободных электронов. Наличие вблизи каких-либо проводящих тел и ферромагнитных сердечников на омическое сопротивление не влияет.
Иначе обстоит дело при переменном токе.
Рис. 2.16. Активное сопротивление
При невысоких частотах сопротивление проводника мало отличается от сопротивления постоянному току. Но с повышением частоты все сильнее и сильнее сказывается поверхностный эффект, заключающийся в вытеснении переменного тока из серединных областей проводника к его поверхности.
Это приводит к уменьшению сечения, занимаемого током, к увеличению сопротивления и возрастанию тепловых потерь. К аналогичным последствиям приводит и эффект близости, выражающийся в возникновении неравномерности распределения электрического тока по сечению проводника из-за действия магнитного поля соседних проводов.
Если вблизи катушки имеются ферромагнитные сердечники и какие-либо другие проводящие тела, то магнитное поле переменного тока индуцирует в них вихревые токи, что вызывает дополнительные потери энергии на нагрев. Кроме того, в переменном магнитном поле происходит непрерывное периодическое перемагничивание ферромагнитного сердечника, требующее энергетических затрат на изменение направления магнитных моментов доменов.
Таким образом, понятие активного сопротивления является более широким, по сравнению с омическим. Числитель в формуле (2.12) при переменном токе всегда больше, чем при постоянном, так как он включает в себя все перечисленные потери электромагнитной энергии на тепло. Поэтому для одной и той же электрической установки активное сопротивление переменному току всегда оказывается больше чем сопротивление постоянному току.
Мгновенные значения напряжения и тока в активном сопротивлении связаны законом Ома:
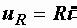или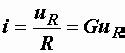 
,
где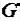 
– активная проводимость: 
.
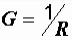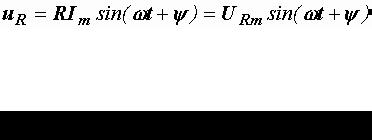
При изменении тока по синусоидальному закону
|
, |
(2.13) |
|
напряжение тоже синусоидально и имеет с током одинаковые начальные фазы:
. (2.14)
Отсюда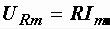 
или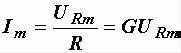 
.
Разделив два последних уравнения на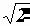 
, получим
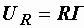и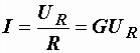 
.
Четыре последних уравнения представляют собой различные формы записи закона Ома для активного сопротивления.
По уравнениям (2.13) и (2.14) можно записать комплексные амплитуды тока и напряжения:
, 
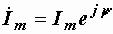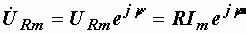, откуда
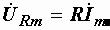или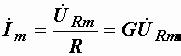 
.
После деления последних двух уравнений на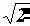 
будем иметь:
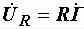и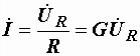 
.
Получили те же самые выражения закона Ома, но в символической форме.
На рис. 2.17 показаны волновая и векторная диаграммы, построенные по формулам (2.13) и (2.14).