
В.С.Матющенко - ТОЭ
.pdf
Произвольно задавшись направлениями токов в ветвях и принимая токи, подтекающие к узлу, положительными, а оттекающие от узла – отрицательными, записываем:
узел а:
узел в: |
(1.6) |
узел с:
Число независимых уравнений в первом законе Кирхгофа – на единицу меньше числа узлов, поэтому для последнего узла d уравнение не пишем.
В заданной схеме семь ветвей, семь неизвестных токов. Система (1.6) содержит только три уравнения. Недостающие четыре записываем по второму закону Кирхгофа.
Второй закон Кирхгофа: в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех сопротивлениях контура.
Число уравнений, составляемых по этому закону, равно числу взаимно независимых контуров. При рассмотрении схемы каждый последующий контур является независимым относительно предыдущих, если он отличается от них хотя бы одной новой ветвью. В заданной схеме таких контуров четыре. Они отмечены пронумерованными дугообразными стрелками. Любой другой контур новых ветвей не содержит, поэтому не является независимым. Дугообразные стрелки показывают произвольно выбранные направления обхода контуров. Если направления ЭДС и токов совпадают с направлением обхода контура, то они записываются с плюсом, если не совпадают – то с минусом.
контур 1:
контур 2:
(1.7)
контур 3:
контур 4:
Системы (1.6) и (1.7) дают достаточное количество уравнений для отыскания всех неизвестных токов.
1.3.2. Метод узловых потенциалов
Уравнения, составляемые по этому методу, называются узловыми уравнениями. В качестве неизвестных они содержат потенциалы узлов,

причем один из них задается заранее – обычно принимается равным нулю.
Пусть таким узлом будет узел d: ϕ d = 0. Равенство нулю какой-то точки схемы обычно показывается как ее заземление.
Запишем для каждой ветви выражение закона Ома:
(1.8)
Подставляя формулы (1.8) в систему (1.6) после несложных преобразований получаем следующие уравнения, количество которых на единицу меньше числа узлов:
(1.9)
При решении практических задач указанный вывод не делают, а узловые уравнения записывают сразу, пользуясь следующим правилом.
Потенциал узла, для которого составляется уравнение (например, в первом уравнении последней системы – это узел а), умножается на сумму
проводимостей ветвей, присоединенных к этому узлу: ϕ а (G1+G2+G3).Это произведение записывается в левой части уравнения со знаком плюс.
Потенциал каждого соседнего узла (b и с) умножается на проводимости ветвей, лежащих между этим (соседним) узлом и узлом, для которого составляется уравнение.
Эти произведения ϕ b (G1 + G2) и ϕ сG3 записываются со знаком минус.
В правой части уравнения стоит алгебраическая сумма произведений ЭДС на проводимости тех ветвей, которые присоединены к рассматриваемому узлу:
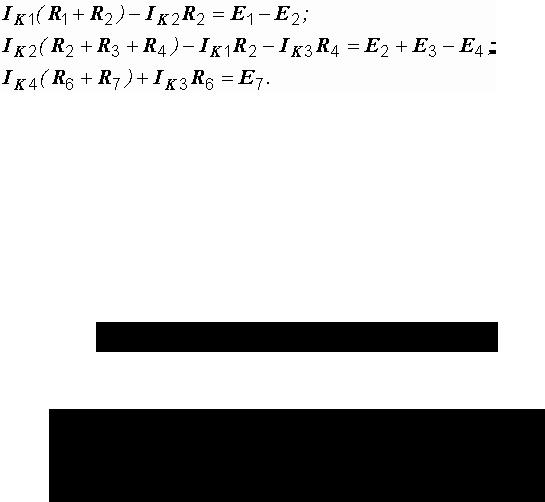
E1G1, E2G2 и E3G3. Эти произведения записываются с плюсом, если ЭДС направлены к узлу, и с минусом, если от узла.
Найдя из (1.9) потенциалы узлов и подставляя их в (1.8), определяем токи ветвей.
1.3.3. Метод контурных токов
Для каждого из взаимно независимых контуров назначается так называемый контурный ток, замыкающийся по всем ветвям контура. Направления этих токов произвольны.
На рис. 1.9 они обозначены дугообразными стрелками, рядом с которыми
стоят буквы IK1, IK2, IK3 и IK4. Для выбранных контурных токов записываются уравнения по второму закону Кирхгофа. Контур при этом обходится по направлению контурного тока. Рассмотрим порядок
составления уравнения на примере третьего контура. Контурный ток IK3, протекая по сопротивлениям своего контура, создает на них падение напряжения
(1.10)
По сопротивлению R4, являющемуся элементом третьего контура, протекает контурный ток IK2. Создаваемое им падение напряжения IK2R4 вычитается из предыдущего, так как направление тока IK2 в сопротивлении R4 противоположно току IK3. Сопротивление R6 также входит в третий контур. Падение напряжения на нем, создаваемое контурным током IK4,
складывается с суммой (1.10), так как направления IK4 и IK3 в R6 одинаковы. В правой части уравнения записывается алгебраическая сумма всех ЭДС
контура, в данном случае – единственная ЭДС E4.
Итак, для третьего контура имеем:
Аналогично составляются и остальные контурные уравнения:

После решения последней системы действительные токи ветвей определяются по найденным контурным:
(1.11)
Контурные уравнения получаются подстановкой формул (1.11) в уравнения второго закона Кирхгофа (1.7).
1.3.4.Метод наложения
Воснове метода лежит принцип суперпозиции (наложения): ток в любой ветви сложной электрической цепи, содержащей несколько ЭДС, может быть найден как алгебраическая сумма токов в этой ветви от действия каждой ЭДС в отдельности.
Это весьма важное положение, справедливое только для линейных цепей, вытекает из уравнений Кирхгофа и утверждает независимость действия источников энергии. Основанный на нем метод сводит расчет цепи, содержащей несколько ЭДС, к последовательному расчету схем, каждая из которых содержит только один источник.
Например, токи в схеме на рис. 1.10, а находятся как алгебраические суммы частичных токов, определяемых из схем 1.10, б и в.
Аналогично:
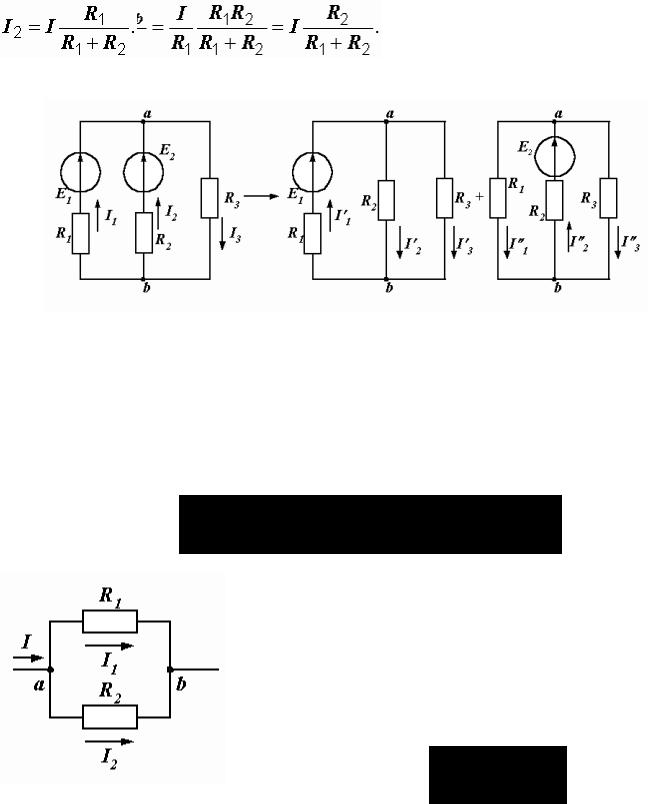
И, наконец,
|
|
|
|
|
a) |
|
б) |
|
в) |
Рис. 1.10. Заданная (а) и расчетные (б и в) схемы
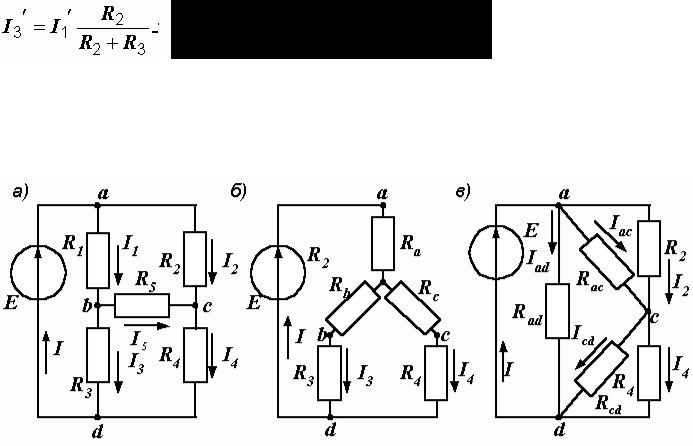
При расчете подобных схем очень удобным оказывается следующий прием. Пусть требуется определить токи в параллельных ветвях при известном суммарном токе (рис. 1.11).
Имеем:
Из полученной формулы вытекает правило: ток в одной из двух параллельных ветвей равен произведению общего тока на сопротивление соседней ветви, деленному на сумму сопротивлений параллельных ветвей.
Пользуясь этим правилом для тока I2 можно написать:
Рис. 1.11. Токи в параллельных ветвях
Применение этого правила избавляет от необходимости определять напряжения 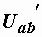 и
и 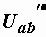 в схемах на рис. 1.10, б и 1.10, в. Так, после определения тока
в схемах на рис. 1.10, б и 1.10, в. Так, после определения тока 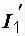 , токи
, токи 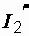 и
и  можно найти по формулам:
можно найти по формулам:
1.3.5. Эквивалентное преобразование треугольника и звезды сопротивлений
Пусть требуется рассчитать цепь, показанную на рис. 1.12, а.
Рис. 1.12. Преобразования электрической цепи
Расчет можно осуществить одним из описанных выше методов. Но так как в цепи имеется только один источник питания, наиболее простым было бы использование закона Ома. Однако попытка определения общего сопротивления цепи оказывается безрезультатной, так как здесь мы не находим ни последовательно, ни параллельно соединенных сопротивлений. Решить задачу помогает преобразование треугольника сопротивлений в эквивалентную звезду.
Треугольник и звезда сопротивлений имеют вид, показанный на рис. 1.13.
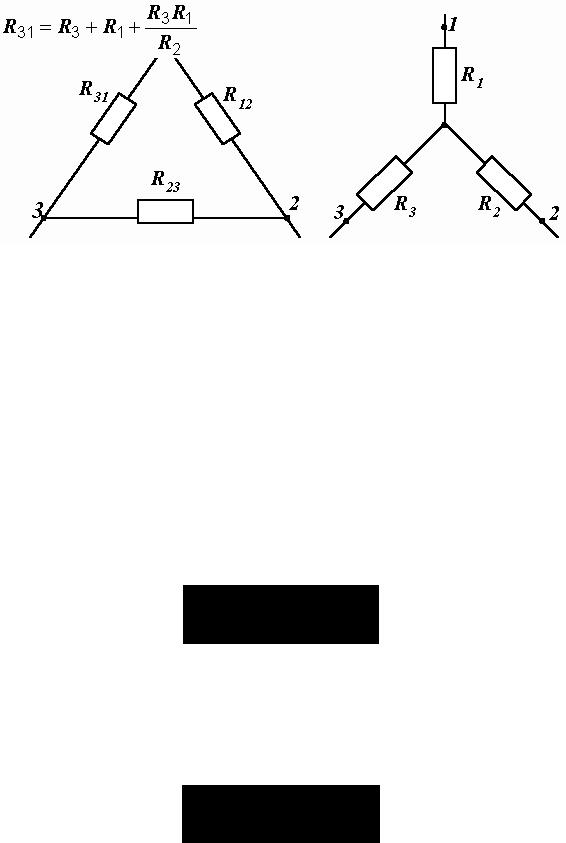
Рис. 1.13. Треугольник и звезда сопротивлений
Если при замене одной из этих схем другой не изменяются потенциалы одноименных точек и подтекающие к ним токи, то во внешней цепи также не произойдет никаких изменений. В этом случае говорят, что схемы эквивалентны.
Можно показать, что условием эквивалентности являются следующие уравнения:
а) при преобразовании треугольника в звезду:
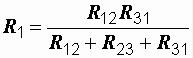 ; ;
; ;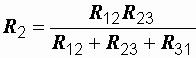
;
б) при преобразовании звезды в треугольник:
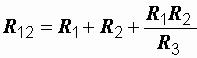 ;
; 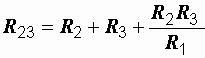 ;
;
.
Структура приведенных формул проста и легко запоминается.
Например, сопротивление звезды R1, присоединенное к узлу 1, получается перемножением сопротивлений R12 и R31 треугольника, присоединенных к
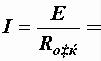
этому же узлу, и делением полученного произведения на сумму всех сопротивлений треугольника.
При обратном преобразовании сопротивление треугольника R12, лежащее
между узлами 1 и 2, равно сумме сопротивлений звезды R1 и R2, присоединенных к этим узлам, плюс их произведение, деленное на
сопротивление третьего луча звезды R3.
Пример 1.3. Рассчитать токи в цепи, изображенной на рис. 1.12, а, при следующих числовых значениях ее параметров: Е = 660 В,
R1 = 20 Ом, R2 = 30 Ом, R3 = 5 Ом, R4 = 20 Ом, R5 = 50 Ом.
а) Р е ш е н и е п р е о б р а з о в а н и е м т р е у г о л ь н и к а в з в е з д
у.
После преобразования треугольника, образованного сопротивлениями R1, R2 и R5, в звезду, получаем схему, показанную на рис. 1.12, б. Обращаем
внимание на то, что токи в непреобразованной части схемы (I, I3 и I4) остались теми же.
Сопротивления звезды определяем по сформулированному выше правилу:
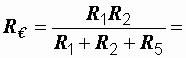 6 Ом;
6 Ом; 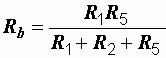 = 10 Ом;
= 10 Ом;
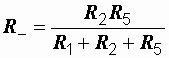 = 15 Ом.
= 15 Ом.
Теперь общее сопротивление цепи легко находится:
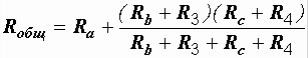 =16,5 Ом.
=16,5 Ом.
Ток, протекающий по источнику (одинаковый в заданной и преобразованной схемах), равен
40 А.
Токи в параллельных ветвях:
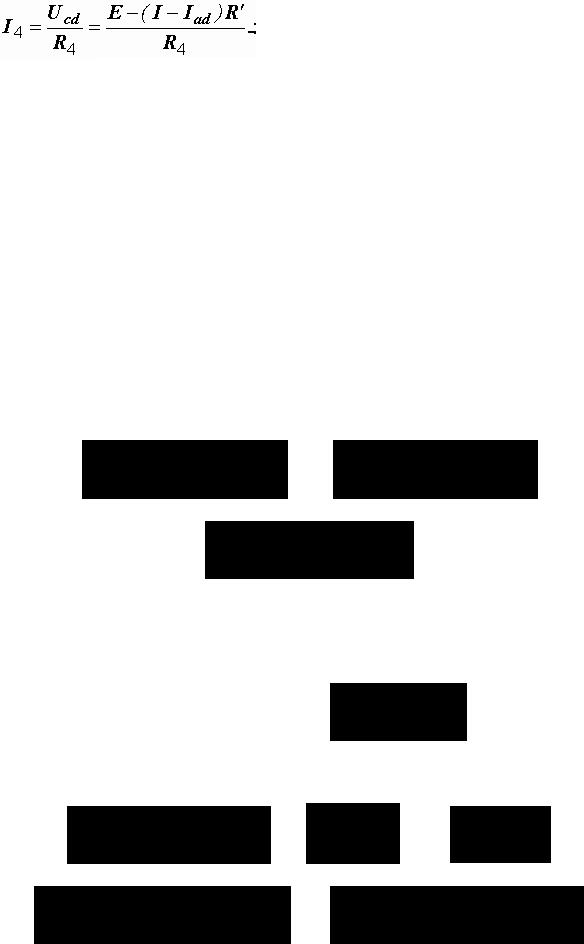
|
28 A; |
|
12 A. |
|
|
Возвращаемся к исходной схеме (рис. 1.12, а):
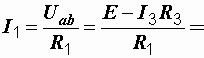 26 A;
26 A; 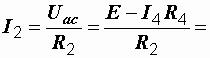 14 A.
14 A.
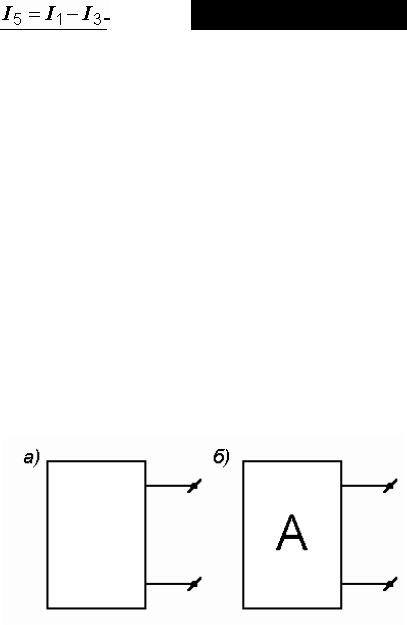
Ток в пятой ветви находим из первого закона Кирхгофа: I5 = I1–I3 = 26–28 =
–2 A. Знак минус говорит о том, что действительное направление тока I5 противоположно указанному на схеме.
б) Р е ш е н и е п р е о б р а з о в а н и е м з в е з д ы в т р е у г о л ь н и к.
Преобразуем звезду, образуемую в схеме на рис. 1.12, а сопротивлениями R1, R5 и R3, в эквивалентный треугольник (рис. 1.12, в).
Определяем сопротивления треугольника:
Теперь рассчитываем преобразованную цепь.
Сначала находим эквивалентные сопротивления участков ac и cd:
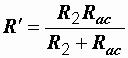 ;
;
Затем определяем общее сопротивление и токи:
Возвращаемся к исходной схеме:
Рекомендуем подставить в приведенные формулы числовые значения параметров цепи и сравнить результаты вычислений с полученными в примере 1.3а.
1.4. Пассивный и активный двухполюсники. Теорема об активном двухполюснике
Двухполюсником называется часть электрической цепи любой сложности и произвольной конфигурации, выделенная относительно двух зажимов (двух полюсов).
Двухполюсник, не содержащий источников энергии или содержащий скомпенсированные источники (суммарное действие которых равно нулю), называется пассивным. Если в схеме двухполюсника имеются нескомпенсированные источники, он называется активным. На схеме двухполюсник обозначают прямоугольником с двумя выводами (рис. 1.14). Это обозначение можно условно рассматривать как коробку, внутри которой находится электрическая цепь.
Рис. 1.14. Пассивный (а) и активный (б) двухполюсники
Пассивный двухполюсник является потребителем энергии и может быть заменен эквивалентным сопротивлением, величина которого равна входному сопротивлению двухполюсника (см., например, рис. 1.15).
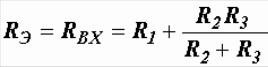 .
.
