
В.С.Матющенко - ТОЭ
.pdf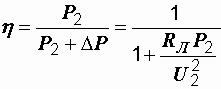
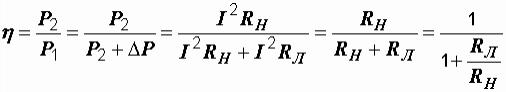 , (1.16)
, (1.16)
Из данной формулы следует, что коэффициент полезного действия передачи определяется отношением сопротивлений линии и нагрузки.
При их равенстве, когда нагрузке передается максимальная мощность, η = 0,5 = 50 %. Этот режим, при котором теряется половина передаваемой энергии, на практике, естественно, не пригоден. В реальных линиях при передаче больших мощностей КПД составляет примерно 0,94–0,97. При этом сопротивление нагрузки значительно больше сопротивления линии.
Для анализа режимов электропередачи полезной оказывается еще одна
формула. Так как 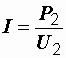 , а
, а  , то
, то
|
. |
(1.17) |
|
То есть при одной и той же мощности нагрузки Р2, потери ∆ Р пропорциональны сопротивлению линии и обратно пропорциональны квадрату напряжения. Для увеличения коэффициента полезного действия передачи необходимо повышение напряжения и снижение электрического сопротивления проводов линии путем увеличения их сечения и применения материалов с меньшим удельным сопротивлением.
Пример 1.6. Линия электропередачи с проводами марки А-120 длиной l =
1000 км питает нагрузку мощностью Р2 = 50 МВт. Каким должно быть напряжение в начале линии, чтобы КПД передачи был не ниже 90 %?
Р е ш е н и е. Сопротивление одного километра провода марки А-120 R0 = 0,27 Ом/км. Суммарное сопротивление прямого и обратного проводов линии
составляет RЛ = 2lR0 = 540 Ом.
Принимая η = 0,9, из формулы (1.17) получаем:
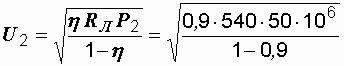 = 4,93 x 105 В = 493 кВ.
= 4,93 x 105 В = 493 кВ.
Так как 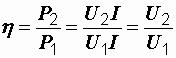 , то
, то 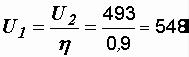 кВ.
кВ.
Для выполнения условий задачи напряжение в начале линии должно быть не ниже 548 кВ.
2.Электрические цепи однофазного синусоидального тока
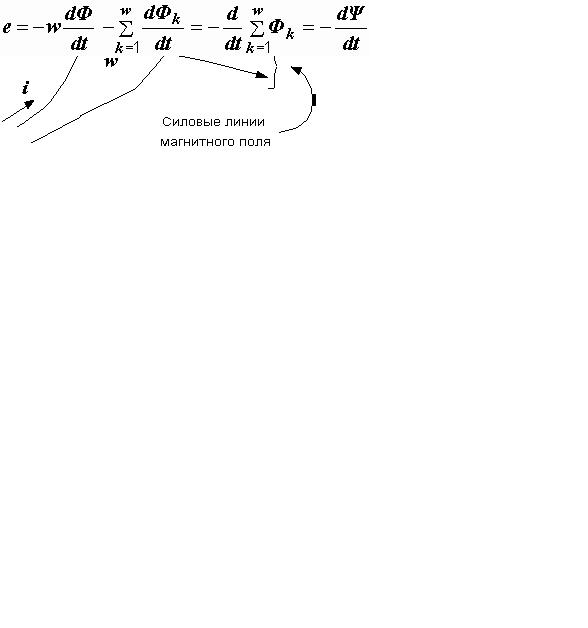
2.1.Закон электромагнитной индукции
Пусть имеется катушка, содержащая w витков (рис. 2.1) и помещенная в переменное магнитное поле.
|
|
В каждом витке такой катушки индуцируется |
||
|
|
ЭДС электромагнитной индукции. Если |
||
|
|
магнитный поток, пронизывающий k-тый виток, |
||
|
|
обозначить Фk, то ЭДС этого витка будет равна |
||
|
|
|
|
. |
|
|
|
|
|
Рис. 2.1. Катушка в магнитном поле |
|
|
||
|
||||
|
|
|
||
Так как все витки катушки соединены последовательно, то их суммарная ЭДС равна
|
, |
(2.1) |
|
где 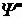 – потокосцепление катушки, определяемое как сумма магнитных
– потокосцепление катушки, определяемое как сумма магнитных
потоков всех витков: 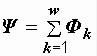 .
.
Единица измерения потокосцепления такая же, как и у магнитного потока – вольт-секунда (Вс); Ее название – вебер (сокращенно Вб).
Если все витки катушки, пронизываются одним и тем же магнитным потоком, т.е. если Ф1 = Ф2 = ... = Фk = Фw = Ф, то
|
и |
|
. |
(2.2) |
|
|
|||
|
|
2.2. Получение синусоидальной ЭДС. Характеристики синусоидальных величин. Обозначения в цепях переменного тока
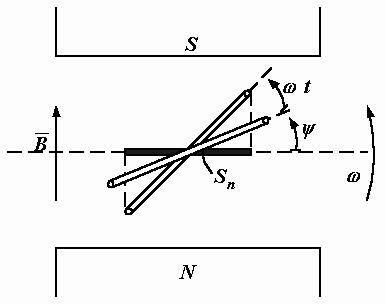
Пусть в однородном магнитном поле, например, между полюсами плоского
магнита, под углом 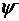 к горизонтальной плоскости расположена плоская катушка, выполненная в виде прямоугольной рамки, по периметру которой
к горизонтальной плоскости расположена плоская катушка, выполненная в виде прямоугольной рамки, по периметру которой
намотано w витков (рис. 2.2). Площадь сечения рамки – S, магнитная индукция – В.
Рис. 2.2. Получение синусоидальной ЭДС
Заставим эту катушку вращаться против часовой стрелки с угловой скоростью ω . Если обозначить время полного оборота катушки через Т, то
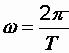 , рад/с. За некоторый промежуток времени t рамка повернется на
, рад/с. За некоторый промежуток времени t рамка повернется на
угол ω t. Площадь проекции рамки в этом положении 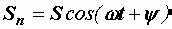 . Рамка и ее проекция на горизонтальную плоскую поверхность пронизываются одним и тем же числом силовых линий магнитной индукции, поэтому обусловленный ими магнитный поток равен
. Рамка и ее проекция на горизонтальную плоскую поверхность пронизываются одним и тем же числом силовых линий магнитной индукции, поэтому обусловленный ими магнитный поток равен
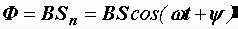 .
.
При вращении катушки число силовых линий, охватываемых ее витками, все время меняется.
Например, при горизонтальном положении рамки это число максимально, при вертикальном – равно нулю. Другими словами, меняется магнитный
поток, пронизывающий катушку, в результате чего в ней в соответствии с уравнением (2.2) наводится ЭДС:
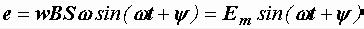 .
.
Поясним величины, входящие в последнее выражение. Еm – максимальное значение или амплитуда ЭДС. Аргумент синусоидальной
функции ω t +ψ называется фазой. Угол ψ , определяющий начальное
положение рамки и равный фазе в начальный момент времени (при t = 0), – начальная фаза. Фаза с течением времени (при вращении катушки) постоянно меняется. Скорость изменения фазы ω называется угловой или циклической частотой. Время одного цикла изменения фазы (время одного
оборота рамки) называется периодом и обозначается T. Количество полных
изменений синусоидальной ЭДС в секунду определяет частоту ƒ , измеряемую в герцах (Гц). Один герц соответствует одному полному колебанию в секунду. Связь между частотой и периодом выражается
формулой ƒ = 1/Τ . При частоте 50 Гц 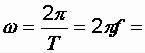 314 c-1.
314 c-1.
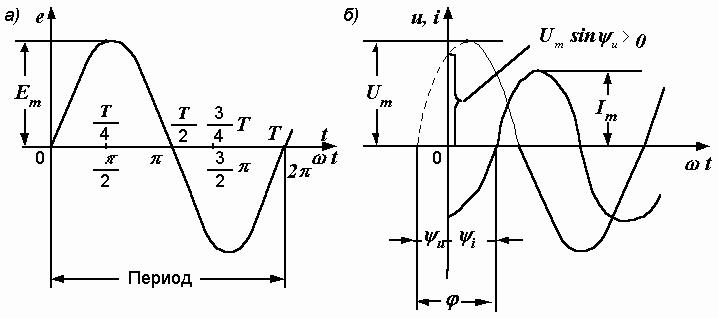
Графическое изображение синусоидальной функции времени в электротехнике называют волновой диаграммой. При ее построении на
горизонтальной оси откладывается время t или пропорциональный ему угол
ω t. При нулевой начальной фазе кривая выходит из начала координат и через каждые четверть периода принимает максимальные значения и
переходит через ноль. График такой функции построен по уравнению е = Еm sinω t на рис. 2.3, а.
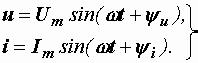
Рис. 2.3. Волновые диаграммы
При ненулевых начальных фазах диаграммы имеют несколько иной вид. Пусть напряжение и ток на некотором участке цепи определяются выражениями:
(2.3)
Для определенности положим ψ u > 0, а 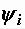 < 0. Сначала построим волновую диаграмму напряжения. При t = 0 u = Umsinψ u. При
< 0. Сначала построим волновую диаграмму напряжения. При t = 0 u = Umsinψ u. При
положительном ψ u эта величина положительна, и синусоида отсекает на вертикальной оси отрезок выше начала координат (рис. 2.3, б). Начало
синусоиды и все ее точки оказываются сдвинутыми влево на величину ψ u. Кривая тока, имея отрицательную начальную фазу, смещается вправо. Если начальные фазы двух синусоидальных функций, изменяющихся с одинаковой частотой, различны, то говорят, что они не совпадают по фазе. Отрезок на горизонтальной оси, разделяющий начала синусоидальных кривых (угол ϕ на рис. 2.3, б), определяет угол сдвига фаз. Он равен разности их начальных фаз:
ϕ = ψ u – ψ i. |
(2.4) |
В случае напряжения и тока вычисление производится именно в таком порядке: начальная фаза напряжения минус начальная фаза тока.
Если ψ u > ψ i и угол ϕ положителен, то говорят, что напряжение опережает по фазе ток, или ток отстает по фазе от напряжения. На волновой диаграмме в этом случае кривая напряжения проходит через ноль и максимальные значения раньше тока; изменения тока отстают от соответствующих изменений напряжения. Мера отставания – угол ϕ .
Остановимся еще на двух моментах. В цепях синусоидального тока мы будем встречаться как с переменными, так и с постоянными величинами. Для тех и других применяются различные обозначения. Переменные величины –
функции времени – будем обозначать маленькими (строчными) буквами u, i, e, а постоянные – большими (прописными) U, I, Е.
Второй момент касается указания направления тока или напряжения. При постоянном токе его направление связано с движением положительно заряженных частиц. В случае переменного тока его стрелка на схеме показывает у с л о в н о в ы б р а н н о е положительное направление. Если в
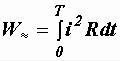
какой-то момент времени ток направлен по стрелке, он считается положительным, в противном случае он отрицателен.
2.3. Действующее значение переменного тока
Понятие действующего значения тока вводится в связи с необходимостью производства измерений. Что измерять у переменного тока? Если бы мы имели дело только с синусоидами – кривыми одной формы, то можно было бы измерять амплитуды. Но на практике встречаются самые разные кривые, и может оказаться так, что два различных по форме тока имеют одинаковые амплитуды, хотя очевидно, что на электрическую цепь они будут оказывать разное воздействие.
Поэтому наиболее целесообразно оценивать величину тока по той работе, которую он совершает. При такой оценке действие переменного тока сравнивается с аналогичным действием постоянного тока. Например, если некоторый переменный ток выделяет на участке цепи такое же количество тепла, что и постоянный ток силой 10 ампер, то говорят, что величина этого переменного тока составляет 10 ампер. Это значение тока и называют действующим.
Итак, действующим значением переменного тока называется численное значение такого постоянного тока, который за время, равное одному периоду, выделяет в сопротивлении такое же количество тепла, что и ток переменный.
Таким образом, для оценки величины переменного тока мы должны сделать следующее.
1. Определить количество теплоты, выделяющейся в сопротивлении R за время Тпри протекании переменного тока i. Это количество теплоты равно
.
` 2. Подобрать такой постоянный ток I, который за то же время Тв том же сопротивлении R выделяет такое же количество тепла. При постоянном токе
оно равно 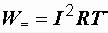 .
.
3. Приравнять W≈ и W=:
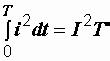 ,
,
откуда
|
. |
(2.5) |
|
Последняя формула и определяет действующее значение переменного тока.
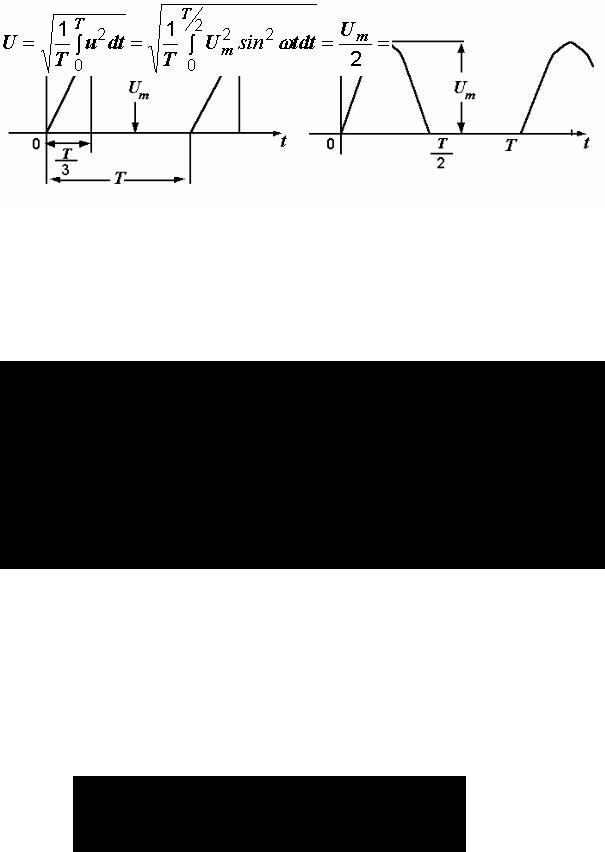
Пример 2.1. На вход некоторой цепи подается импульсное напряжение треугольной формы (рис. 2.4, а). Чему равно его действующее значение?
Р е ш е н и е.
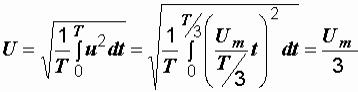 .
.
Рис. 2.4. Переменные напряжения различной формы
Пример 2.2. На рис. 2.4, б показана кривая напряжения на выходе схемы однофазного однополупериодного выпрямления. Чему равно действующее
значение напряжения, если его амплитудное значение Um составляет 311 В?
Р е ш е н и е.
155,5 В.
Пример 2.3. Определить действующее значение синусоидального тока
 .
.
Р е ш е н и е.
 .
.
Рассмотренные примеры показывают, что действующее значение переменного тока зависит от его формы.
У синусоидального тока оно равно амплитуде, деленной на 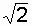 .
.
2.4. Представление синусоидальной функции времени вращающимся вектором. Векторные диаграммы
Пусть в прямоугольной системе координат имеется вектор длиной Im, расположенный под углом ψ к горизонтальной оси (рис. 2.5). Заставим этот вектор вращаться против часовой стрелки c угловой скоростью ω . Тогда за
время t он повернется на угол ω t.
Проекцию вектора на вертикальную ось обозначим i. Из треугольника oab она равна
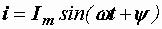 , т.е. представляет собой
, т.е. представляет собой
|
функцию, определяющую мгновенное значение |
|
тока. Таким образом, последняя может быть |
|
представлена как проекция на вертикальную |
|
ось вращающегося вектора. Изображение тока |
|
с помощью вектора называется его векторной |
|
диаграммой. Длина вектора может быть равна |
|
амплитудному Im, либо действующему |
Рис. 2.5. Вращающийся вектор |
значению I. |
Обычно вектор при этом показывается не в произвольный момент времени t,
а в начальный (t = 0), когда его угол наклона к горизонтальной оси равен начальной фазе.
Теперь по уравнениям (2.3) построим векторную диаграмму двух векторов
– тока и напряжения (рис. 2.6).
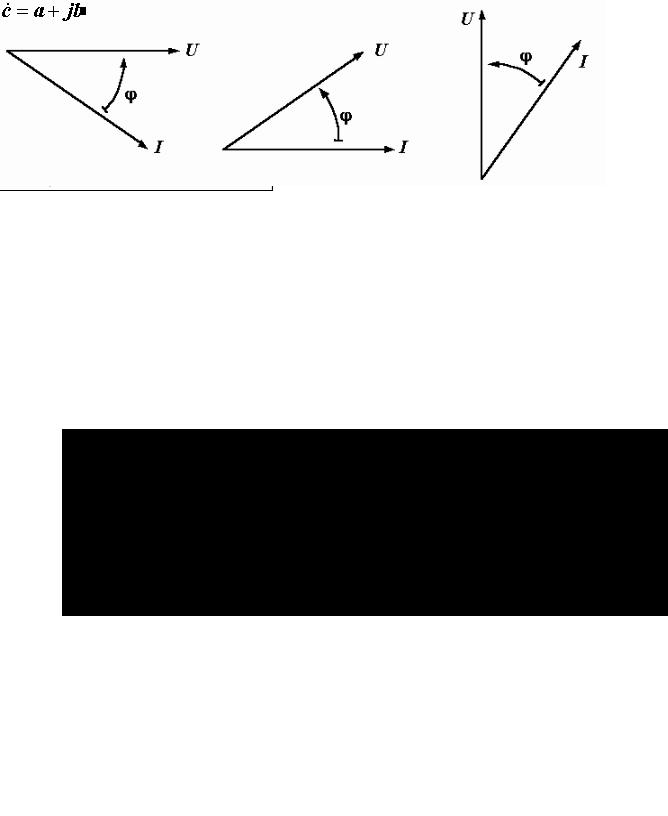
Рис. 2.6. Векторная диаграмма тока и напряжения
Длины векторов равны действующим значениям, углы их наклона к горизонтальной оси – начальным фазам, а угол
между векторами, равный разности начальных фаз ψ u и ψ i,
в соответствии с уравнением (2.4) определяет сдвиг фаз напряжения и тока.
Подчеркиваем, что на диаграмме стрелка, отмечающая угол ϕ , всегда направляется от вектора тока к вектору напряжения. Сейчас она направлена в положительном направлении – против часовой стрелки.
Векторная диаграмма дает наглядное представление об отставании одних величин и опережении других. Если вращать картинку, показанную на рис. 2.6, против часовой стрелки, то вектор тока будет отставать от напряжения на угол ϕ . Так как при вращении длины векторов и угол между ними не меняются, то в том случае, когда начальные фазы напряжения и тока нас не интересуют, мы можем изображать диаграмму без осей и располагать ее так, как нам удобно (рис. 2.7).
Рис. 2.7. Варианты построения векторной диаграммы
2.5. Основные сведения о комплексных числах
Комплексным числом называется выражение вида
|
, |
(2.6) |
|
где  – обозначение комплексного числа; a и b – соответственно
– обозначение комплексного числа; a и b – соответственно
действительная и мнимая части комплексного числа; 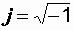 – мнимая единица.
– мнимая единица.
Величины a и b часто обозначают следующим образом: a = Re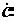 , b =
, b =
Im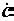 . Символы Re и Im – есть начальные буквы английских слов Real – действительный и Imaginary – мнимый.
. Символы Re и Im – есть начальные буквы английских слов Real – действительный и Imaginary – мнимый.
Геометрически комплексное число изображается вектором на комплексной плоскости (рис. 2.8). Горизонтальная и вертикальная оси, отмеченные соответственно знаками + и
+j, называются действительной (или вещественной) и мнимой. Действительная и мнимая составляющие комплексного числа представляют собой проекции вектора на эти оси.
Рис. 2.8. Вектор на комплексной плоскости
= χ 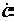 χ – модуль комплексного числа, равный длине вектора, а α = arg
χ – модуль комплексного числа, равный длине вектора, а α = arg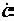 – аргумент комплексного числа. Так как а = c cosα , а
– аргумент комплексного числа. Так как а = c cosα , а
b = csinα , то 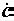 = c (cosα + j sinα ) – тригонометрическая форма
= c (cosα + j sinα ) – тригонометрическая форма
комплексного числа. С помощью формулы Эйлера 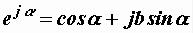
последняя преобразуется в показательную форму 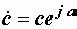 . Применяется
. Применяется
еще и полярная форма 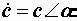 , в самой простой форме задающая модуль и аргумент комплексного числа.
, в самой простой форме задающая модуль и аргумент комплексного числа.
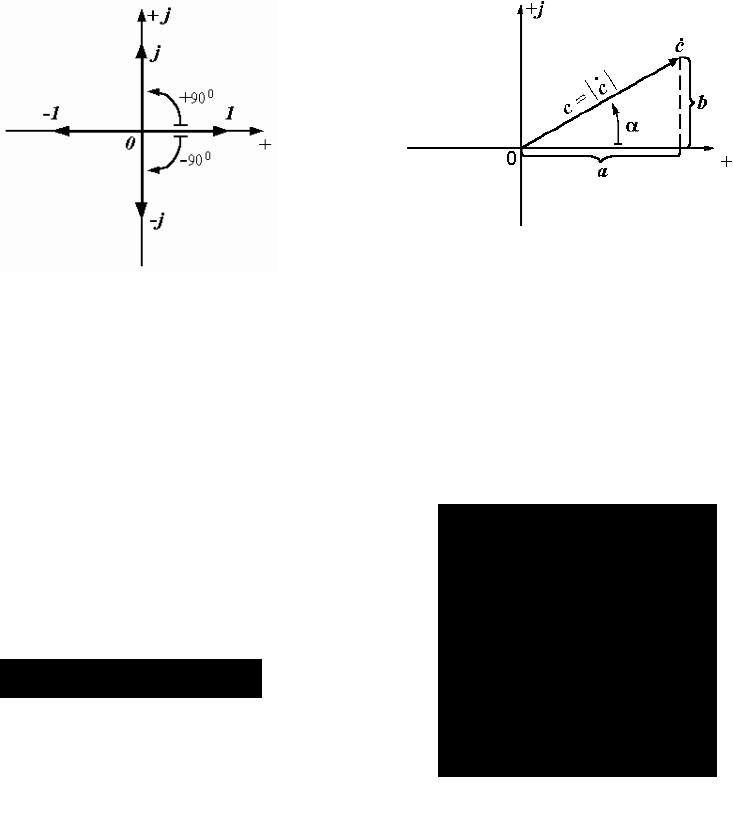
Свойства мнимой единицы (рис. 2.9):
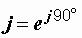 ,
, 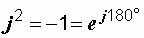 ,
,
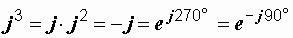 ,
,
,
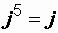 и т.д.,
и т.д.,
|
|
Рис. 2.9. Единичный вектор |
|
. |
в комплексной плоскости |
|
