
Бобрин Миронов РУКОВОДСТВО К РЕШ.ЗАДАЧ Ч
.1.PDFМинистерство транспорта Российской Федерации Федеральное агентство железнодорожного транспорта ГОУ ВПО «Дальневосточный государственный университет путей сообщения»
Кафедра «Строительная механика»
В.А. Бобрин Л.П. Миронов
РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ ПО СТРОИТЕЛЬНОЙ МЕХАНИКЕ
ЧАСТЬ 1
Рекомендовано Дальневосточным региональным учебно-методическим центром (ДВ РУМЦ)
в качестве учебного пособия для студентов специальностей 270102 «Промышленное и гражданское строительство», 270201 «Мосты и транспортные тоннели», 270204 «Строительство железных дорог, путь и путевое хозяйство», 190205 «Подъемно-транспортные, строительные,
дорожные машины и оборудование» вузов региона
Хабаровск Издательство ДВГУПС
2006
УДК 624.04 (075.8)
ББК Н112я73
Б 724
Рецензенты:
Кафедра «Механика деформируемого твердого тела» Хабаровского государственного технического университета (заведующий кафедрой кандидат технических наук, доцент
А.А. Вайсфельд)
Заведующий кафедрой «Механика деформируемого твердого тела» Дальневосточного государственного технического университета
доктор технических наук, профессор
К.П. Горбачев
Бобрин, В.А.
Б 724 Руководство к решению задач по строительной механике : учеб. пособие. В 3 ч. Ч. 1 / В.А. Бобрин, Л.П. Миронов; под ред. Л.П. Миронова. – Хабаровск : Изд-во ДВГУПС, 2006. – 141 с.
Учебное пособие соответствует дисциплине «Строительная механика» по ГОС ВПО направления 271100 «Строительство» специальности 270102 «Промышленное и гражданское строительство», направления 270200 «Транспортное строительство» специальностей 270204 «Строительство железных дорог, путь и путевое хозяйство» и 270201 «Мосты и транспортные тоннели», направления 190200 «Транспортные машины и транспортнотехнологические комплексы» специальности 190205 «Подъемно-транспорт- ные, строительные, дорожные машины и оборудование».
Пособие состоит из 3 частей. В части 1 рассмотрены методы кинематического анализа и построения линий влияния усилий в статически определимых балках, арках, рамах и фермах. Подробно разобраны примеры решения типовых задач, приведены 360 вариантов задач для самостоятельного решения и ответы к ним.
Предназначено студентам всех форм обучения.
УДК 624.04 (075.8)
ББК Н112я73
ãГОУ ВПО «Дальневосточный государственный университет путей сообщения» (ДВГУПС), 2006
2
ВВЕДЕНИЕ
Настоящее пособие посвящено методам построения линий влияния усилий в плоских статически определимых стержневых системах и их использованию при расчете сооружений на действие неподвижных и подвижных нагрузок. Пособие начинается с изложения кратких сведений из теоретической механики и математики, позволяющих студентам преодолеть трудности, возникающие при использовании аппарата этих дисциплин. В пособии излагаются основные положения теории, методические указания и подробные решения типовых задач по кинематическому анализу расчетных схем сооружений, статическому и кинематическому методам построения линий влияния и расчеты по ним.
Приведены более 190 задач с 360 вариантами исходных данных для самостоятельного решения. Тематика и набор задач отражают многолетний опыт кафедры по преподаванию строительной механики. Ко всем задачам приведены ответы в числовой или графической форме.
Всовременной доступной учебной литературе отсутствуют примеры
инаборы задач для использования в аудитории с целью организации самостоятельной индивидуальной работы студентов или тестирования их знаний по разделам курса строительной механики. Настоящее пособие восполняет этот пробел.
Наличие ответов стимулирует самостоятельный поиск студентом правильных решений, которые представляются им в письменном виде. Совпадение полученного решения с ответом благотворно влияет на возникновение у студента чувства уверенности в овладении учебным материалом.
Особое значение пособие имеет для студентов заочной формы обучения, основная масса которых живет и работает в отдаленных районах, где доступ к подобной учебной литературе затруднен.
Впособии принята тройная нумерация задач и ответов к ним. Первая цифра указывает раздел, вторая – её подраздел , третья – порядковый номер задачи.
Пособие написали В.А. Бобрин: разд. 1, подразд. 3.1, 3.2, 4.2–4.6, 5.2–5.6; Л.П. Миронов: разд. 2, подразд. 3.3–3.5, 4.1, 4.7, 5.1, 5.7.
Все замечания и рекомендации по улучшению данного пособия будут с благодарностью приняты авторами.
3

1.ЭЛЕМЕНТЫ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ И МАТЕМАТИКИ
1.1.Проекции плоской системы сил на оси прямоугольной системы координат. Моменты сил
В строительной механике широко используется аппарат теоретической механики и математики. Ниже напоминаются некоторые необходимые при расчетах стержневых систем элементы указанных дисциплин. Общепринято считать проекции сил, совпадающие (несовпадающие) с положительным направлением координатных осей, со знаком плюс (минус). Положительное направление вращения в строительной механике допустимо принимать как по ходу, так и против хода часовой стрелки, сообразуясь с удобством вычислений. Пусть имеется плоская система сил в составе сосредоточенных сил Fi, сплошных распределенных нагрузок интенсивностью qi, и сосредоточенных моментов (пар сил) mi (рис. 1.1).
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
Силовая плоскость |
|
= -R sinβ |
|
|
Центр |
|
|||||
|
Линия действия F1 |
|
R |
qi=q(ξ) |
|
|||||||
|
|
тяжести |
|
|||||||||
|
|
|
|
|
F3y= -F3sinα3 |
|
qy |
q |
|
|||
|
F1y= F1sinα1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
F1 |
|
90° |
F3 |
|
|
|
a |
|
|
|
|
|
|
Плечо r1 |
|
|
ξ |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α1 |
|
|
F2y= -F2 |
Плечо r3=0 |
|
Rq-равнодействующая |
|
||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Идентичные |
|
|
|
|
|
|
|
|
|
|
|
|
m1 изображения |
|
|
|
|
|
|
Плечо r2 |
|
K Плечо rq |
|
|
пар сил |
|
|
|
|
|
|
90° |
|
|
|
|
|
|
|
|
|
|
|
α2=90° |
F2 |
|
|
90° |
|
|
m2 |
|
|
|
|
|
α3 |
|
β |
|
Z |
|||||
0 |
F |
1z |
= F cosα |
F3z= F3cosα3 |
|
|
|
|
R |
=–R cosβ |
|
|
|
1 |
1 |
|
|
Моментная точка |
qz |
q |
|
||||
|
|
|
|
|
|
|
|
|
|
|||
Рис. 1.1. Проекции сил (изображены светлыми стрелками) на координатные оси. Моменты сил относительно произвольной точки
Тогда алгебраическая сумма проекций всех нагрузок на ось Z составит:
4

∑ FZ = F1сosα1 + F3сosα3 – Rqсosβ, а сумма проекций этих же нагрузок на ось Y будет равна: ∑ FY = F1sinα1 – F2 – F3sinα3 – Rqsinβ,
а
где Rq = ò q(ξ)dξ – равнодейcтвующая |
|
Rq= qa |
|
q= const. |
||
0 |
|
|
||||
|
|
|
|
|
||
распределенной нагрузки, приложенная в |
|
|
|
|
|
|
|
|
|
|
|
||
центре тяжести её полосы загружения. |
|
|
|
|
|
|
|
|
|
|
|
||
Если q(ξ) = q = const, то Rq = qa и |
|
a/2 |
|
|
|
|
|
|
|
|
|||
приложена посередине полосы (рис. 1.2). |
|
|
|
a |
||
|
|
|
||||
Пары сил mi не имеют проекций на |
|
|
|
|||
|
|
|
|
|
||
координатные оси. |
Рис. 1.2. Равнодействующая |
|||||
Алгебраическая сумма моментов сил |
||||||
равномерно распределенной |
||||||
относительно моментной точки К в данном |
нагрузки |
|
|
|
||
случае будет :
∑MK = –F1r1 + F2r2 + F30 – Rqrq – m1 + m2 или при обратном правиле знаков
∑MK = F1r1 – F2r2 + F30 + Rqrq + m1 – m2.
Единицы измерения нагрузок таковы: Fi, Rqi – [кН], qi – [кН/м], mi – [кНּм].
1.2. Уравнения равновесия (статики) на плоскости
а) Если сосредоточенные силы Fi и равнодействующие Rqi распределенных нагрузок сходятся в одной точке (рис 1.3), то независимых уравнений равновесия здесь два: ∑FZ = 0, ∑FY = 0.
б) Для произвольной плоской системы сил (рис. 1.4) используют три эквивалентных варианта уравнений статики:
1)∑FZ = 0; ∑FY = 0; ∑MK = 0;
2)∑Mk1 = 0; ∑Mk2 = 0; ∑FY = 0 (или ∑FZ =0);
3)∑Mk1 = 0; ∑Mk2 = 0; ∑Mk3 = 0,
где моментные точки К1, К2, К3 не должны совпадать и в последнем случае не должны лежать на одной прямой.
|
y |
|
|
|
|
|
|
Rq3 |
F2 |
F3 |
y |
F1 |
|
F3 |
|
|
|
|
K3 |
||||
|
|
|
|
|
|
|
|
F1 |
|
Rq1 z |
m1 |
|
k1 |
|
Rq |
|
|
|
|
|
|
||
|
|
|
F2 |
|
K2 |
|
|
|
Rq2 |
|
|
m2 |
|||
|
|
|
|
|
|||
Рис. 1.3. Система сходящихся сил |
Рис. 1.4. Произвольная |
|
система сил |
||
|
5

q



 F2 z
F2 z
F1
Рис. 1.5. Нагрузки, лежащие на одной прямой
в) Если линии действия всех сил лежат на одной прямой, то рассматривают одно условие статики
(рис. 1.5): ∑FZ = 0.
1.3. Построение графиков (эпюр) элементарных функций
Многие расчеты в строительной механике сопровождаются построением различного вида графиков (эпюр). Напомним, как это делается для алгебраических функций одной независимой переменной. Например, построение эпюр внутренних усилий начинается с разбивки расчетной схемы конструкции на участки, на каждом из которых указывают пределы изменения независимой переменной. Такой участок в математике называется областью определения функции, в пределах которой и строят эпюру с указанием характерных значений (величины и знака) искомых ординат. В зависимости от выбранного начала отсчета независимой переменной (аргумента функции) указывают пределы её изменения на данном участке либо как а ≤ z ≤ b, либо как 0 ≤ z ≤ b. В последнем случае начало отсчета совмещают с началом участка, что удобнее.
Рассмотрим примеры. Пусть:
а) составлена функция ƒ1(z) = 4 с областью определения 0 ≤ z < 4,2. Её эпюра представлена на рис. 1.6, а. Очевидно, что если в выражение функции переменная z не входит, её значение на данном участке постоянно;
б) составлена функция ƒ2(z) = –3z+8 с областью определения 0 ≤ z ≤ 4. Так как функция содержит переменную z в первой степени, её эпюра есть прямая (линейная функция). Вычисляем концевые ординаты:
ƒ2(0) = 8; ƒ2(4) = –3·4 + 8 = –4. Эпюра ƒ2(z) представлена на рис. 1.6, б.
Абсцисса нулевой ординаты определяется из условия ƒ2(z0)= –3z0+8 = 0,
откуда z0 = 8/3 = 2,666;
в) составлена функция ƒ3(z) = –1,2 · z2 + 9,2 z – 4 с областью определения 0 ≤ z ≤ 6. Так как старшая степень переменной z равна 2, эта функция – парабола.
Эпюру ƒ3(z) строим по характерным точкам кривой, ординаты которых вычисляем так: в начале участка при z = 0, ƒ3(0) = –4; посередине участка при zср = 3 получаем ƒср = –1,2 · 32 + 9,2 · 3 – 4 = 12,8. Экстремальное
значение находим из условия равенства нулю первой |
производной от |
|||
ƒ3(z), что дает |
∂f3( z ) |
= −2,4zextr + 9,2 = 0, откуда zextr |
= |
9,2/2,4 = 3,833. |
∂z |
||||
Подставляя zextr |
в уравнение функции, получаем |
|
|
|
6 |
|
|
|
|
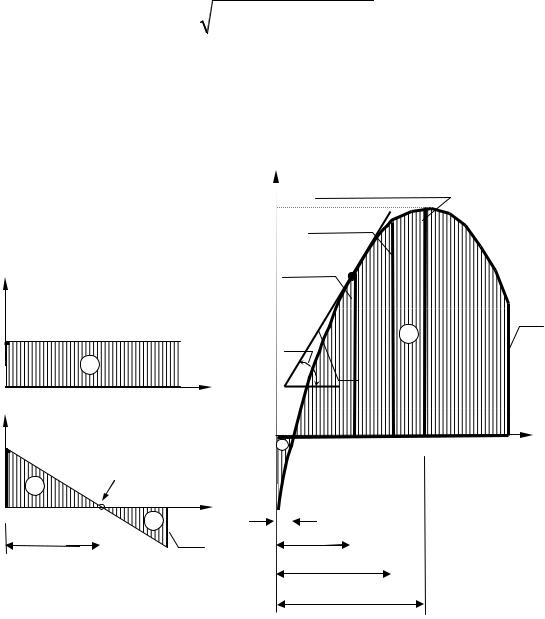
ƒ3max(3,833) = –1,2 · 3,8332 + 9,2 · 3,833 – 4 = 13,333. Концевая ордината при z = 6: ƒ3(6) = -1,2 · 62 + 9,2 · 6 – 4 = 8.
Положение нулевой ординаты находим из условия ƒ3(z0) = –1,2 z02 + 9,2 z0 – 4 = 0, откуда:
|
|
|
1 é |
|
|
|
|
|
ù |
|
-9,2 ± 8,09 |
|
|
|
|
|
|
|
|
2 |
|
|
|
||||
z0 |
= |
|
|
ê |
-9,2 |
± |
9,2 |
|
- 4 (-1,2) (-4)ú |
= |
-2, 4 |
, |
|
2 |
|
|
|||||||||||
|
|
(-1,2) ë |
|
|
|
|
û |
|
|
||||
а
4
0
б 8
0
|
|
z0(1) = − 9,2 + 8,09 |
= 0,462 |
и |
|
z0(2) = |
− 9,2 − 8,09 |
= 7,204 . |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
- 2,4 |
|
|
|
|
|
|
|
|
|
|
|
|
- 2,4 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ƒ3(z) |
|
|
|
Эпюраƒ3(z) |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
14 |
|
|
|
maxƒ =13,333 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ƒср=12,8 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ƒк=9,6 |
K |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ƒ1(z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Эпюраƒ1(z) |
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
φк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Касательная |
|
|
|
|
|
||||||||
1 |
|
2 |
|
3 |
|
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
ƒ2(z) |
Эпюраƒ2(z) |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
4 |
5 |
6 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ƒ2(z0)=0 |
z |
2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
4 |
4 |
|
|
|
|
|
Z0=0,462 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Z0=2,666 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
Zк =2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Zср |
=3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Zmax =3,833 |
|
|
|
|
|
|
|
||||||||
Рис. 1.6. Эпюры функций ƒi(z)
Первое значение z0(1) = 0,462 принадлежит участку, а второе z0(2)
выводит за пределы участка и должно быть отброшено. Эпюра ƒ3(z) показана на рис. 1.6, в. В заключение определим тригонометрические функции угла φК наклона касательной к кривой в точке К с абсциссой zК = 2 (рис. 1.6, в). Как известно, первая производная функции в декартовых
координатах равна тангенсу угла ϕК . Поэтому при zК = 2 имеем
7
tgjК = |
df3 (z) |
= -2,4 zК |
+ 9,2 = -2, 4×2 + 9,2 = 4,40. |
||||||||||
dz |
|||||||||||||
|
|
1 |
|
|
|
1 |
|
|
|
||||
Тогда cos jK |
= |
|
|
= |
|
= 0,2216 |
, а sinjK = tgjK × cos jK = |
||||||
|
|
|
|
|
|
|
|||||||
1+ tgϕ2 |
|
1+ 4,42 |
|||||||||||
|
|
|
K |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||
= 0,2216 · 4,4 = 0,9752, |
|
|
а |
sin2 ϕK + cos2 ϕK |
= 0,97522 + 0,22162 = 1. |
||||||||
1.4. Некоторые соотношения для плоских фигур
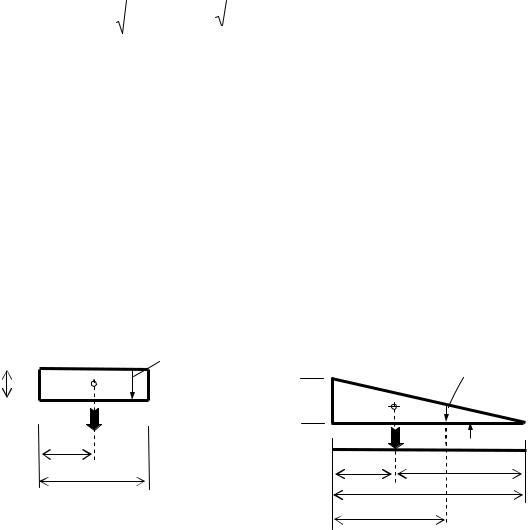
Прямоугольник (рис. 1.7). Площадь ω = hλ; если это полоса загружения равномерно распределенной (погонной) нагрузкой интенсивностью q0 = сonst, то на некоторых стадиях расчета сооружений ее представляют равнодействующей Rq = q0λ [кH], приложенной в центре С тяжести прямоугольника (zc = λ/2).
Прямоугольный треугольник (рис. 1.8). Площадь ω = 1/2 hλ; если это полоса загружения распределенной нагрузкой переменной интенсивности qz , то её равнодействующая Rq = q0 λ/2 и приложена в центре С тяжести с координатой zc = λ/3; tgα=h/λ.
) |
|
|
|
|
|
|
q0=const |
|
|
|
|
|
|
||
0 |
|
|
|
c |
|||
h(q |
|
|
|
|
Rq |
||
|
|
||||||
|
|
|
|||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
zc=λ/2 |
|||
|
|
|
|
|
|
λ |
|
Рис. 1.7. Прямоугольник |
|||||||
h(q0)
qz = q0 (λ − z )
c
λ
α
Rq
zc=λ/3 |
2 λ /3 |
λ
z
|
|
|
|
Рис. 1.8. Прямоугольный треугольник |
|
|||||||||||||
Трапеция (рис. 1.9). Площадь w = |
(h1 + h2) |
l ; если это полоса распре- |
||||||||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
(l - z) |
|
|
деленной нагрузки переменной интенсивности q |
z |
= q |
2 |
+ (q |
- q |
2 |
) |
, |
||||||||||
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
l |
|
||||
|
|
(q1 + q2) |
|
|
|
|
|
|
|
|
|
|
|
|||||
то ее равнодействующая Rq = |
l и приложена в центре С тяжести |
|||||||||||||||||
|
||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с координатой zc = |
(h1 + 2h2 ) λ |
º |
(q1 + 2q2 )λ |
|
. |
|
|
|
|
|
|
|
|
|
||||
3(h1 + h2 ) |
3(q1 |
+ q2 ) |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
8

Двузначная трапеция (рис. 1.10). Площадь w = |
(h1 + h2) |
l , где h2 < 0; |
|
2 |
|||
|
|
z0 |
= |
|
|
|
h1 |
|
|
|
l |
|
|
; здесь |
||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
h1 |
|
+ |
|
h2 |
|
|
||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||
Текущая ордината yz
qz = q2 + (q1
h1 , h2 принимать по абсолютной величине.
= h1 - (h1 + h2 ) lz .
- q2 )× |
(λ − z) |
1 |
|
|
yz |
h |
|
|
|
||
|
|
|
|||
|
|
|
|
||
l |
|
|
|
|
|
|
|
|
|
|
h1(q1)
c 
zc
z
 Rq
Rq
λ
h2(q2)
|
|
|
|
|
|
|
z |
|
|
|
h |
|
|
|
|
|
|
2 |
|
|
|
z0 |
|
|
|
||
|
|
|
|
|||
|
|
|
|
|||
|
a |
|
|
|
||
|
λ |
|
|
|
||
|
|
|
|
|
|
|
Рис. 1.10. Двузначная трапеция
Рис. 1.9. Трапеция
Полезно иметь в виду, что площади двузначных фигур в алгебраическом смысле могут быть равны нулю (например, здесь при h1 = h2 ). Но если бы определялась площадь ω фигуры для ее окраски,
то ее следовало бы вычислять арифметически w = |
h1 |
z0 |
+ |
h2 |
a |
. |
|
|
|
|
|||
2 |
2 |
|
||||
|
|
|
|
|||
1.5. О некоторых правилах приближенных вычислений
Реальные конструкции обычно несколько отличаются от их расчетных схем как величиной нагрузок, характеристиками материалов, так и размерами элементов. Поэтому так называемый «точный» расчет на самом деле таковым не является. В связи с этим выполняемые расчеты всегда более или менее приближенные, и стремление получать числовые результаты с большим количеством разрядов не оправдано. Не имеет смысла во всех случаях переписывать все, что появляется на индикаторе калькулятора. Сложились выработанные практикой некоторые правила обеспечения точности вычислений в разумных рамках.
Нужно сохранять в результатах лишь только верные значащие цифры. Нули, с которых начинаются числа, значащими не считаются. Но нули, стоящие в середине или в конце числа, удостоверяющие
9
отсутствие в числе единиц соответствующего разряда – цифры значащие. Например, в числе 0,003080 подчеркнутые нули слева значащими не считаются, остальные нули – значащие. Если значение какой-либо величины содержит лишние или недостоверные цифры, то его округляют. При этом правила округления таковы:
1)если первая отбрасываемая цифра больше 4, то последняя сохраняемая цифра увеличивается на единицу. Например, округляя число 51,5762 до сотых (здесь первая отбрасываемая цифра 6 > 4), принимаем 51,58;
2)если первая отбрасываемая цифра меньше или равна 4, то последняя сохраняемая цифра не изменяется. Если округляем до сотых число 51,5732, где первая отбрасываемая цифра не больше 4 (здесь 3 < 4), то принимаем 51,57;
3)если отбрасываемая часть числа состоит из одной цифры 5, то число округляют так, чтобы последняя сохраняемая цифра была четной. Например, округляя число 8,4375 до тысячных, принимаем 8,438, а если округляем число 8,345 до сотых, то принимаем 8,34;
4)при сложении и вычитании в результатах сохраняют столько десятичных знаков, сколько их имеет число с наименьшим количеством десятичных знаков;
5)при умножении и делении в результатах оставляют столько значащих цифр, сколько их имело приближенное число с наименьшим количеством значащих цифр;
6)расчет значений функций xn , n x, lg x приближенного числа x должен
x, lg x приближенного числа x должен
содержать столько значащих цифр, сколько их содержит само число x. При вычислении промежуточных результатов сохраняют на одну
цифру больше (запасную цифру), которая в окончательном результате отбрасывается.
2. КИНЕМАТИЧЕСКИЙ АНАЛИЗ СИСТЕМ
2.1. Виды систем
Расчетная схема сооружения получается из отдельных элементов, соединенных между собой и прикрепленных к земле. Совокупность всех элементов, связей между ними и связей элементов с землей будем называть системой. Различают три вида систем.
1. Геометрические неизменяемые системы – это такие системы, в
которых перемещения отдельных точек возможны только при деформировании некоторых элементов. Например, в системе, показанной на рис. 2.1, а, узел А может перемещаться только в том случае, если прикрепляющие его к земле стержни АВ и АС будут деформироваться.
10
