1.10.4. Метод Гаусса (метод исключения).
Этот метод применяется к системам уравнений самого общего вида (1.6) и основан на использовании элементарных преобразований над строками расширенной матрицы. Эта матрица для системы (1.6) имеет вид:
.
С помощью элементарных
преобразований над строками матрица
приводится к «ступенчатому» виду (прямой
ход метода Гаусса). В ходе этого приведения
получающиеся нулевые строки вычеркиваются.
При этом одновременно решается вопрос
о совместности системы – если первыеn
элементов какой-либо строки матрицы
(соответствующие элементам исходной
матрицыA)
оказались нулевыми, а последний элемент
этой строки (правая часть) ненулевой,
то это означает, что система (1.4) является
несовместной. Действительно, в этом
случае имеет место уравнение
,
не имеющее решения.
Далее, в полученной «ступенчатой»
матрице в ее первых столбцах следует
расположить базисный минор с верхней
треугольной матрицей. Обычно он получается
автоматически в процессе прямого хода,
но иногда для этого может понадобиться
перестановка столбцов. На этом прямой
ход метода Гаусса заканчивается. Для
«ступенчатой» матрицы строится
укороченная система уравнений, в правую
часть которой переносится последний
столбец расширенной матрицы, а также
все столбцы, не вошедшие в базисный
минор (с противоположным знаком). Затем
полученная укороченная система решается
последовательной подстановкой, начиная
с последней строки, что является обратным
ход метода Гаусса, в результате которого
находятся искомое решение системы
(1.4), то есть все компоненты вектора
.
Пример.
Найти решение системы:
.
Решение. Выпишем расширенную матрицу и с помощью элементарных преобразований приведем ее к «ступенчатому» виду:
.
Переставляя в последней матрице второй и третий столбцы, запишем укороченную систему с верхней треугольной матрицей:
,
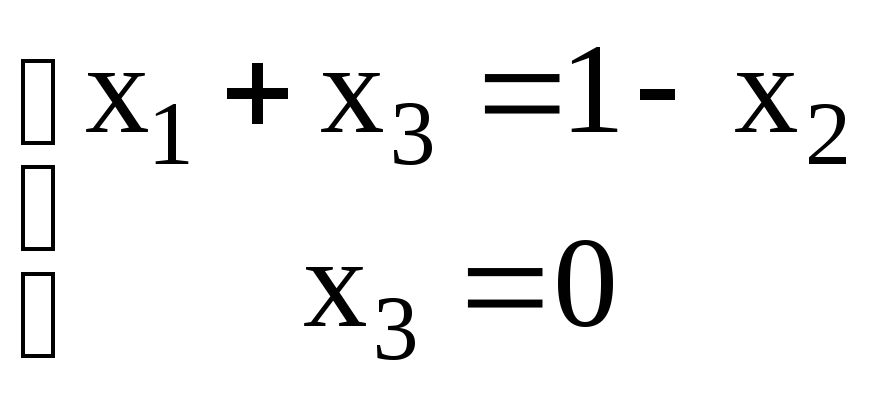решением которой является вектор
или
,
где первый столбец
является частным решением неоднородной
системы, второй – фундаментальным
решением однородной системы, соответствующей
данной неоднородной,
– произвольная постоянная.
1.11. Задачи
1. Решить систему
уравнений с помощью обратной матрицы
и методом Крамера:
.
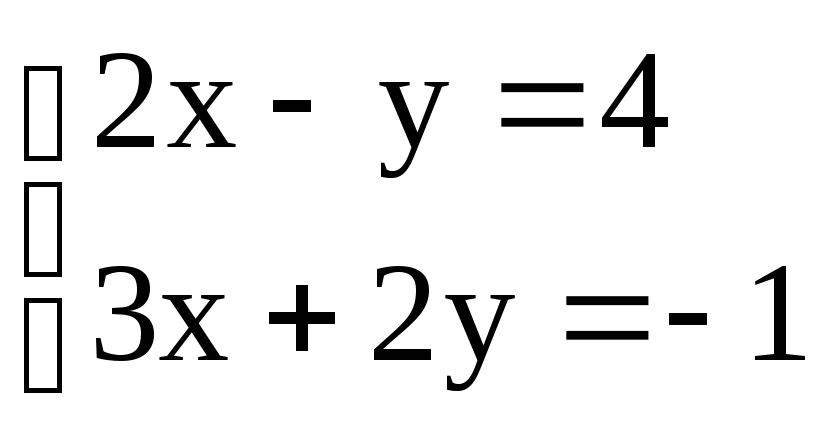Решить системы уравнений методом Крамера:
2.
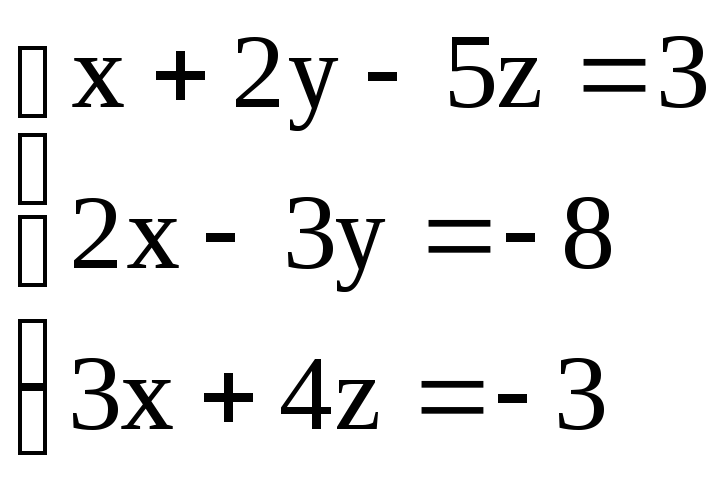. 3.
.
Решить системы уравнений методом Гаусса:
4.
.
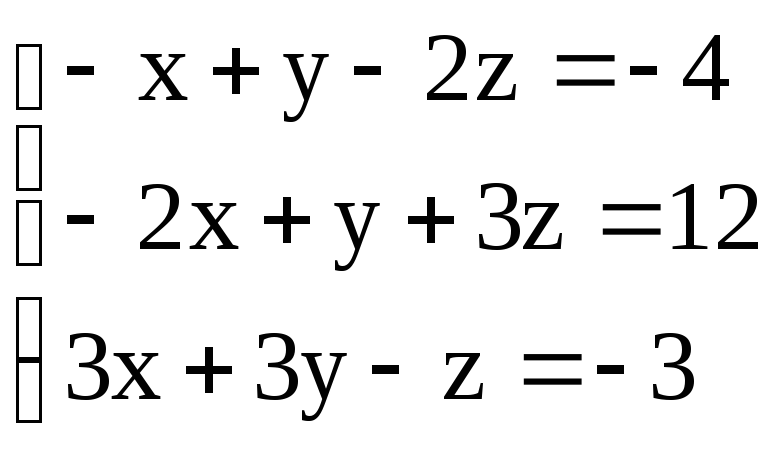5.
.
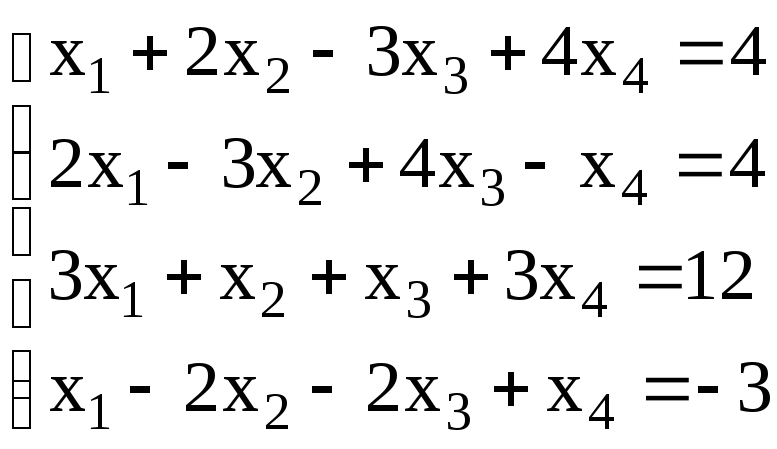6.
.
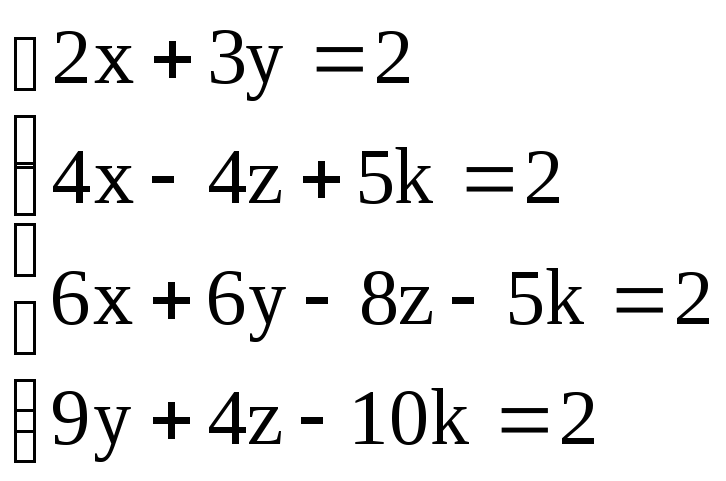Исследовать однородную систему уравнений. В случае существования нетривиального решения найти фундаментальную систему решений и общее решение системы:
7.
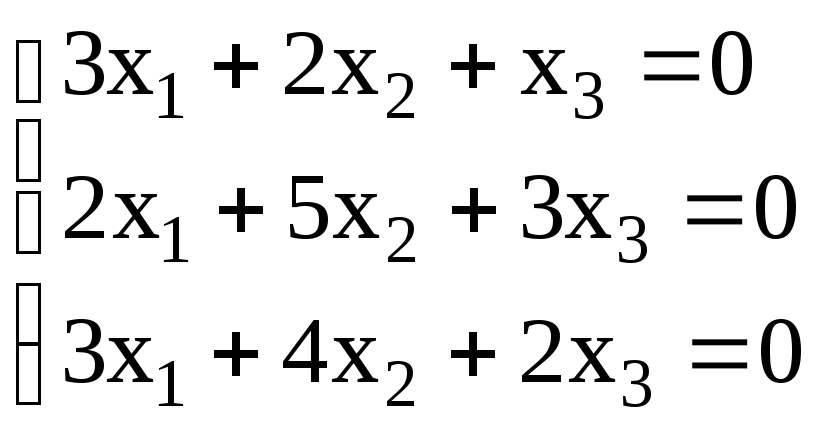. 8.
.
9. Определить
значение
,
при котором система имеет нетривиальное
решение, найти это решение:
.
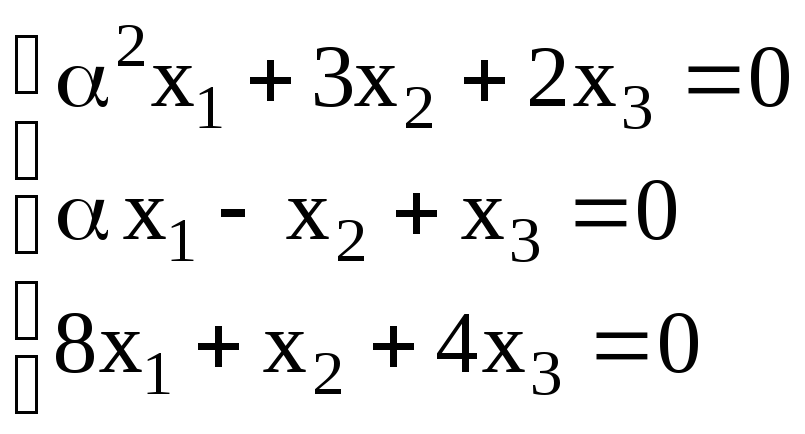Исследовать неоднородную систему уравнений. В случае совместности найти решение и представить его через фундаментальную систему решений соответствующей однородной системы:
10.
.
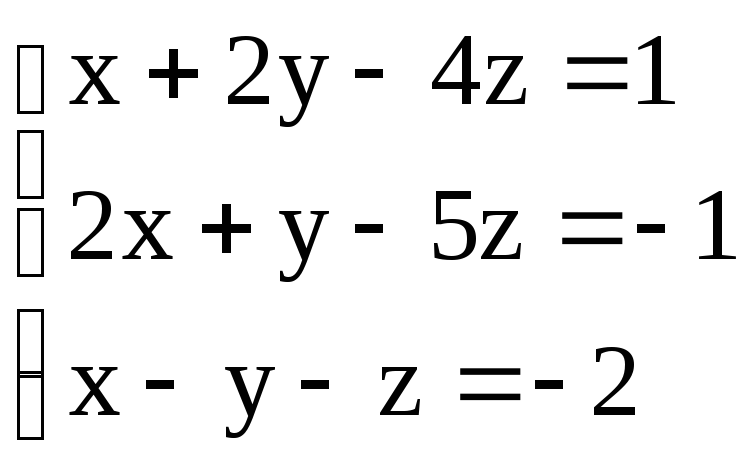11.
.
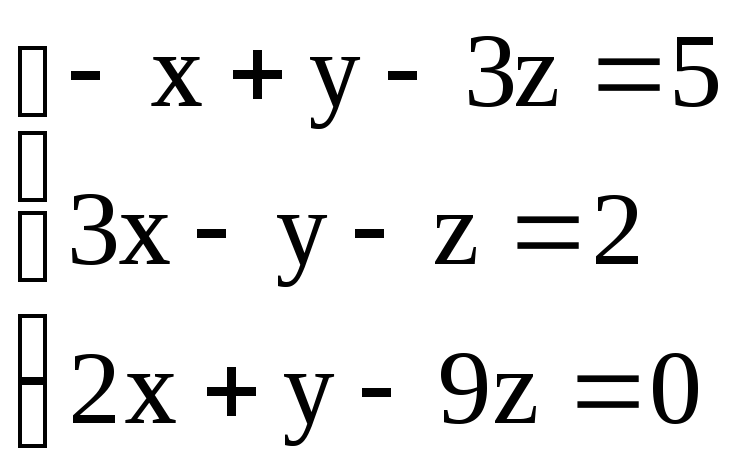12.
.
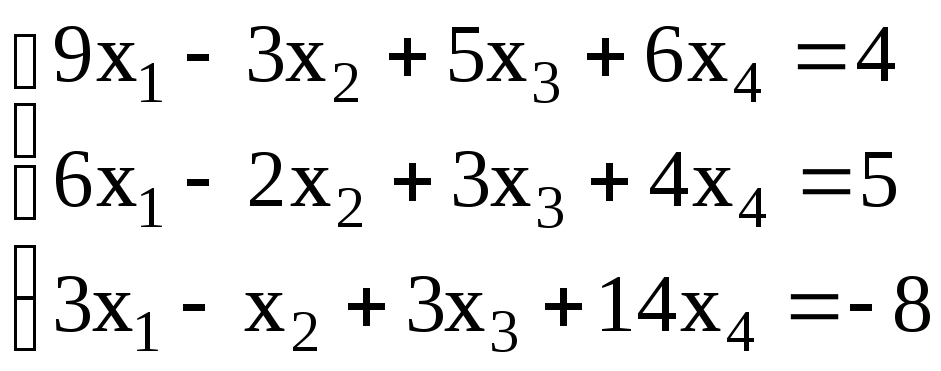Домашнее задание.
Решить системы уравнений методом Крамера и с помощью обратной матрицы:
13
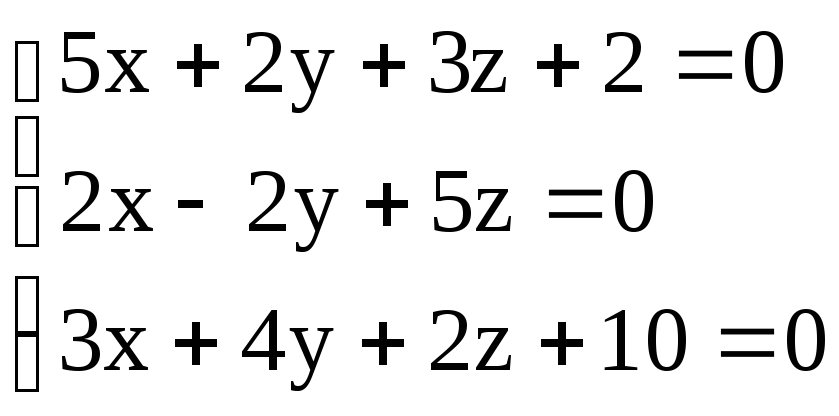. 14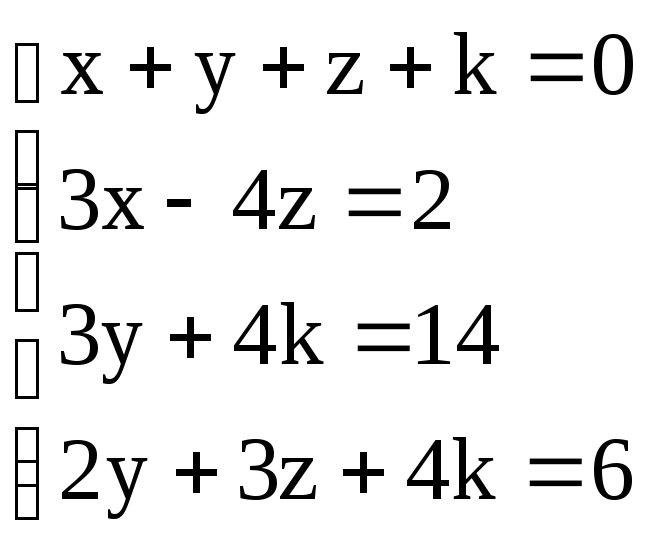
.
Решить системы уравнений методом Гаусса:
15
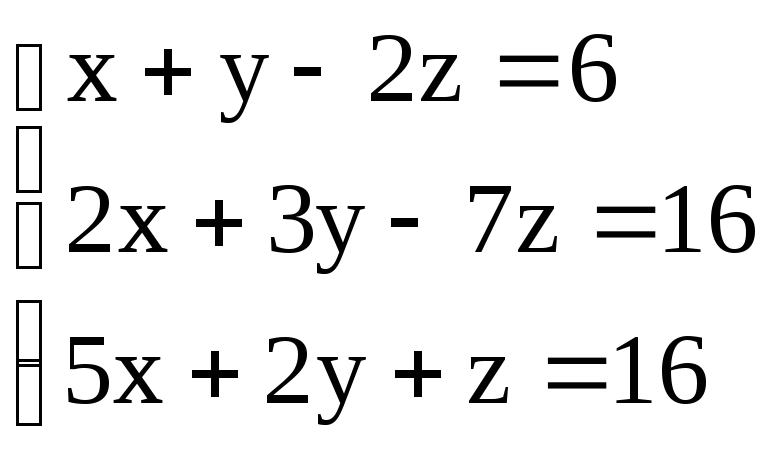. 16.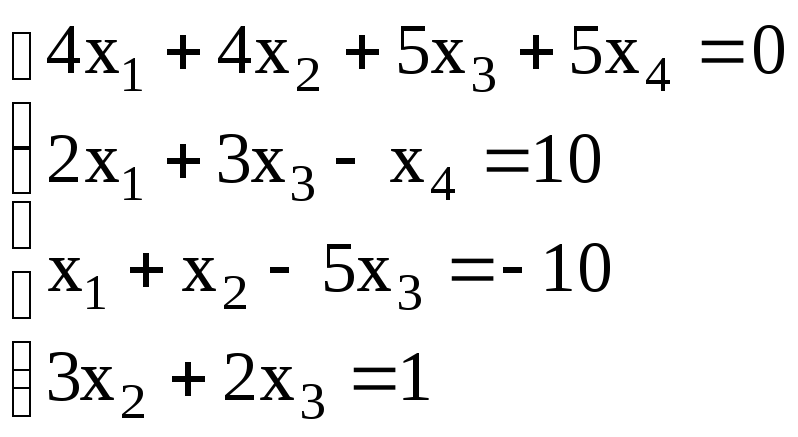
.
Решить систему однородных уравнений. В случае существования нетривиального решения найти фундаментальную систему решений и общее решение системы:
17.
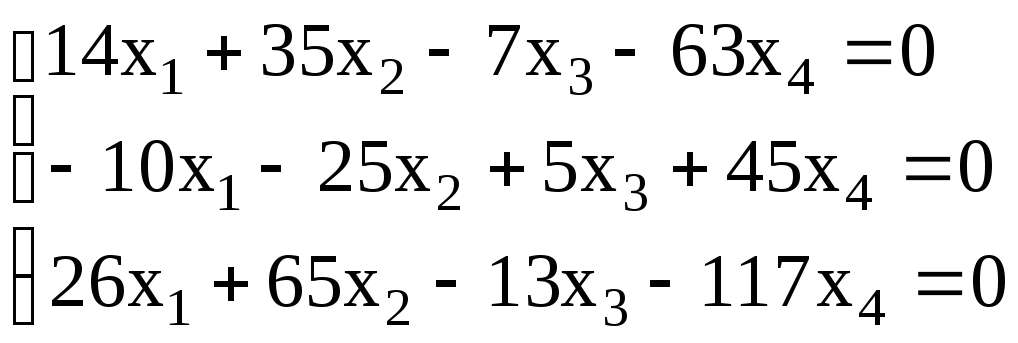. 18.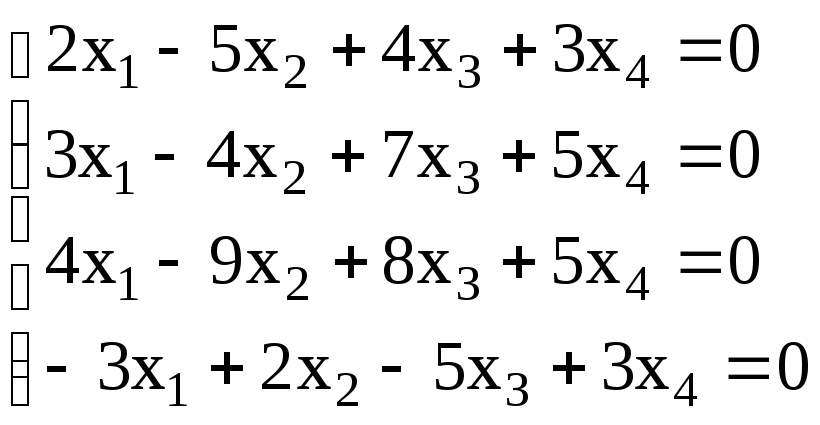
.
19. Определить
значение
,
при котором система имеет нетривиальное
решение, найти это решение:
.
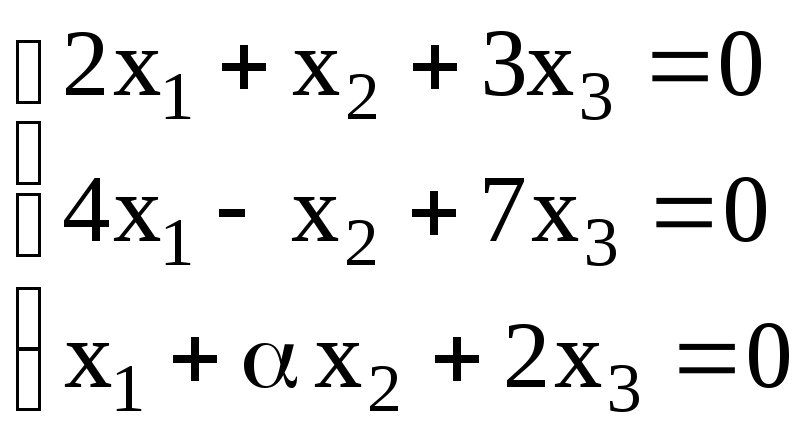Решить неоднородную систему уравнений. В случае совместности найти решение и представить его в виде суммы частного решения и фундаментальных решений соответствующей однородной системы:
20.
. 21.
.
Ответы. 1. (1;-2). 2. (-1;2;0). 3. (3;1;2;-1). 4. (-1;1;3). 5. (3;2;1;0).
6.
.
7. (2;-3;-2). 8. (-2;2;-2;2). 9. (3;1;-1). 10.
(1;-1;2;-2).
11. Только тривиальное решение.
12.
+
.
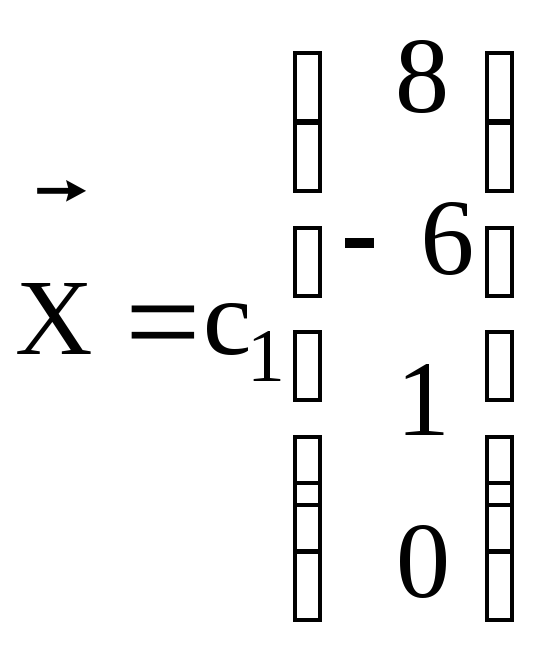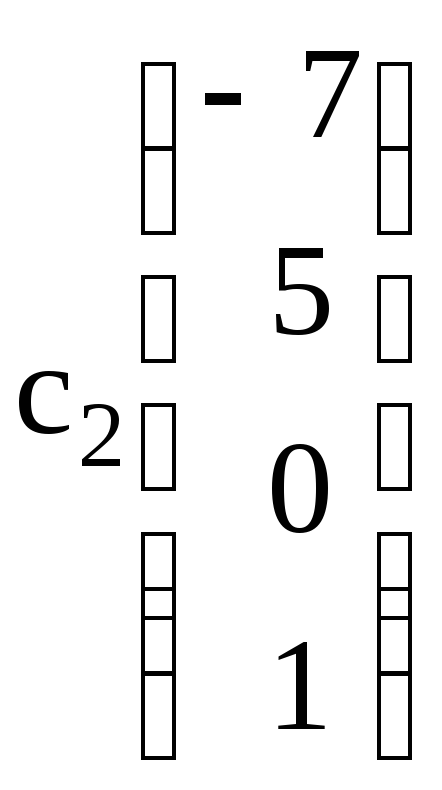13.
,
;
,
.
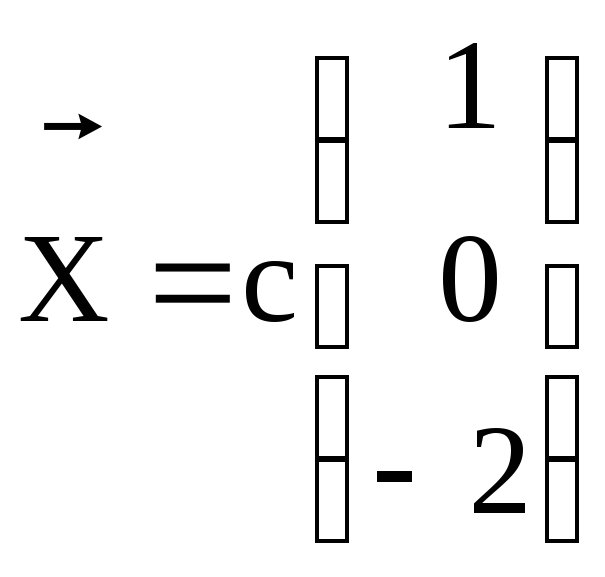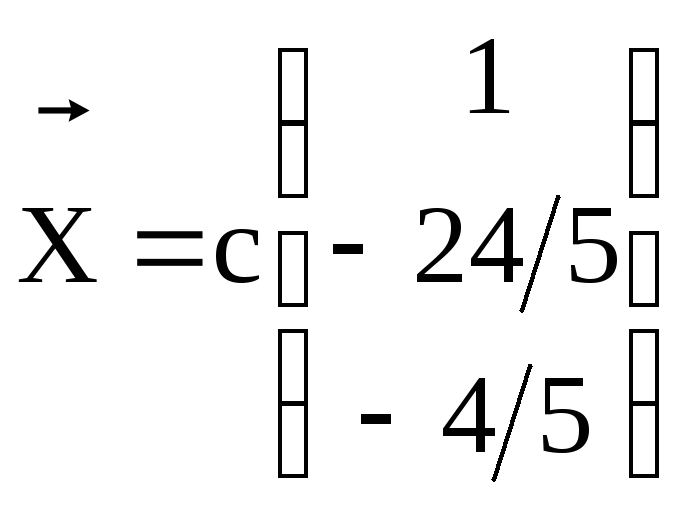14.
.
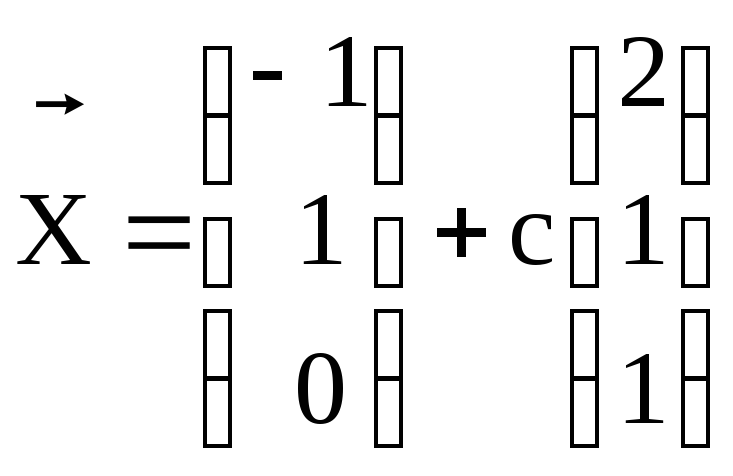15. Несовместная.
16.
.
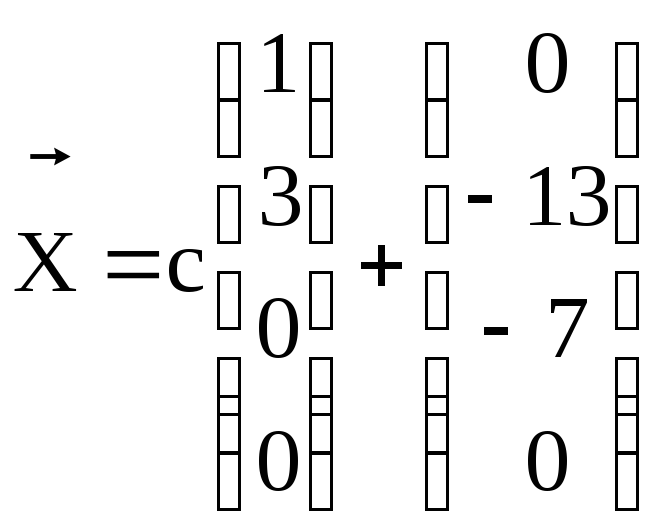17.
+
+
.
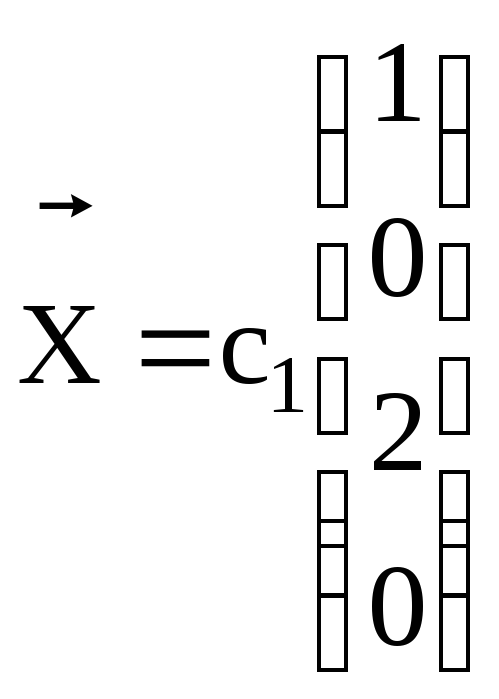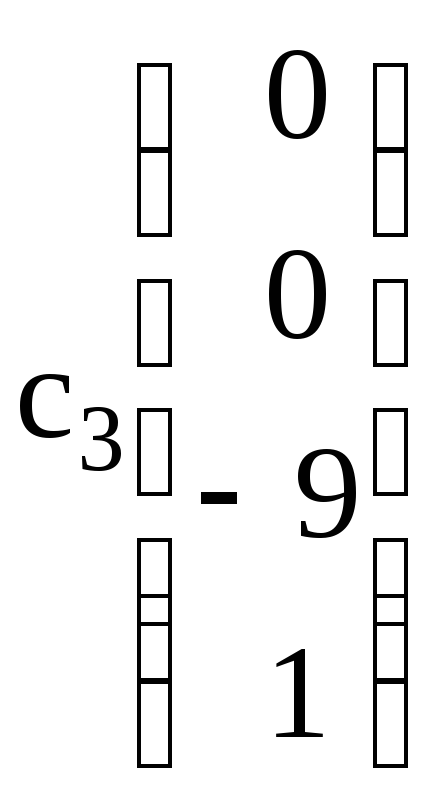18. Только тривиальное
решение. 19.
,
.
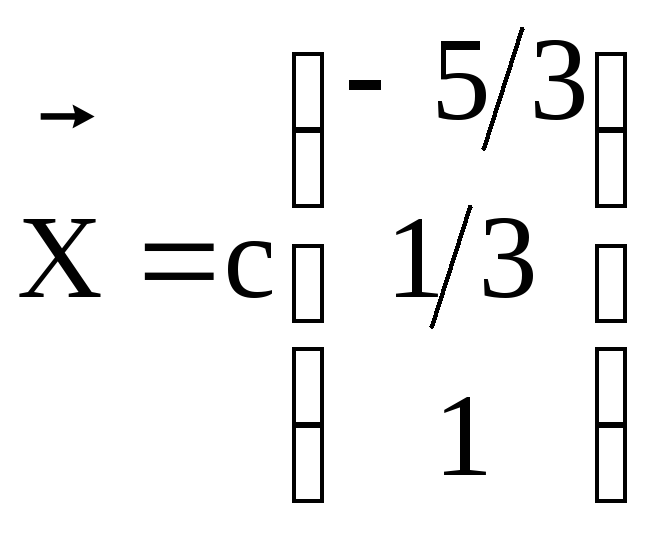20. Несовместная.
21. Совместная,
неопределенная,
.
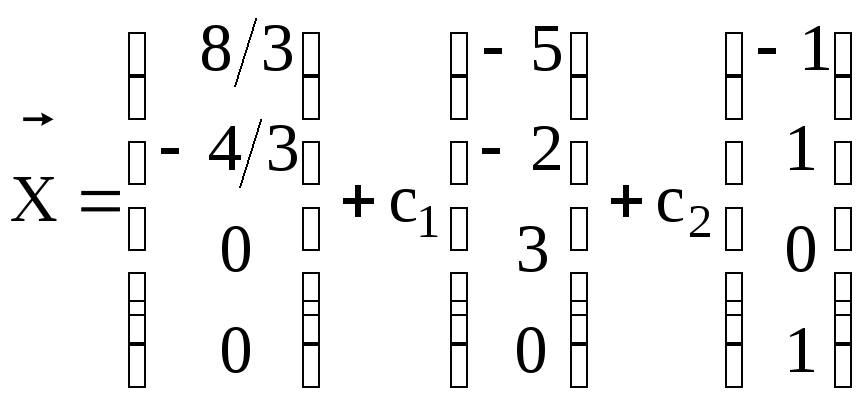