
- •Глава 1. Алгебра матриц и линейные алгебраические уравнения
- •Матрицы.
- •1.1. Свойства матриц.
- •1.1.1. Некоторые свойства квадратных матриц.
- •1.2. Блочные матрицы
- •Например, матрицу
- •1.3. Задачи
- •Домашнее задание.
- •1.4. Определители.
- •1.4.1. Основные свойства определителей.
- •1.4.2. Способы вычисления определителей.
- •1.5. Задачи
- •Домашнее задание.
- •1.6. Обратная матрица.
- •1.7. Задачи
- •Домашнее задание.
- •1.8. Ранг матрицы.
- •1.8.1. Вычисление ранга матрицы.
- •1.9. Задачи
- •Домашнее задание.
- •1.10. Системы линейных алгебраических уравнений (слау).
- •1.10.1. Системы уравнений с квадратной матрицей.
- •1.10.2. Однородные системы.
- •1.10.3. Системы уравнений общего вида.
- •1.10.4. Метод Гаусса (метод исключения).
- •1.11. Задачи
- •Домашнее задание.
1.5. Задачи
Вычислить определители второго порядка:
1.
![]() . 2.
. 2.![]() .
.
3. Вычислить определитель третьего порядка по правилу треугольников:
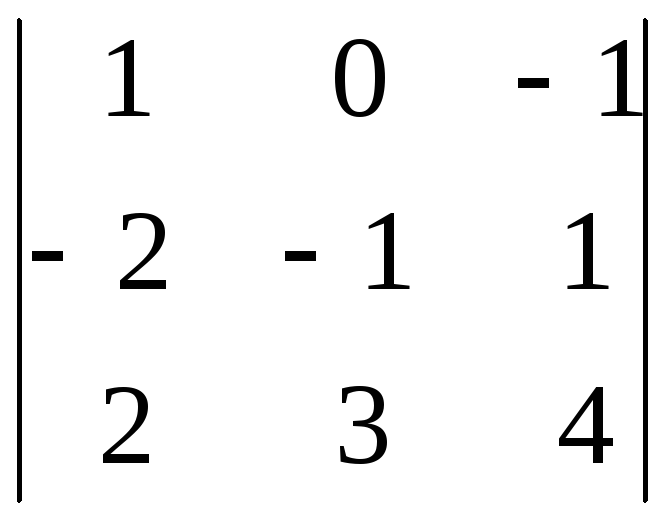 .
.
Вычислить определители с помощью разложения по строке или столбцу:
4.
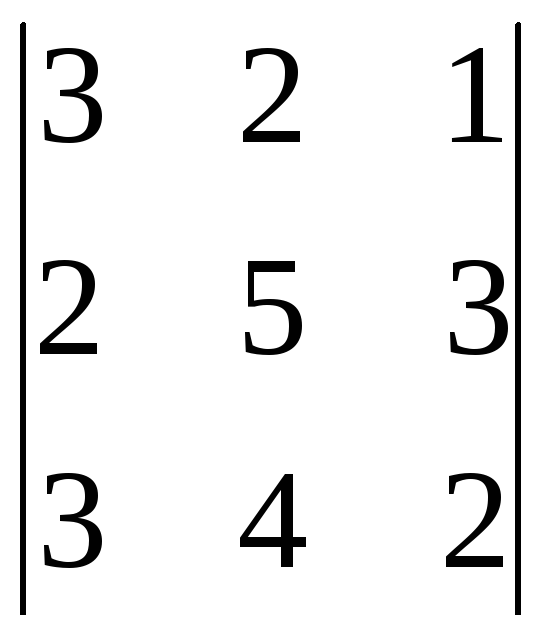 . 5.
. 5.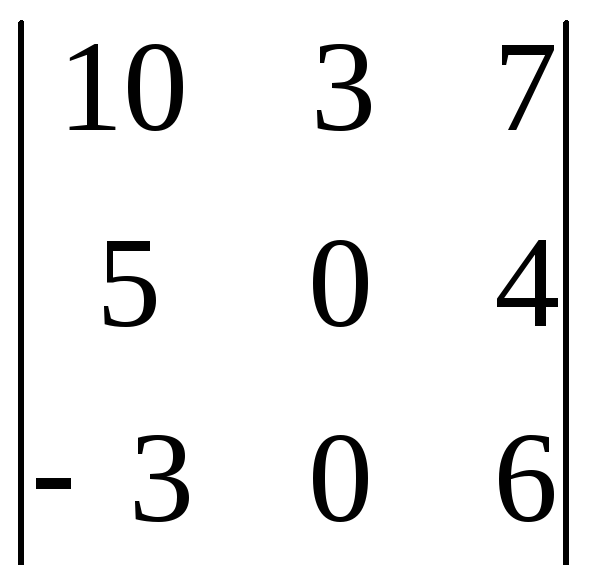 . 6.
. 6. .
.
Вычислить, используя свойства определителей:
7.
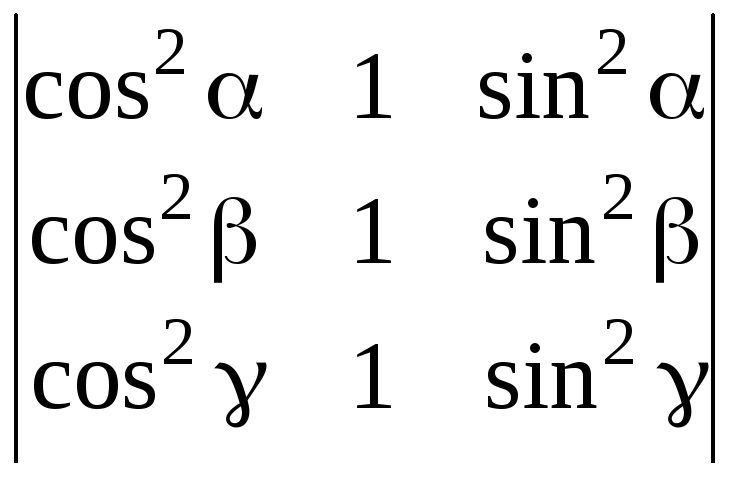 . 8.
. 8. .
.
9.
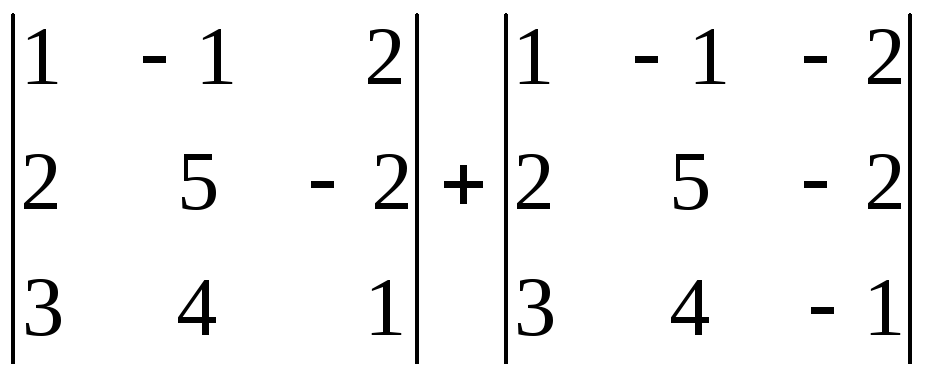 . 10.
. 10.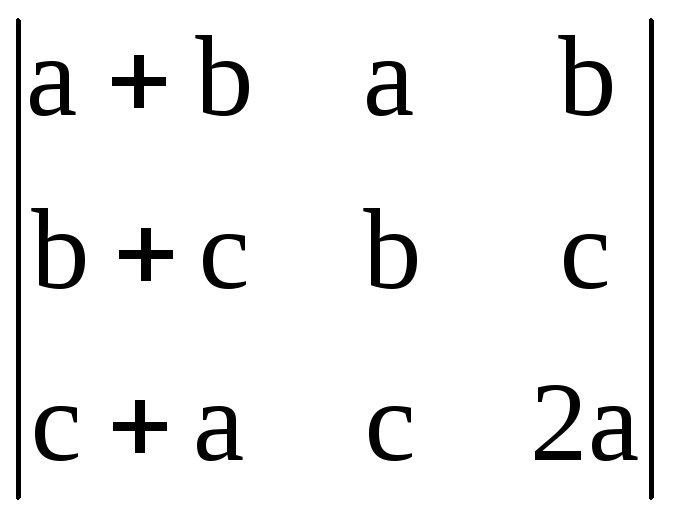 .
.
11. Используя свойства определителя, доказать тождество:
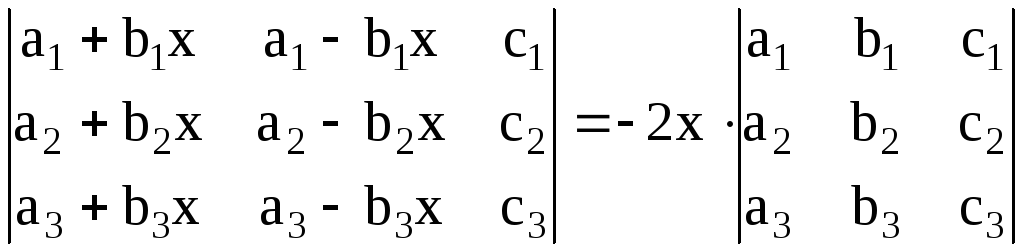 .
.
12. Решить уравнение:
 .
.
Домашнее задание.
Вычислить:
13.
![]() .
14.
.
14.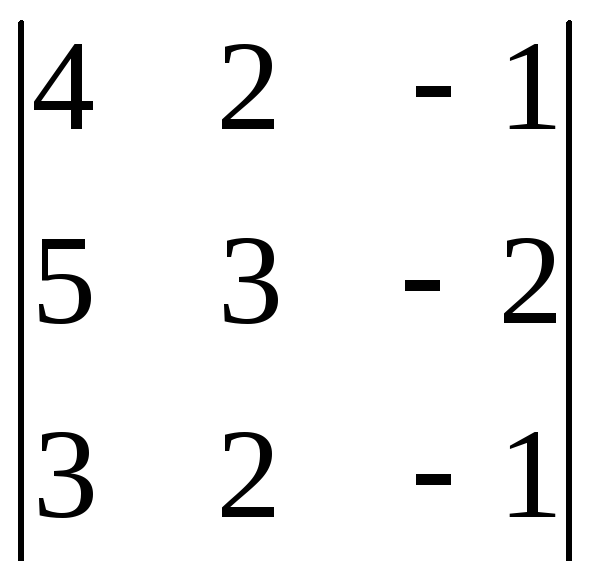 .
15.
.
15.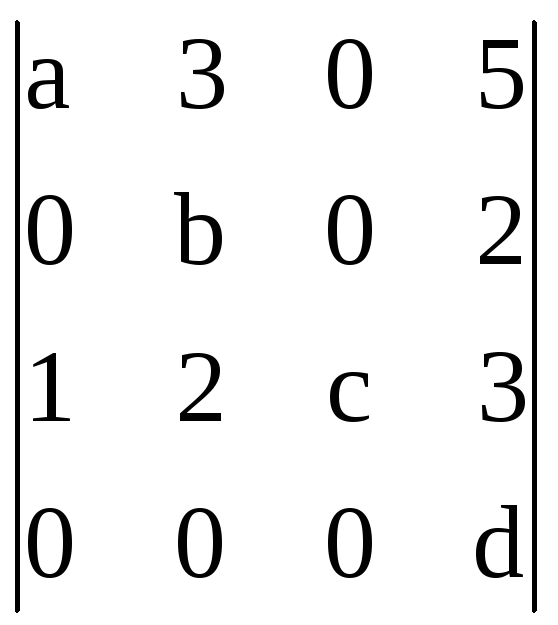 .
16.
.
16. .
.
Вычислить, используя свойства определителей:
17.
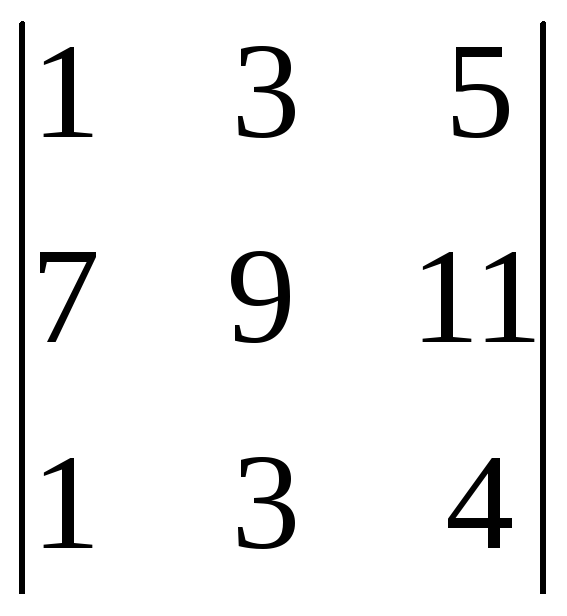 .
18.
.
18.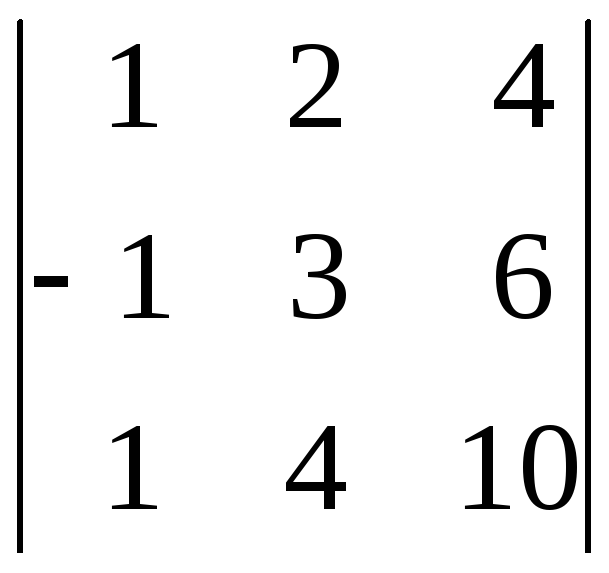 .
19.
.
19. .
.
20.
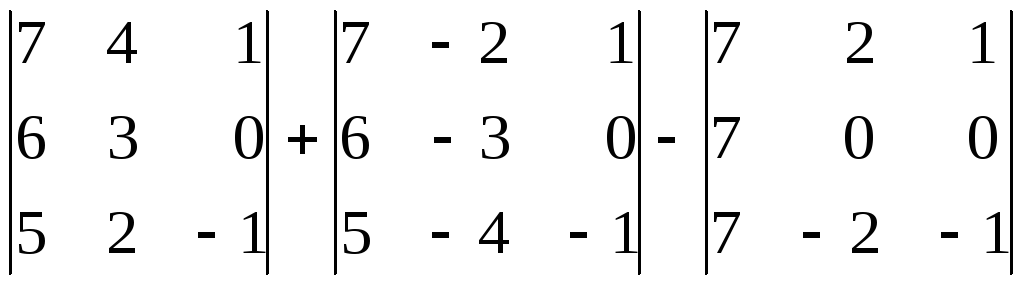 .
.
Решить уравнения:
21.
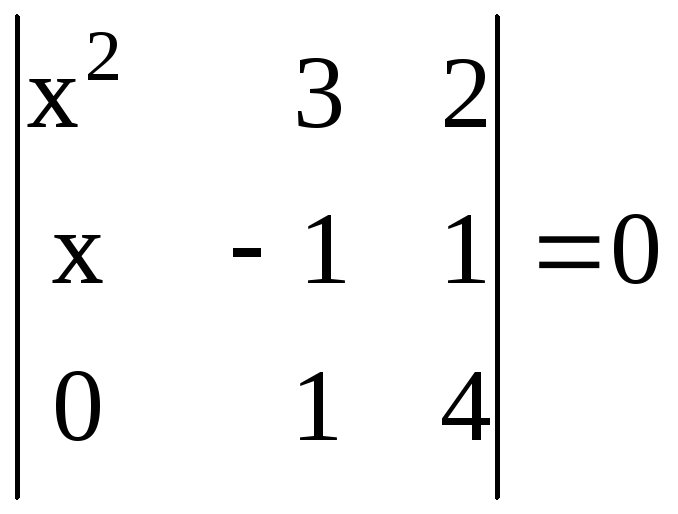 . 22.
. 22.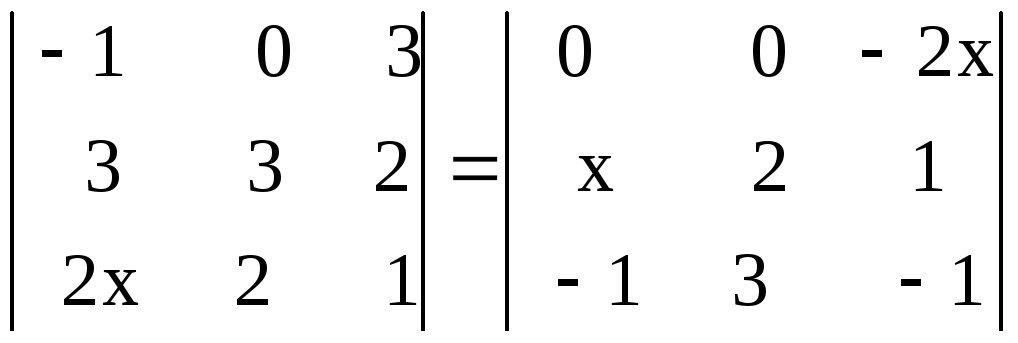 .
.
Ответы.
1. 15. 2.
![]() .
3. -3. 4. -3. 5. -126. 6. 216. 7. 0. 8. 180.
.
3. -3. 4. -3. 5. -126. 6. 216. 7. 0. 8. 180.
9. 28. 10.
![]() .
12.
.
12.![]() .
13. 13. 14. 1. 15.
.
13. 13. 14. 1. 15.![]() .
16. 120.
.
16. 120.
17. 12. 18. 10. 19. 0.
20. 0. 21.
![]() .
22.
.
22.![]()
1.6. Обратная матрица.
Пусть А - квадратная матрица n-го порядка и Е - единичная матрица того же порядка. Матрица В называется обратной по отношению к матрице А, если
![]() .
.
Легко показать,
что
![]() .
Действительно,
.
Действительно,
![]() .
.
Отсюда следует,
что
![]() .
.
Покажем, что определенная таким образом обратная матрица является единственной. Действительно, пусть С и В - две различные обратные матрицы по отношению к А. Тогда по определению
![]() и
и
![]() .
.
Вычтем из первого равенства второе
![]() .
Получили, что
.
Получили, что
![]() ,
значит
,
значит![]() ,
то есть В = С.
,
то есть В = С.
Обратная матрица
обозначается
![]() ,
где
,
где![]() не
степень, а символ. Таким образом,
не
степень, а символ. Таким образом,
![]() .
.
Следующая теорема определяет условия существования обратной матрицы.
Теорема. Для того, чтобы у матрицы А существовала обратная матрица, необходимо и достаточно, чтобы определитель матрицы А был отличен от нуля.
Доказательство.
1) Необходимость.
Если
![]() существует, то по свойству 7 определителей:
существует, то по свойству 7 определителей:
![]() ,
откуда следует, что
,
откуда следует, что
![]() .
.
2) Достаточность.
Пусть
![]() .
Составим матрицу В из алгебраических
дополнений матрицы А, расположенных по
столбцам, то есть матрицу вида
.
Составим матрицу В из алгебраических
дополнений матрицы А, расположенных по
столбцам, то есть матрицу вида
 .
.
Составим произведение
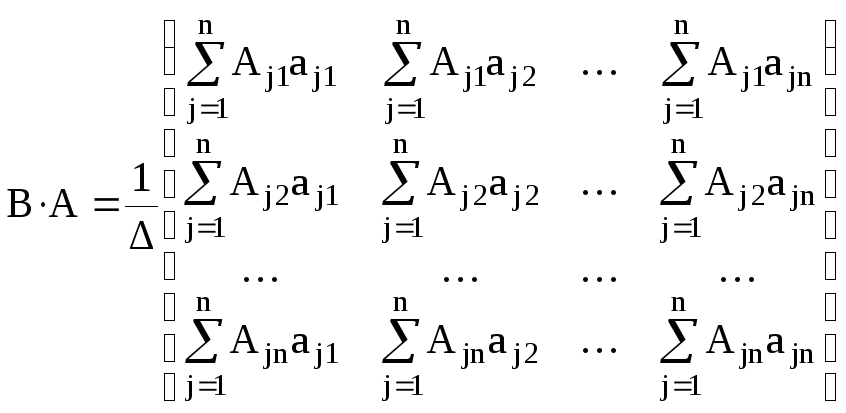 .
.
Тогда
![]() ,
поскольку все внедиагональные элементы
данной матрицы равны нулю как разложения
по «чужой» строке. Таким образом, матрица
В является обратной по отношению к
матрице А. Теорема доказана.
,
поскольку все внедиагональные элементы
данной матрицы равны нулю как разложения
по «чужой» строке. Таким образом, матрица
В является обратной по отношению к
матрице А. Теорема доказана.
При доказательстве теоремы был также получен алгоритм построения обратной матрицы:
1) Вычисляется
![]() ;
;
2) Составляется
матрица из алгебраических дополнений
матрицы А, записанных по столбцам,
которая называется присоединенной
матрицей
матрицы А и обозначается как
![]() .
Таким образом,
.
Таким образом,![]() ;
;
3) Строится обратная
матрица, которая имеет вид:
![]() .
.
Описанный алгоритм построения обратной матрицы называется методом присоединенной матрицы.
Существует и другой способ построения обратной матрицы, не требующий вычисления определителей, что существенно при построении обратных матриц больших размерностей.
Рассмотрим матричное
уравнение
![]() ,
решением которогоX
и является обратная матрица, т.е.
,
решением которогоX
и является обратная матрица, т.е.
![]() .
Для ее нахождения применяется метод
последовательного исключения (метод
Гаусса), который подробно рассматривается
в п. 1.5, поэтому изложим только способ
его применения.
.
Для ее нахождения применяется метод
последовательного исключения (метод
Гаусса), который подробно рассматривается
в п. 1.5, поэтому изложим только способ
его применения.
Составим из матриц А и Е расширенную прямоугольную матрицу, дописывая справа к каждой строке матрицы А соответствующую строку единичной матрицы Е.
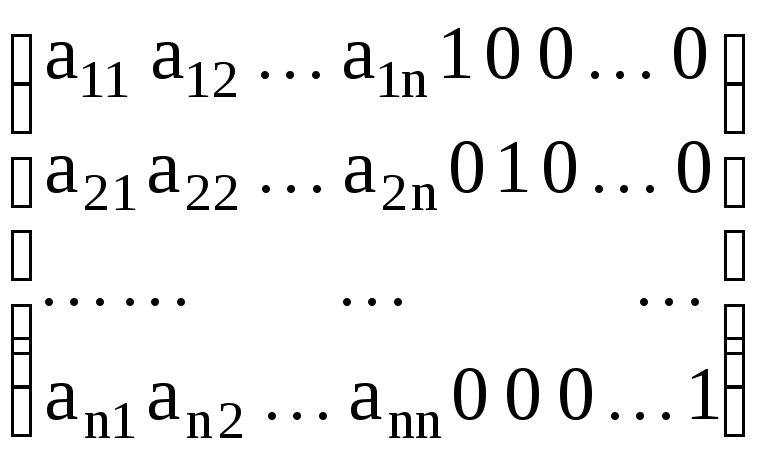 .
.
С помощью элементарных преобразований над строками этой матрицы, как это было описано в п. 1.2.2, преобразуем так левую часть этой матрицы, чтобы на том месте, где была расположена матрица А, оказалось единичная матрица. Тогда на том месте, где находилась единичная матрица, окажется искомая обратная матрица. Этот способ также легко алгоритмизуется и может быть реализован на ЭВМ для вычисления обратной матрицы любой размерности.
