1.10.1. Системы уравнений с квадратной матрицей.

Решение вопроса об определенности и неопределенности системы начнем с рассмотрения систем вида (1.6) с квадратной матрицей, то есть когда n = m:

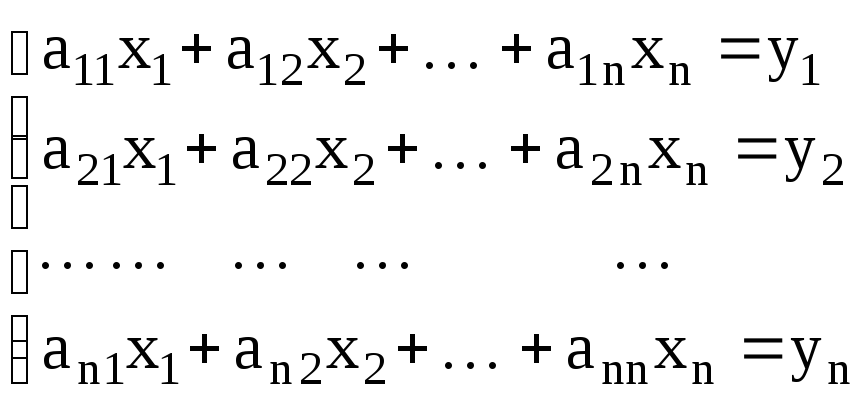(1.7)

или в матрично-векторном виде .

В том случае, если у матрицы А существует обратная матрица, решение системы (1.7) находится сразу: . При этом имеет место следующая теорема.

Теорема. Если определитель системы (1.7) не равен нулю, то система (1.7) имеет единственное решение для любого вектора , вычисляемое по формулам Крамера:

,

где - определитель, получаемый из определителя, в котором числаj-го столбца заменены на компоненты вектора .

Доказательство. Решение системы (1.7) запишем в виде , а обратную матрицу вычислим через присоединеннуюили:

,

откуда следует равенство

,

что совпадает с разложением определителя поj - му столбцу, если элементы этого столбца заменить на элементы вектор- столбца правых частей системы (1.7). Следовательно,

.

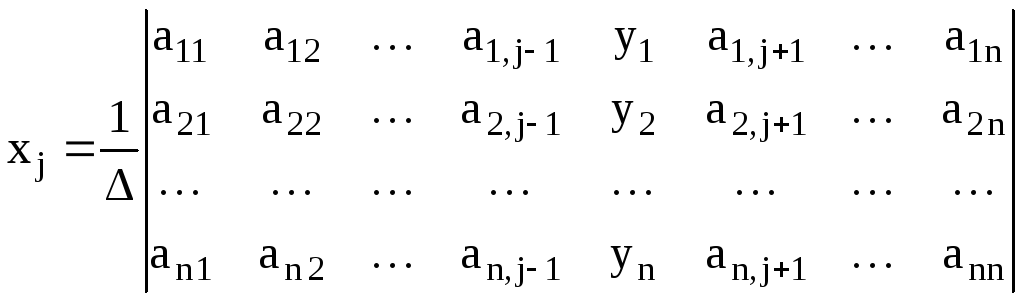Теорема доказана.

1.10.2. Однородные системы.

Система уравнений

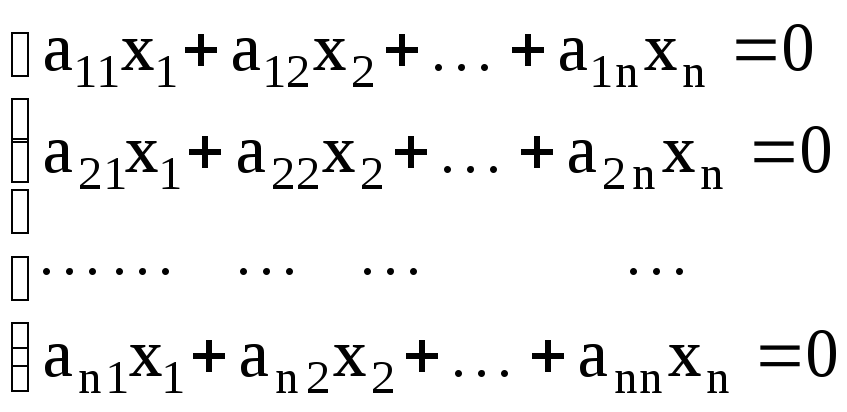(1.8)

с нулевой правой частью называется однородной.

Для системы (1.8) всегда выполняется условие и она всегда совместна. Ясно, что нулевой векторилиявляется ее решением при любых значениях коэффициентовматрицы А и его называюттривиальным решением системы (1.8).

Теорема. Если определитель однородной системы не равен нулю, то эта система имеет только тривиальное решение.

Доказательство. Поскольку в системе (1.8) , а по условию теоремы, то по формулам Крамераи, то есть. Теорема доказана.

Следствие. Для существования нетривиального решения однородной системы необходимо и достаточно, чтобы ее определитель был равен нулю.

1.10.3. Системы уравнений общего вида.

Рассмотрим теперь неоднородную систему линейных уравнений общего вида, когда матрица А системы (1.6) является прямоугольной, то есть . Будем предполагать, что система совместна и хотя бы один элемент матрицы А отличен от нуля. Тогда. Не ограничивая общности, можем предположить, что базисный минор матрицы А находится в левом верхнем углу этой матрицы. Этого всегда можно добиться путем перестановки строк расширенной матрицы и столбцов основной, перенумеровывая при этом компоненты искомого вектора. Таким образом, пусть мы имеем систему:

.

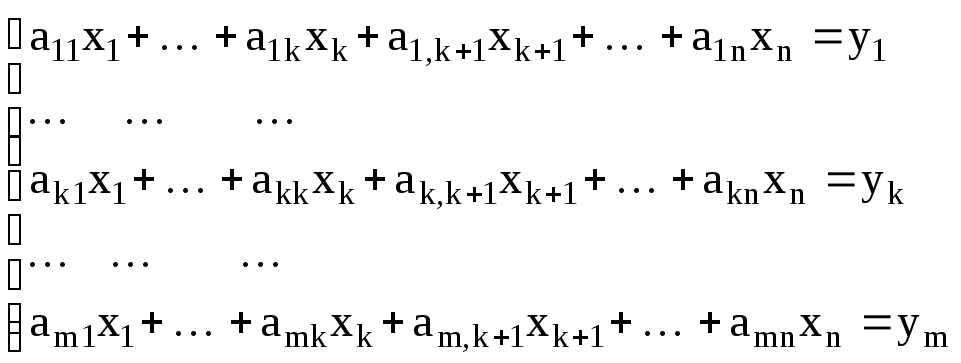Тогда первые k строк как основной, так и расширенной матриц по теореме о базисном миноре являются линейно – независимыми базисными строками, а остальные (m-k) строк, начиная с k+1 –ой, являются линейными комбинациями базисных строк. Это означает, что каждое из уравнений данной системы, начиная с k+1 –го, является линейной комбинацией (следствием) первых k уравнений этой системы, то есть всякое решение первых k уравнений системы обращает в тождество и все последующие уравнения этой системы. Поэтому достаточно найти все решения лишь первых k уравнений, отбросив все остальные. Назовем неизвестные , входящие в базисный минор,базисными, а остальные –свободными. Перенесем слагаемые, содержащие свободные переменные, в правую часть и запишем «укороченную» систему, полностью эквивалентную исходной, в следующем виде:

.

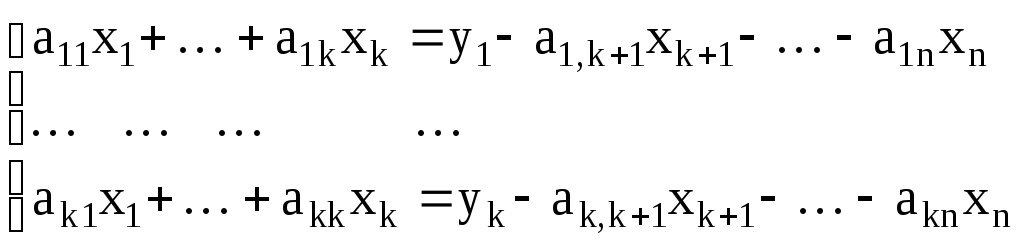Придадим свободным переменным произвольные числовые значения и запишем решение укороченной системы по формулам Крамера ():

,

где и все остальные, есть вектор – столбцы соответствующих коэффициентов матрицы А. По свойству (8) определителя, если столбец состоит из суммы каких-либо других столбцов, то имеем:

,

что и является общим решением системы неоднородных уравнений (1.4) с прямоугольной матрицей. Заметим, что величины есть числа, определяемые только правой частью и коэффициентами матрицы. Перенумеруем для удобства произвольные постоянные:,и так далее. Тогда получим:

.

Можно утверждать, что общее решение неоднородной системы содержит произвольные постоянные, число которых равно разности между числом неизвестных и рангом матрицы системы.

Рассмотрим некоторые частные случаи.

1. Ранг матрицы А равен числу неизвестных (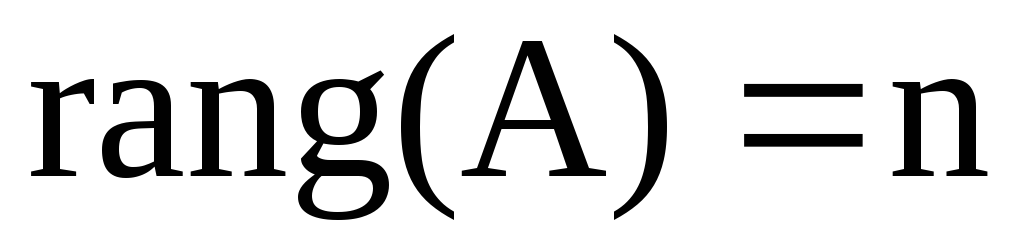). В этом случае

,

общее решение не содержит произвольных постоянных и является единственным решением системы.

2. Система является однородной, то есть 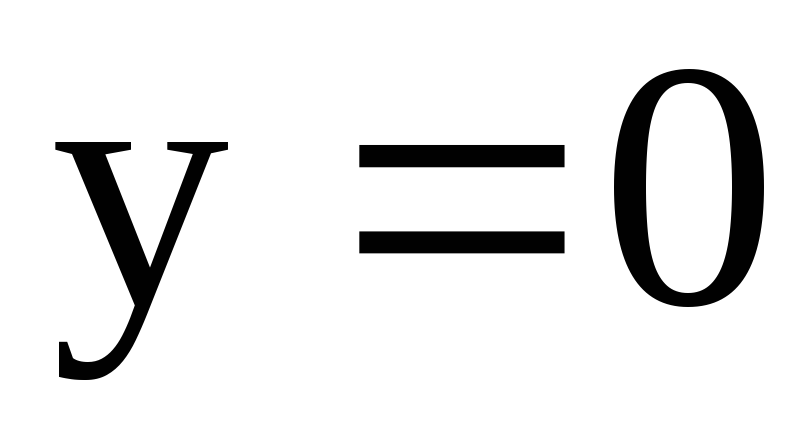. В этом случае

или в векторном виде

.

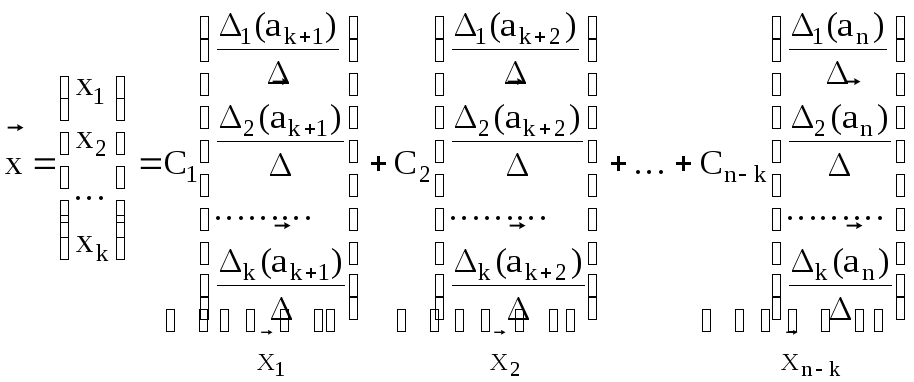Векторы- столбцы в правой части зависят только от коэффициентов матрицы А и называются фундаментальными решениями однородной системы. Их совокупность называетсяфундаментальным решением однородной системы. Тогда общее решение однородной системы является линейной комбинацией этих фундаментальных решений

.

Для неоднородной системы уравнений фундаментальной совокупности решений нет из-за наличия правой части. Однако имеет место следующее утверждение.

Утверждение. Сумма частного решения неоднородной системы и общего решения соответствующей ей однородной системы дает общее решение неоднородной системы:

,

где - частное решение неоднородной системы.