гос по ТЭС (последний)

1. Сообщения передаются 5-элементным кодом с равновероятными элементами по гауссовскому каналу связи со скоростью V=1000 Бод сигналами фазовой модуляции при отношении сигнал/шум h² = 5.

Рассчитать вероятность неправильного приема кодовой комбинации.

Для повышения помехоустойчивости используется корректирующий код (n,k) = (9,5), исправляющий однократные ошибки t_ош = 1. Рассчитать вероятность ошибочного декодирования принимаемых комбинаций при исправлении ошибок.

Решение:

Приём сигналов фазовой модуляции возможен только с помощью синхронного (когерентного) детектора, различающего фазы принимаемых сигналов.

При этом средняя вероятность ошибки приема одиночного импульса равна:

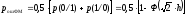
где h² – отношение сигнал/шум.

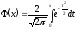- табулированный интеграл вероятностей (функция Крампа)

Тогда,

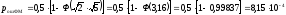
Для 5-элементного двоичного кода вероятность ошибки:

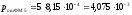
Вероятность неправильного приема кодовой комбинации при применении корректирующего кода, определяется как:

где р_ош – вероятность неправильного приема единичного элемента;

n– длина кодовой комбинации;

t – кратность исправляемых ошибок;

.

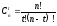Вероятность неправильного приема для корректирующего кода (n,k)=(9,5), исправляющего однократные ошибки t=1:

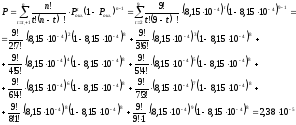
2. Определить амплитуды сигналов на входе идеального приемника Котельникова при дискретной фазовой модуляции (ДФМ) для следующих условий: априорные вероятности передачи сигналов равны P(S₁) = P(S₂) = 0,5, скорость передачи V=2000Бод; спектральная плотность мощности флуктуационной помехи на входе приемника Nо = 0,2∙10^-3 В²/Гц; средняя вероятность ошибки p_ош = 0,001.

Средняя вероятность ошибки для ДФМ: P_ош=0.5*(1-Ф(z)),

отсюда: Ф(z)=1- 2P_ош=1-2*0,001 = 0,998

по таблице значений функции Крампа находим для Ф(z)=0,998:

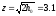
Учитывая, что для дискретной фазовой модуляции:

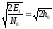, тогда:

;

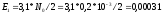
Поскольку по определению среднеквадратичное (действующее) значение напряжения: , а для синусоидального напряжения: получаем:

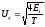
Амплитудa сигналов на входе идеального приемника Котельникова составит: ±Um/2=2,23/2=±1,11В

5. Непрерывный гауссовский канал связи используется для передачи двоичных равновероятных сообщений со скоростью 1000 Бод. Полоса пропускания канала связи 4кГц, отношение сигнал/шум Р_с/N₀=310³. Вычислить коэффициент использования пропускной способности канала связи.

Дано:

R=1000 Бод

F=4кГц

Р_с/N₀=310³

Найти:

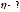
Решение:

Коэффициент использования пропускной способности канала связи (информационная эффективность) характеризует реальную скорость передачи информации R по отношению к пропускной способности С канала связи:

.

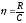Пропускную способность для гауссовского непрерывного канала связи с полосой частот ∆F можно найти как:

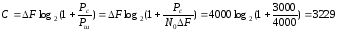
Следовательно, коэффициент пропускной способности канала связи:

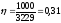
Информационная эффективность η всегда меньше единицы; чем ближе η к единице, тем совершеннее система.

6. Определить энтропию, избыточность и производительность двоичного источника дискретных сообщений, у которого априорная вероятность передачи символа x₁ равна 0,3, а скорость передачи 9600 Бод.

Дано:

p(x₁) = 0,3

R(x,y)=9600 Бод

Найти:

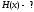
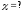
Решение:

Априорная вероятность передачи символа :

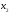Энтропия источника сообщений в общем случае определяется по формуле:

,

где 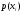- вероятность выдачи источником символов 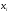(априорная вероятность);

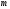- количество символов.

Энтропия двоичного источника дискретных сообщений:

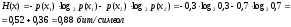
Количественно избыточность оценивается коэффициентом избыточности:

,

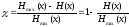где 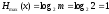- максимальная энтропия источника с алфавитом из m сообщений.

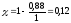
Производительность источника сообщений:

,

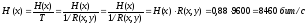где 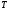- интервал времени для передачи элементарного сообщения;

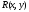- скорость передачи.

Ответ: , , .

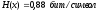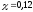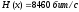8. Сообщение передается последовательностью амплитудно-модулированных импульсов с заданным шагом квантования ∆u. На сообщение накладываются шумы с нормальным законом распределения вероятности и дисперсией σ². Определить величину минимально допустимого шага квантования, при котором вероятность ошибки из-за шумов не превысит значения 0,05 (как известно, ошибка при квантовании возникает при условии, что мгновенное значение шума превышает половину шага квантования).

Если для дискретной амплитудной модуляции (ДАМ) средняя вероятность ошибки меньше 0,05 то:

,

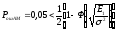где σ² –дисперсия.

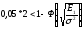
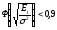
По таблице значений функции Крампа Ф(х) находим: 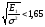, тогда .

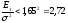Отсюда: Е₁<2.72σ²

Если среднее значение шума не должно превышать половину шага квантования, то Е₁ должно быть ≤∆u/2.

Следовательно: шаг квантования ∆u должен быть:

∆u=2* 2.72σ² =5,44σ²

9. На электронное реле воздействует случайное напряжение с релеевской плотностью распределения вероятностей и дисперсией σ² = 1 В². Определить вероятность срабатывания реле при условии, что порог срабатывания реле равен 2В. Сущность задачи проиллюстрировать приведением графиков w(u), u_вх(t), y(t).

В данном случае происходит срабатывание реле от случайного напряжения, и при рэлеевском распределении вероятность появления напряжения 2В равна:

График распределения вероятности срабатывания:

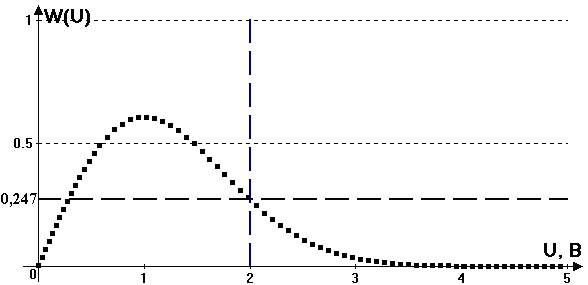
Графики входного напряжения и работы реле:

10. Вследствие замираний амплитуда радиосигнала на приеме случайна и распределена по закону Релея с дисперсией σ²_с = 2 В². Радиосигнал принимается на три разнесенные антенны, так что сигналы в каждой из антенн являются независимыми. Вычислить вероятность того, что сигнал на всех антеннах одновременно уменьшится ниже уровня 1,5 В.

Решение:

Для одной антенны вероятность того, что сигнал уменьшится ниже уровня 1,5 В составит:

Для трех антенн одновременно:

W₃(A)= 0,283*0,283*0,283 = 0,0227

11. Определите требуемую полосу пропускания канала передачи телевизионного изображения объемом 5∙10⁵ элементов при 25 кадрах в секунду и 8 равновероятными градациями яркости для отношения сигнал/шум P_с/P_ш = 20 и при условии, что изображение может принимать вид белого шума (т.е. наиболее хаотичный вид).

Решение:

Для передачи 8 градаций яркости необходимо 3 бита ( 8=2³ ), тогда для одного кадра нужно 3*5*10⁵=15*10⁵ бит, для передачи 25 кадров - 25*15*10⁵=37,5*10⁶

Ответ: требуемая полоса пропускания канала передачи: не менее 37,5 МГц.

12. Непрерывное сообщение с верхней границей спектра F_в = 3 кГц преобразуется методом ИКМ в двоичный сигнал с количеством уровней квантования 256. Определить скорость передачи двоичных символов в канале связи.

Рещение:

Для передачи 256 уровней квантования необходимо 8 символов:

2⁸=256.

При частоте спектра F_в = 3кГц согласно теореме Котельникова частота дискретизации должна составлять:

3*2=6 кГц.

Тогда скорость передачи двоичных символов в канале связи составит:

6*8=48 кбит/с.

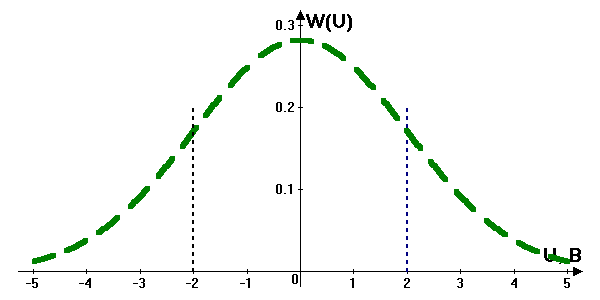
13. Гауссовский случайный шум с нулевым математическим ожиданием и дисперсией σ² поступает на детектор огибающей. Определить, с какой вероятностью сигнал на выходе детектора превышает значение 2σ. Сущность задачи проиллюстрировать приведением выражений и графиков w(u_вх), w(u_вых).

Решение:

Вероятность того, что мгновенное значение шума с нулевым средним уровнем m=0 и дисперсией σ² превысит уровень x₀ =2σ для гауссовского случайного процесса:

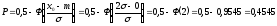
где Ф(2) находим по таблице значений функции Крампа.

Выражение для w(u_вх) для гауссовского случайного процесса в данном случае:

15. В системе связи передаются дискретные сообщения с помощью частотной модуляции ортогональными сигналами вида s₁(t) = a cosω₁t и s₂(t) = a cosω₂t. Необходимо скорость модуляции увеличить в 2 раза. Какие параметры сигналов, и каким образом нужно изменить, чтобы вероятность ошибки осталась прежней. Прием оптимальный некогерентный.

Средняя вероятность ошибки приема двух ортогональных частотно-манипулированных сигналов при оптимальном некогерентном приеме: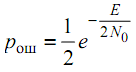

где E/N₀ – отношение энергии элемента сигнала к спектральной плотности мощности шума.

Принимаем спектральную плотность мощности шума независимой от частоты («белый шум»).

Следовательно, для того, чтобы вероятность ошибки на символ осталась прежней, энергия сигнала для одного элемента не должна изменяться.

Энергия сигнала: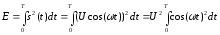

Поскольку при увеличении скорости модуляции в 2 раза период уменьшается в 2 раза, то при использовании прежних частот должно сохраняться соотношение Е₁=Е₂:

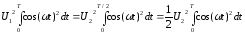
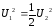
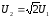
Ответ: при увеличении скорости модуляции в 2 раза необходимо увеличить амплитуду сигнала в 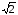раз.

17. В гауссовском канале связи с отношением сигнал/шум h² = 10 передаются с равной вероятностью двоичные сообщения с использованием амплитудной модуляции: скорость передачи 1000 Бод, полоса пропускания канала связи 6 кГц. Определить вероятность ошибки. Предложить меры по повышению помехоустойчивости и оценить ожидаемый при этом выигрыш.

Решение:

Средняя вероятность ошибки для амплитудной модуляции при некогерентном приеме:

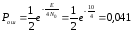
где E/N₀ =10 – отношение энергии элемента сигнала к спектральной плотности мощности шума.

В выражении для определения средней вероятности ошибки для повышения помехоустойчивости изменить можно только энергию сигнала: Е=P/F, то есть увеличить мощность передатчика или уменьшить несущую частоту.

Ширина спектра телеграфного сигнала обычно принимается равной 1,5V (Гц), где V – скорость телеграфирования в бодах, то есть необходима минимальная частота: 1000*1,5=3000 Гц=3кГц. В нашем случае применяется частота 6 кГц, то есть ее можно уменьшить в 6/3=2раза. При этом энергия увеличится в 2 раза, соответственно, отношение сигнал/шум будет равно 10*2=20 и средняя вероятность ошибки составит:

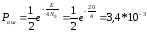
Увеличив мощность сигнала в 2 раза, получим такое же отношение сигнал/шум: 10*2=20 и аналогичную вероятность ошибки.

При необходимости дальнейшего повышения помехоустойчивости можно только повышать мощность сигнала.

19. Определить, какую мощность должен иметь сигнал с гауссовским законом распределения мгновенных значений для обеспечения пропускной способности 5000 бит/с в непрерывном канале связи с параметрами: полоса пропускания канала связи f_эфф = 1200 Гц, спектральная плотность мощности шума N_о = 10 мкВт/Гц.

Решение:

Пропускная способность гауссовского канала определяется по формуле:

,

где 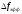- полоса пропускания непрерывного канала,

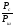- отношение мощности сигнала к мощности помехи.

Выразим мощность шума в канале через его спектральную плотность N₀:

.

Пропускная способность тогда будет:

.

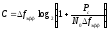Выразим мощность сигнала:

.

Ответ: сигнал должен иметь мощность 0,203 Вт.

20. Кодовая комбинация, передаваемая по дискретному каналу связи, состоит из пяти знаков, каждый из которых может быть либо «0», либо «1». Найти вероятность того, что в комбинации будет три нуля.

Решение:

Вероятность того, что в комбинации будет ровно три нуля (событие А) определим по формуле:

,

где 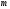- число комбинаций, в которых три нуля;

- количество всех возможных кодовых комбинаций.

Количество всех возможных кодовых комбинаций:

.

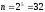Количество комбинаций, в которых три нуля:

.

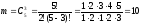Искомая вероятность будет:

.

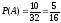Вероятность того, что в комбинации будет три или больше нулей (событие В):

.

Ответ: вероятность того, что в кодовой комбинации будет ровно три нуля – 5/16, три или больше нулей – 0,5.

21. Телеграфное сообщение состоит из сигналов «0» и «1». Статистические свойства помехи таковы, что искажаются в среднем 2/5 сигналов «нуль» и 1/3 сигналов «единица». Известно, что среди передаваемых сигналов «0» и «1» встречаются в соотношении 5:3. Определить вероятность того, что принят передаваемый сигнал, если:

а) принят сигнал «0»;

б) принят сигнал «1».

Решение:

Пусть событие А – принят сигнал «0», а событие В – принят сигнал «1».

Можно сделать две гипотезы: H₁ – передан сигнал «0», H₂ – передан сигнал «1».

По условию:

.

Кроме того,

.

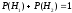Поэтому,

, .

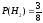По условию, вероятность того, что при передаче исказился сигнал «0» (передан сигнал «0», принят сигнал «1»):

.

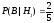Вероятность того, что при передаче исказился сигнал «1» (передан сигнал «1», принят сигнал «0»):

.

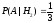Вероятности того, что сигналы не исказились:

.

.

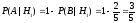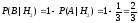Вероятности событий А и В определяем, используя формулу полной вероятности.

Вероятность того, что принят сигнал «0»:

.

Вероятность того, что принят сигнал «1»:

.

Вероятности того, что принят передаваемый сигнал, определяем, используя формулу Байеса.

Вероятность того, что принят передаваемый сигнал, если принят сигнал «0»:

.

Вероятность того, что принят передаваемый сигнал, если принят сигнал «1»:

.

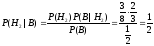Ответ: а) 3/4; б) 1/2.

22. Посланный радиолокатором сигнал, отражаясь от цели принимается из-за наличия помех с вероятностью 0,85. Какова вероятность того, что при пятикратной передаче сигнал будет принят 4 раза? Не менее 4 раз? Какое число принятых сигналов будет наивероятнейшим?

Решение:

В задаче рассматриваются независимые условия (испытания).

По условию, вероятность того, что сигнал принят: .

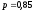Вероятность того, что сигнал не принят: .

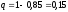Вероятность того, что событие наступит ровно в m испытаниях из n определим по формуле Бернулли:

Вероятность того, что при пятикратной передаче (n=5) сигнал будет принят 4 раза (m=4):

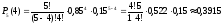
Вероятность того, что при пятикратной передаче сигнал будет принят не менее 4-х раз (то есть или четыре, или пять раз):

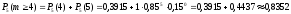
Наивероятнейшее число наступления события m определяется по формуле:

.

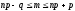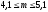
Значит, наивероятнейшим числом принятых вызовов будет 5.

Ответ: 0,3915; 0,8352; 5.

23. Известно, что 70% всех сообщений передано по кабельной линии связи (КЛС), а 30% по радиорелейной линии связи (РРЛ). Вследствие воздействия помех принимаются без искажений 90% всех сообщений по КЛС; по РРЛ – 60%. Определить вероятность того, что:

а) что первые два наугад выбранные сообщения переданы по КЛС; по РРЛ;

б) первое наугад выбранное сообщение окажется неискаженным и при этом переданным по КЛС; по РРЛ.

Решение:

а)

Вероятность того, что два выбранных сообщения переданы по КЛС определим по формуле:

,

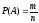где 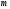- число благоприятных исходов;

- число всех возможных исходов.

Количество всех возможных исходов:

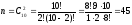
Количество благоприятных исходов:

.

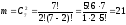Искомая вероятность будет:

.

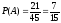Аналогично, определяем вероятность того, что два выбранных сообщения переданы по РРЛ.

Количество благоприятных исходов:

.

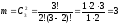Искомая вероятность будет:

.

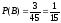б) Пусть событие А – принято неискаженное сообщение, а событие В – принятое сообщение искажено.

Можно сделать две гипотезы: H₁ – сообщение передано по КЛС; H₂ – сообщение передано по РРЛ.

Вероятности того, что сообщение передано по КЛС или РРЛ:

,

.

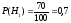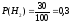По условию, вероятность того, что переданный по КЛС сигнал принят без искажений:

.

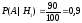Вероятность того, что переданный по РРЛ сигнал принят без искажений:

.

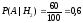Вероятности событий А и В определяем, используя формулу полной вероятности.

Вероятность того, что сигнал не исказился

.

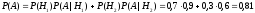Вероятность того, что принятый неискаженный сигнал, передавался по КЛС определяем, используя формулу Байеса:

.

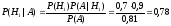Вероятность того, что принятый неискаженный сигнал, передавался по РРЛ:

.

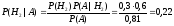Ответ: а) 7/15; 1/15; б) 0,78; 0,22.

24. По каналу связи, подверженному воздействию помех, передается одна из двух команд управления в виде кодовых комбинаций 11111 или 00000, причем априорные вероятности передачи этих команд соответственно равны 0,6 и 0,4. Из-за наличия помех вероятность правильного приема каждого из символов (1 или 0) уменьшается до 0,06. Предполагается, что символы кодовых комбинаций искажаются независимо друг от друга. На выходе приемного устройства зарегистрирована комбинация 10110. Определить, какая команда была передана (с какой вероятностью)?

Решение:

Вероятность получения r ошибок при передаче n символов подчиняется биномиальному закону:

,

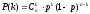где n – число символов;

n – количество ошибок;

p – вероятность ошибки приема одного символа.

Принимаемая комбинация имеет 5 символов, следовательно, если передавалась комбинация 00000, а принято 11010, то искажены 3 символа.

При этом вероятность такого искажения составит:

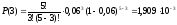
Если априорная вероятность передачи команды 00000 равна 0,4, то общая вероятность такой ситуации составит:

P₀₀₀₀₀=0,4*1,909*10^-3=0,76*10^-3

Аналогично, если передавалась комбинация 11111, а принято 11010, то искажены 2 символа, при этом вероятность такого искажения составит:

Если априорная вероятность передачи команды 11111 равна 0,6, то общая вероятность такой ситуации составит:

P₁₁₁₁₁=06*0,0299=17,9*10^-3

Тогда: P₁₁₁₁₁=17,9*10^-3 > P₀₀₀₀₀=0,76*10^-3

Ответ: наиболее вероятно, была передана команда 11111.

25. Производящий многочлен циклического кода (8,5) имеет вид g(x) = x³ + x + 1. Найти проверочные элементы кода, соответствующие передаваемой последовательности информационных элементов кода вида 10011, записать полученную комбинацию циклического кода. Проиллюстрировать также случай обнаружения однократной ошибки в принятой комбинации.

Решение:

Для нахождения проверочных элементов циклическрго кода дописываем справа к информационным символам три «0», преобразуем комбинацию в вид полинома и делим ее на на порождающий полином:

10011000=1*x⁷+0*x⁶+0*x⁵+1*x⁴+1*x³+0*x²+0*x+0*1=x⁷+x⁴+х³

x⁷+x⁴+х³ |x³+x+1

х⁷+х⁵+х⁴ х⁴+ х²

х⁵+х³

х⁵+х³+х²

х²

остаток равен: х²=100

Следовательно, в линию передаются:

информационные символы 10011 и проверочные 100.

Передаваемая комбинация циклическрго кода: «10011100».

Для обнаружения однократной ошибки допустим, что принята, например, комбинация 10111100.

Синдромный метод декодирования (СМД) предполагает в ДУ принятую кодовую комбинацию поделить на порождающий полином. Если принятая комбинация является разрешённой, т. е. не искажена помехами в канале связи, то остаток от деления будет нулевым. Ненулевой остаток свидетельствует о наличии в принятой кодовой комбинации ошибок, остаток от деления и называется синдромом.

Преобразуем принятую комбинацию в вид полинома и делим ее на на порождающий полином:

10111100=1*x⁷+0*x⁶+1*x⁵+1*x⁴+1*x³+1*x²+0*x+0*1=x⁷+x⁵+x⁴+х³+x²

x⁷+x⁵+х⁴+x³+x² |x³+x+1

х⁷+х⁵+х⁴ х⁴+ 1

0

х³+х²

х³+х+1

х²+х+1