
- •Глава 1. Алгебра матриц и линейные алгебраические уравнения
- •Матрицы.
- •1.1. Свойства матриц.
- •1.1.1. Некоторые свойства квадратных матриц.
- •1.2. Блочные матрицы
- •Например, матрицу
- •1.3. Задачи
- •Домашнее задание.
- •1.4. Определители.
- •1.4.1. Основные свойства определителей.
- •1.4.2. Способы вычисления определителей.
- •1.5. Задачи
- •Домашнее задание.
- •1.6. Обратная матрица.
- •1.7. Задачи
- •Домашнее задание.
- •1.8. Ранг матрицы.
- •1.8.1. Вычисление ранга матрицы.
- •1.9. Задачи
- •Домашнее задание.
- •1.10. Системы линейных алгебраических уравнений (слау).
- •1.10.1. Системы уравнений с квадратной матрицей.
- •1.10.2. Однородные системы.
- •1.10.3. Системы уравнений общего вида.
- •1.10.4. Метод Гаусса (метод исключения).
- •1.11. Задачи
- •Домашнее задание.
1.1. Свойства матриц.
Из всех операций
отношения
![]() для
матриц определена только операция
сравнения.Две
матрицы считаются равными только тогда,
когда они имеют одинаковое число строк
и столбцов и соответствующие элементы
обеих матриц равны.
для
матриц определена только операция
сравнения.Две
матрицы считаются равными только тогда,
когда они имеют одинаковое число строк
и столбцов и соответствующие элементы
обеих матриц равны.
Определены также следующие линейные операции с матрицами:
1)
Умножение
матрицы на число.
Если
![]() – матрица
– матрица![]() и
и![]() - число, то матрица
- число, то матрица![]() (или
(или![]() )
имеет размерность
)
имеет размерность![]() и элементы
и элементы![]() ,
то есть каждый элемент исходной матрицы
умножается на число
,
то есть каждый элемент исходной матрицы
умножается на число![]() .
Матрица
.
Матрица![]() называется матрицей, противоположной
матрице А и обычно обозначается просто
как
называется матрицей, противоположной
матрице А и обычно обозначается просто
как![]() .
Ее нельзя называть отрицательной
матрицей, поскольку матрица знака не
имеет!
.
Ее нельзя называть отрицательной
матрицей, поскольку матрица знака не
имеет!
2)
Сложение
матриц.
Если две матрицы
![]() и
и![]() имеют одинаковую размерность
имеют одинаковую размерность![]() ,
то их суммой будет новая матрица
,
то их суммой будет новая матрица![]() той же размерности
той же размерности![]() и такая, что
и такая, что![]() .
При этом имеют место соотношения:
.
При этом имеют место соотношения:
![]() - переместительное
свойство,
- переместительное
свойство,
![]() - свойство
ассоциативности.
- свойство
ассоциативности.
Доказательство
этих свойств достаточно очевидно. Под
разностью двух матриц А и В понимается
сумма матрицы А и матрицы, противоположной
матрице В:
![]() ,
поэтому для разности матриц также
справедливы все указанные выше свойства.
,
поэтому для разности матриц также
справедливы все указанные выше свойства.
Считается, что размерность нулевой матрицы О всегда согласована с размерностью произвольной матрицы А – m x n так, чтобы имело место равенство
A + O = O + A = A.
3)
Умножение
двух матриц.
Если
![]() -
-![]() матрица, а
матрица, а
![]() –
–
![]() матрица, то произведением матрицы
матрица, то произведением матрицы![]() на матрицу
на матрицу
![]() называется новая матрица
называется новая матрица
![]() размерности
размерности![]() ,
построенная по следующему правилу
,
построенная по следующему правилу
![]() .
.
Из определения следует, что две матрицы можно умножить только тогда, когда число столбцов левой матрицы равно числу строк правой матрицы. Поэтому в общем случае в произведении нельзя переставлять матрицы местами. Заметим, что квадратные матрицы одинаковой размерности умножать друг на друга можно всегда.
Если несколько матриц можно умножать попарно, то имеет место свойство ассоциативности:
![]() .
.
Действительно,
пусть
![]() .
Тогда
.
Тогда
![]() ,
,
![]()
![]() .
.
Результат суммирования в правых частях не зависит от порядка суммирования, и таким образом, свойство ассоциативности доказано.
Если для двух
матриц выполняется равенство
![]() ,
то говорят, что матрицы
,
то говорят, что матрицы![]() и
и
![]() являются перестановочными
или
коммутативными.
Однако в
общем случае произведение двух матриц
некоммутативно, то есть
являются перестановочными
или
коммутативными.
Однако в
общем случае произведение двух матриц
некоммутативно, то есть
![]() .
.
1.1.1. Некоторые свойства квадратных матриц.
Квадратная матрица
![]() называетсясимметричной,
если
называетсясимметричной,
если
![]() ,
то есть если
,
то есть если![]() .
Для квадратной матрицы, которую всегда
можно умножать саму на себя, определено
понятиестепени
матрицы
.
Для квадратной матрицы, которую всегда
можно умножать саму на себя, определено
понятиестепени
матрицы
![]() как ее произведение самой на себяk
раз.
как ее произведение самой на себяk
раз.
В квадратной
матрице определено понятие главной и
побочной диагоналей. Главной
диагональю
называется совокупность элементов
матрицы, расположенных на воображаемой
линии, проведенной из верхнего левого
угла матрицы в правый нижний, а побочной
– их совокупность, расположенных на
аналогичной линии, проведенной из
верхнего правого угла в левый нижний.
Таким образом, элементами главной
диагонали является совокупность
![]() ,
а побочной -
,
а побочной -![]() .
.
Если все элементы матрицы А, расположенные ниже главной диагонали равны нулю, то такая матрица называется верхней треугольной матрицей.

Если же равны нулю все элементы, расположенные выше главной диагонали, то матрица А называется нижней треугольной

Единичной матрицей называется квадратная матрица, элементы главной диагонали которой равны единице, а все остальные – нули. Единичная матрица обычно обозначается буквой Е :
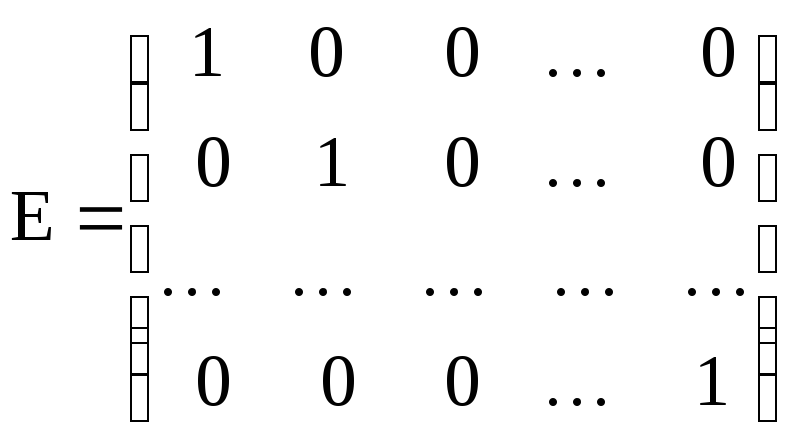 .
.
Считается, что
размерность единичной матрицы всегда
является согласованной с размерностью
любой (не
обязательно квадратной!) матрицы так,
чтобы имело место соотношение
![]() .
.
Квадратная матрица,
у которой отличны от нуля только элементы
ее главной диагонали, называется
диагональной
и обозначается как
![]() .
.
Приведем некоторые важные соотношения для матриц произвольной размерности (докажите их самостоятельно в качестве упражнения):
1)
![]() ;
2)
;
2)![]() ;
;
3)
![]() - симметричная матрица.
- симметричная матрица.
