
- •Глава 1. Алгебра матриц и линейные алгебраические уравнения
- •Матрицы.
- •1.1. Свойства матриц.
- •1.1.1. Некоторые свойства квадратных матриц.
- •1.2. Блочные матрицы
- •Например, матрицу
- •1.3. Задачи
- •Домашнее задание.
- •1.4. Определители.
- •1.4.1. Основные свойства определителей.
- •1.4.2. Способы вычисления определителей.
- •1.5. Задачи
- •Домашнее задание.
- •1.6. Обратная матрица.
- •1.7. Задачи
- •Домашнее задание.
- •1.8. Ранг матрицы.
- •1.8.1. Вычисление ранга матрицы.
- •1.9. Задачи
- •Домашнее задание.
- •1.10. Системы линейных алгебраических уравнений (слау).
- •1.10.1. Системы уравнений с квадратной матрицей.
- •1.10.2. Однородные системы.
- •1.10.3. Системы уравнений общего вида.
- •1.10.4. Метод Гаусса (метод исключения).
- •1.11. Задачи
- •Домашнее задание.
1.8.1. Вычисление ранга матрицы.
Для нахождения ранга матрицы в основном используются два метода - метод окаймляющих миноров и метод элементарных преобразований (метод Гаусса).
При использовании
метода
окаймляющих миноров
выделяют в матрице минор k-го
порядка
![]() ,
отличный от нуля и далее рассматривают
те минорыk+1
–го порядка, которые содержат в себе
(окаймляют) минор
,
отличный от нуля и далее рассматривают
те минорыk+1
–го порядка, которые содержат в себе
(окаймляют) минор
![]() .
Если все они равны нулю, то ранг матрицы
равенk,
в противном случае среди окаймляющих
миноров найдется ненулевой минор порядка
k+1
и вся процедура повторяется.
.
Если все они равны нулю, то ранг матрицы
равенk,
в противном случае среди окаймляющих
миноров найдется ненулевой минор порядка
k+1
и вся процедура повторяется.
Под элементарными преобразованиями понимаются следующие операции со строками (или столбцами) матрицы:
1) перестановка строк;
2) умножение любой строки на число, отличное от нуля;
3) сложение строк.
Нетрудно видеть, что эти элементарные преобразования не меняют ранга матрицы и метод Гаусса состоит в приведении исходной матрицы с помощью указанных элементарных преобразований к так называемому «ступенчатому» виду, в ходе которого получающиеся нулевые строки вычеркиваются.
Матрицу будем называть «ступенчатой», если она удовлетворяет следующим условиям:
1) первый элемент ее первой строки является ненулевым;
2) в каждой последующей ненулевой строке число нулевых элементов, предшествующих первому ненулевому, больше, чем у предыдущей строки.
После приведения матрицы к «ступенчатой» виду, ее ранг будет равен числу строк в матрице. Заметим, что структуры исходной и «ступенчатой» матриц различны, но их ранги одинаковы. Примеры «ступенчатых» матриц:
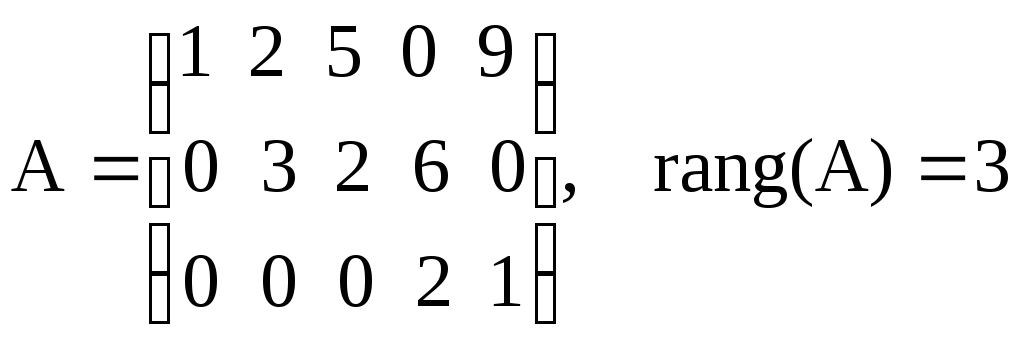 ;
;
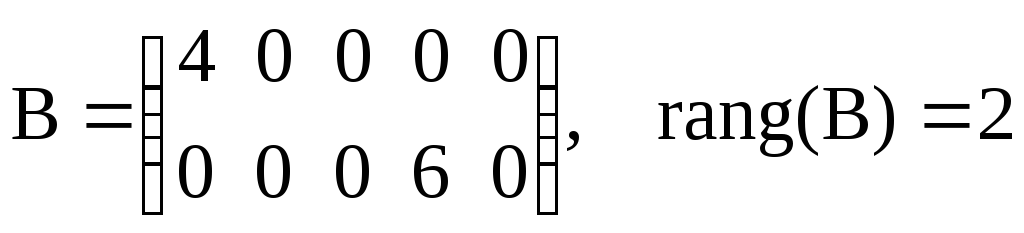 .
.
1.9. Задачи
Найти ранг матрицы методом окаймляющих миноров:
1.
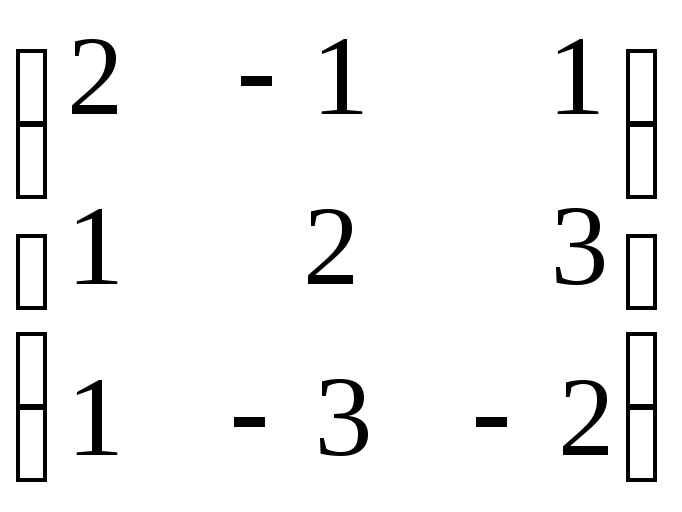 . 2.
. 2. .
.
Найти ранг матрицы методом Гаусса:
3.
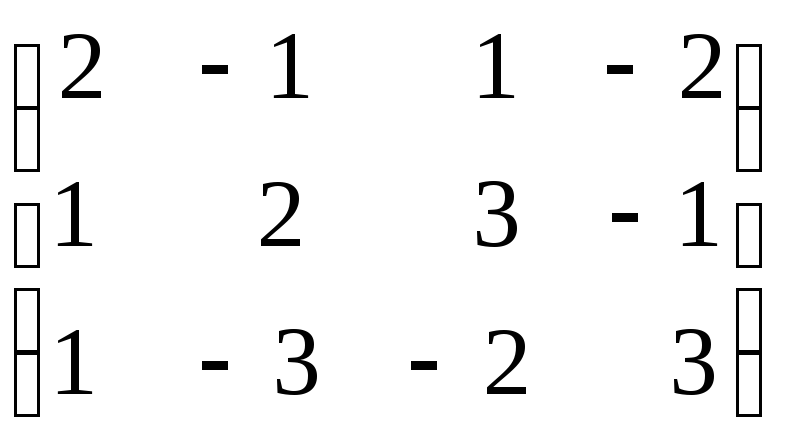 . 4.
. 4. .
.
5. Найти значения
![]() ,
при которых матрица
,
при которых матрица

имеет: а)
![]() ; б)
; б)![]() ; в)
; в)![]() .
.
Домашнее задание.
6. Найти ранг матрицы методом окаймляющих миноров:
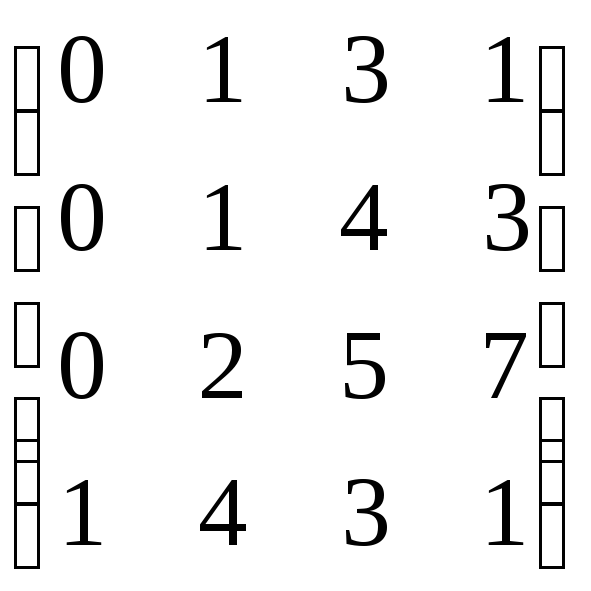 .
.
7. Найти значение
![]() ,
при котором ранги матрицА
и В
равны (использовать метод элементарных
преобразований):
,
при котором ранги матрицА
и В
равны (использовать метод элементарных
преобразований):
 ,
, 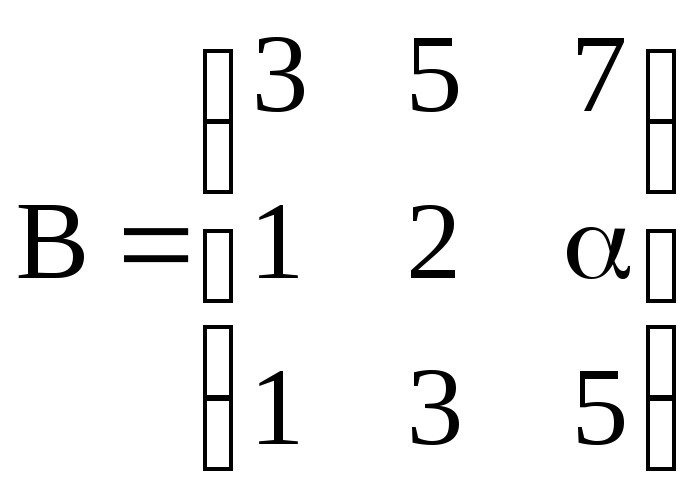 .
.
8. Найти ранг матрицы
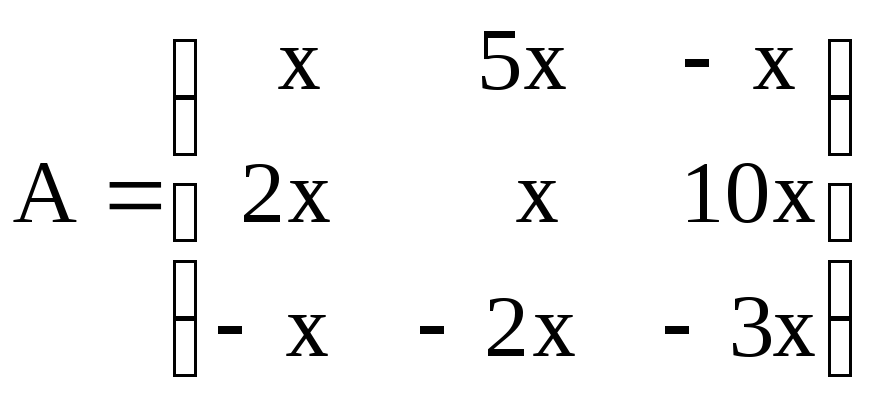 .
.
Ответы.
1. 2. 2. 3. 3. 3. 4. 2. 5. а) нет значений;
б)
![]() ;
в)
;
в)![]() .
6. 4. 7.
.
6. 4. 7.![]() .
8.
.
8.![]() ,
если
,
если![]() ;
;![]() ,
если
,
если![]() .
.
1.10. Системы линейных алгебраических уравнений (слау).
В общем случае система из m линейных алгебраических уравнений с n неизвестными имеет вид:
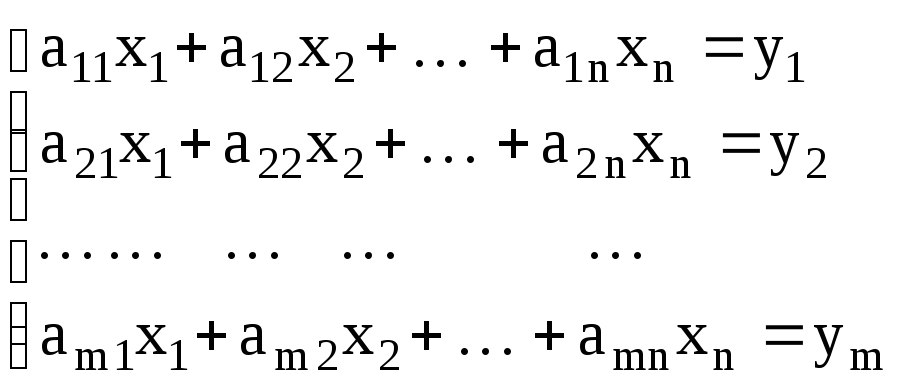 ,
(1.6)
,
(1.6)
при этом
![]() - неизвестные, подлежащие определению.
Известными величинами являются
коэффициенты системы
- неизвестные, подлежащие определению.
Известными величинами являются
коэффициенты системы![]() и свободные члены
и свободные члены![]() (правые части). В матрично-векторном
виде данная система уравнений записывается
в следующей компактной форме:
(правые части). В матрично-векторном
виде данная система уравнений записывается
в следующей компактной форме:
![]() ,
,
где
 ,
,
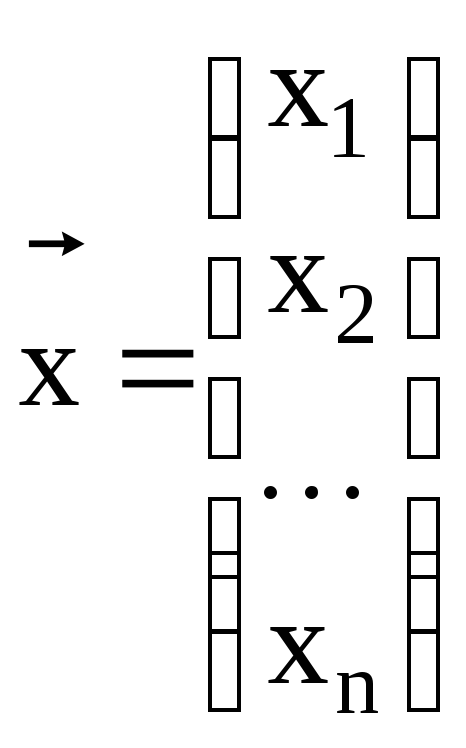 ,
,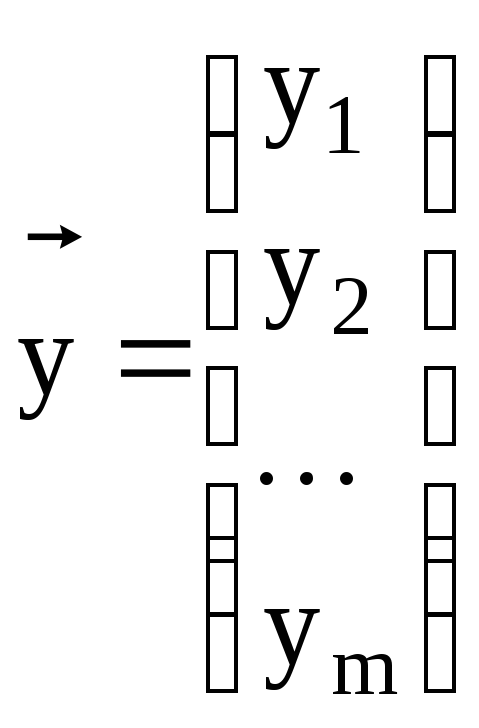 .
.
Если все члены
правых частей равны нулю (![]() ),
то система уравнений называетсяоднородной.
),
то система уравнений называетсяоднородной.
Решением системы
(1.6) называется такая совокупность чисел
![]() ,
которая при подстановке в (1.6) вместо
,
которая при подстановке в (1.6) вместо![]() обращает систему (1.6) в тождество. Не
всякая система вида (1.6) имеет решение.
Так, система
обращает систему (1.6) в тождество. Не
всякая система вида (1.6) имеет решение.
Так, система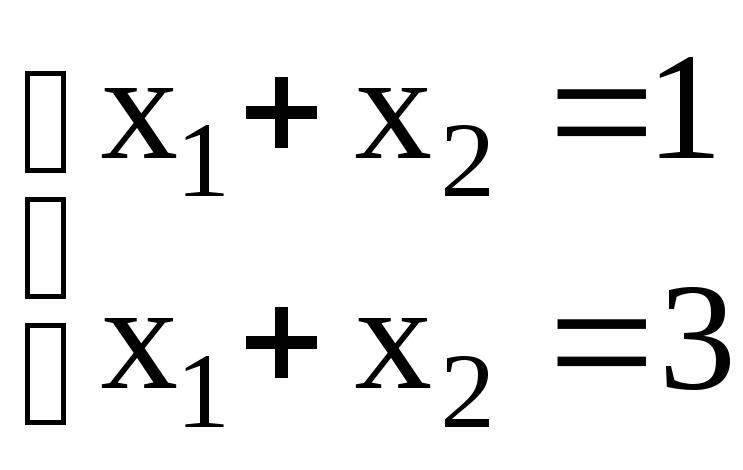 заведомо не имеет ни одного решения.
заведомо не имеет ни одного решения.
Определение. Система (1.6) называется совместной, если она имеет хотя бы одно решение и несовместной в противном случае.
Совместная система вида (1.6) называется определенной, если она имеет единственное решение и неопределенной, если имеет хотя бы два различных решения.
Условие совместности системы (1.6) можно установить с помощью теоремы Кронекера-Капелли.
Теорема (Кронекер-Капелли). Для того чтобы линейная система (1.6) являлась совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу ее основной матрицы.
Здесь под основной
матрицей системы (1.6) понимается матрица
А, а под расширенной – матрица
![]() ,
полученная из матрицы А путем добавления
к ней справа вектора – столбца свободных
членов системы (1.6):
,
полученная из матрицы А путем добавления
к ней справа вектора – столбца свободных
членов системы (1.6):
 .
.
Условия совместности
можно записать в виде:
![]() .
.
Пример.
1)
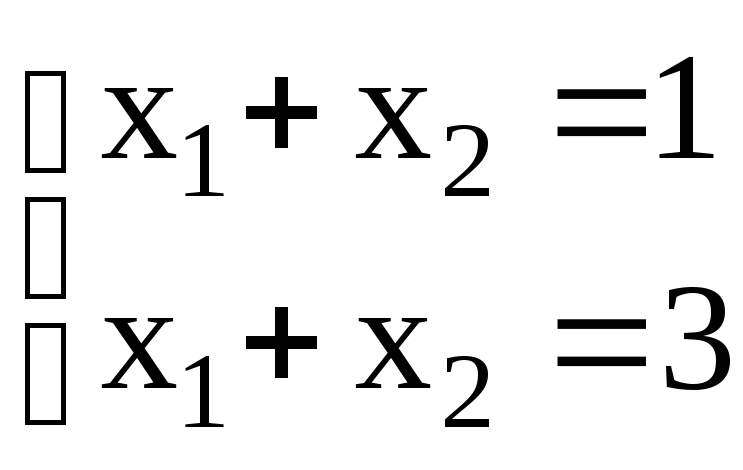 ,
,![]() ,
,![]() .
Система несовместна.
.
Система несовместна.
2)
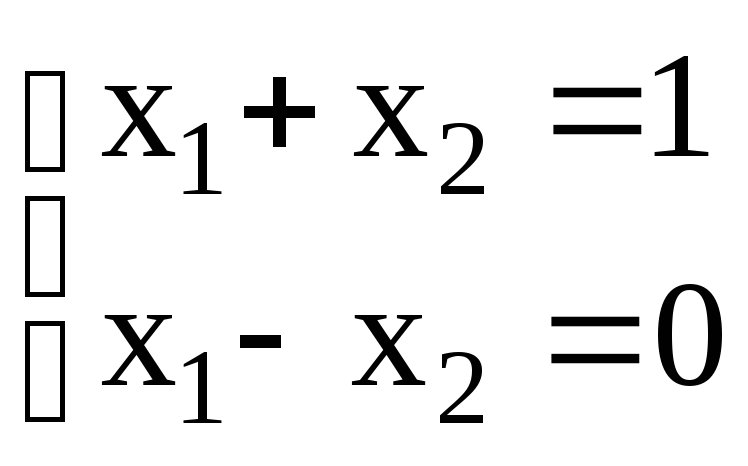 ,
,![]() ,
,![]() .
Система совместна.
.
Система совместна.
