
- •Глава 1. Алгебра матриц и линейные алгебраические уравнения
- •Матрицы.
- •1.1. Свойства матриц.
- •1.1.1. Некоторые свойства квадратных матриц.
- •1.2. Блочные матрицы
- •Например, матрицу
- •1.3. Задачи
- •Домашнее задание.
- •1.4. Определители.
- •1.4.1. Основные свойства определителей.
- •1.4.2. Способы вычисления определителей.
- •1.5. Задачи
- •Домашнее задание.
- •1.6. Обратная матрица.
- •1.7. Задачи
- •Домашнее задание.
- •1.8. Ранг матрицы.
- •1.8.1. Вычисление ранга матрицы.
- •1.9. Задачи
- •Домашнее задание.
- •1.10. Системы линейных алгебраических уравнений (слау).
- •1.10.1. Системы уравнений с квадратной матрицей.
- •1.10.2. Однородные системы.
- •1.10.3. Системы уравнений общего вида.
- •1.10.4. Метод Гаусса (метод исключения).
- •1.11. Задачи
- •Домашнее задание.
1.7. Задачи
1. Найти обратную матрицу для А методом присоединенной матрицы и проверить правильность ответа:
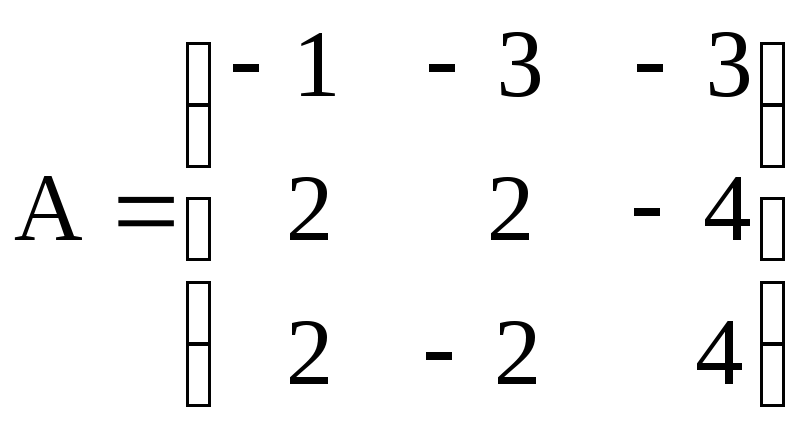 .
.
Найти обратную матрицу с помощью элементарных преобразований:
2.
![]() . 3.
. 3.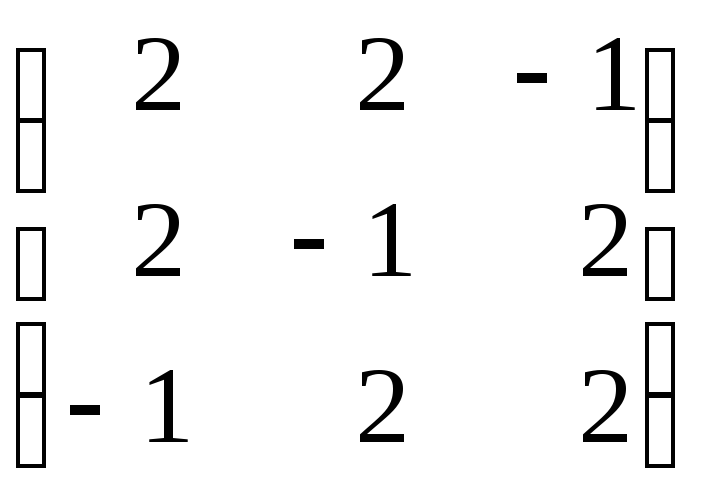 .
.
Решить матричное уравнение:
4.
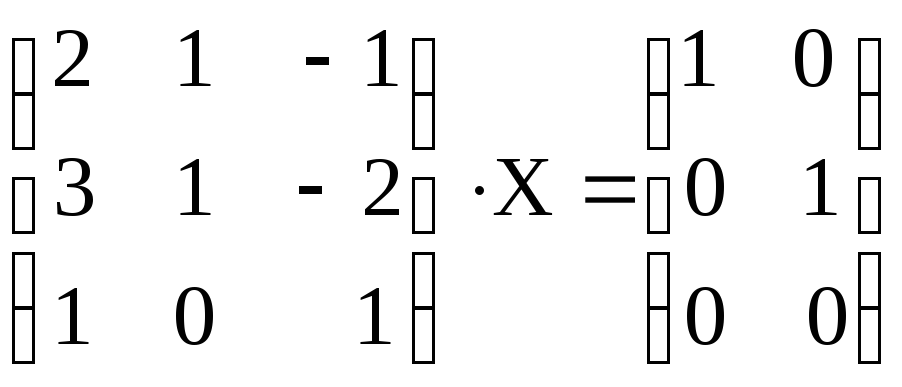 .5.
.5.
![]() .
.
Домашнее задание.
Найти обратную матрицу двумя способами (методом присоединенной матрицы; с помощью элементарных преобразований), сделать проверку:
6.
![]() . 7.
. 7. .
.
Решить матричное уравнение:
8.
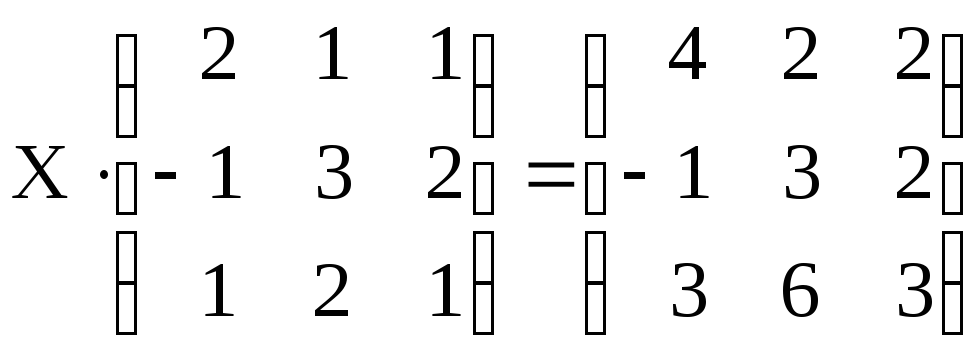 .
.
9.
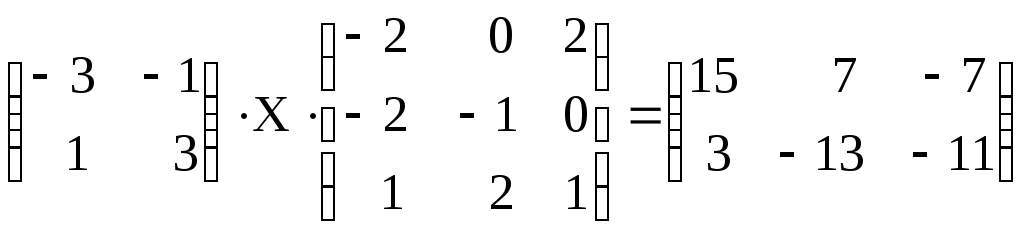 .
.
Ответы.
1.
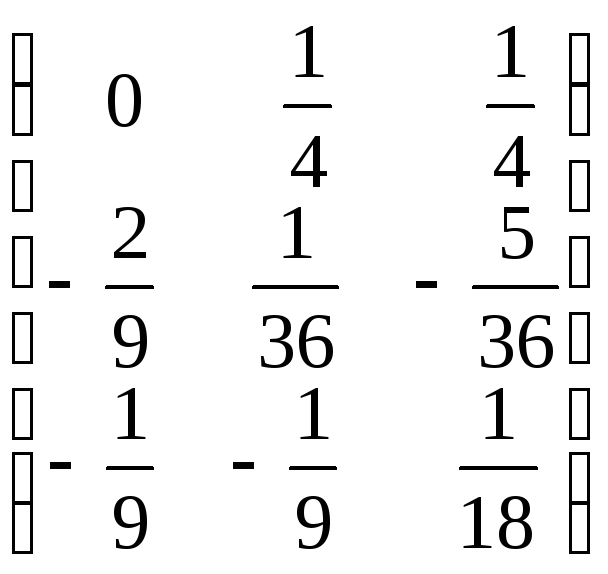 .
2.
.
2.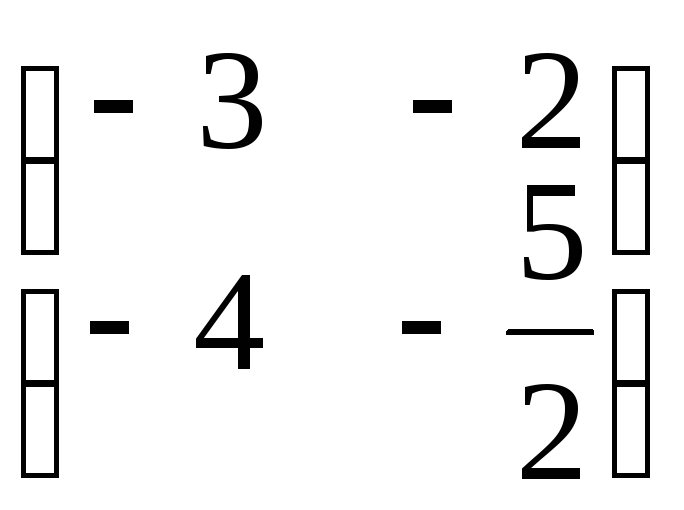 .
3.
.
3.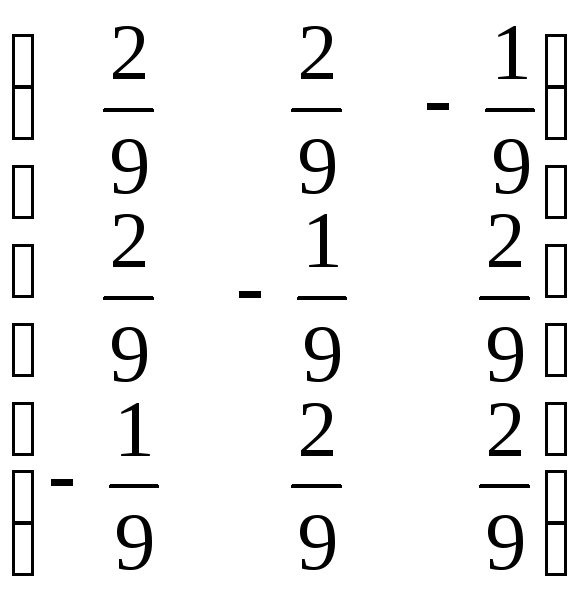 .
4.
.
4.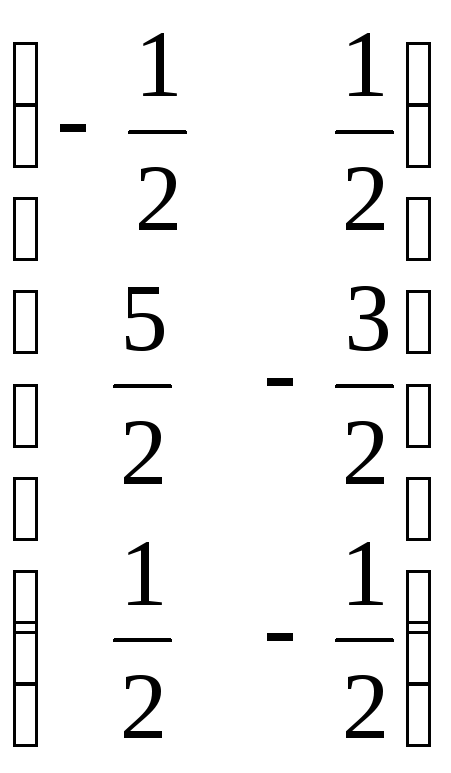 .
.
5.
![]() .
6.
.
6.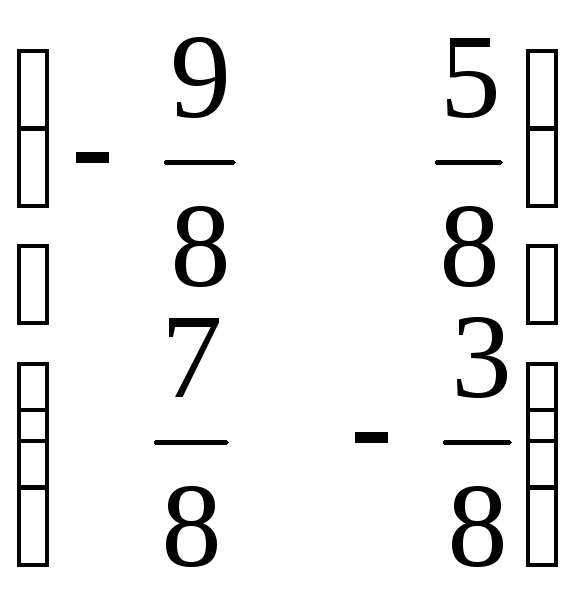 .
7.
.
7.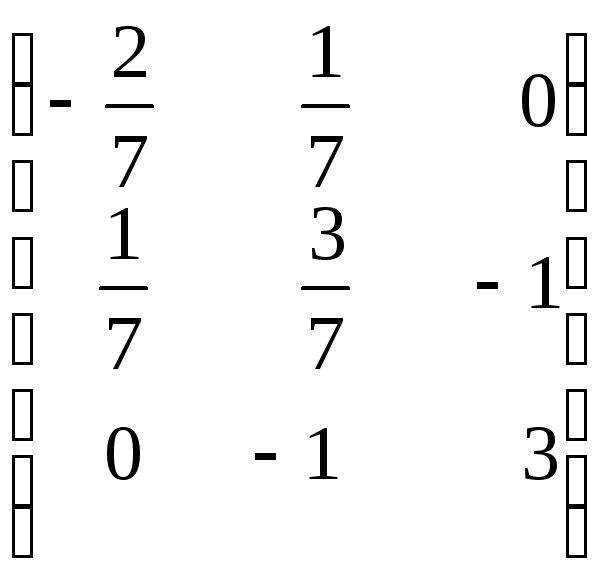 .
8.
.
8.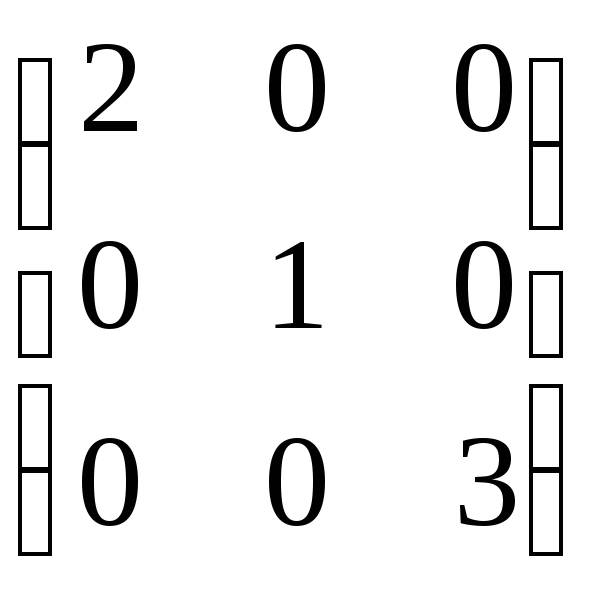 .
.
9.
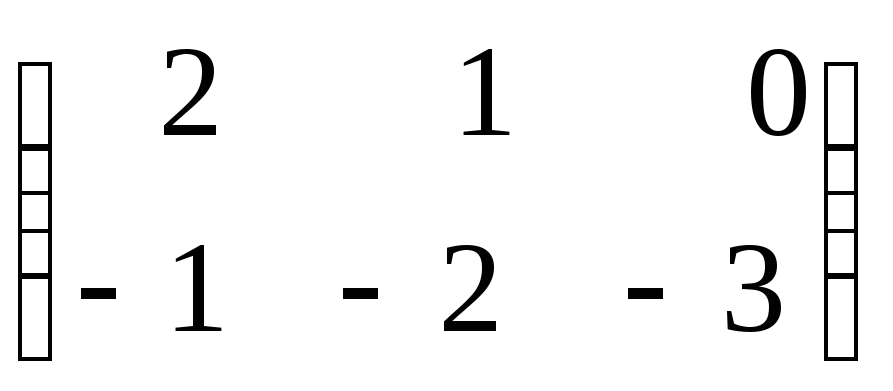 .
.
1.8. Ранг матрицы.
Рассмотрим
произвольную матрицу А – m
x
n.
Минором
второго
рода k-го
порядка матрицы А называется определитель
k-го
порядка с элементами, лежащими на
пересечении любых различных k
строк и k
столбцов (![]() ),
и обозначается как
),
и обозначается как![]() .
Число таких миноров равно числу сочетаний
.
Число таких миноров равно числу сочетаний![]() изN
по k,
где
изN
по k,
где
![]() .
.
Целое число r,
равное наибольшему порядку минора,
отличного от нуля, называется рангом
матрицы
А и обозначается как
![]() .
.
Минор r-го порядка, определяющий ранг матрицы, называется базисным минором, а строки и столбцы матрицы, на пересечении которых стоит базисный минор, называются базисными строками и базисными столбцами этой матрицы. Понятно, что базисных миноров может быть несколько.
Рассмотрим некоторые
свойства базисного минора. Прежде всего,
заметим, что перестановка строк и
столбцов не меняет ранга матрицы, то
есть
![]() ,
поскольку значение определителя при
этом не меняется.
,
поскольку значение определителя при
этом не меняется.
Для совокупности
из n
элементов любой природы
![]() введем понятиелинейной
комбинации
как суммы этих элементов, каждый из
которых предварительно умножен на
какое-то число
введем понятиелинейной
комбинации
как суммы этих элементов, каждый из
которых предварительно умножен на
какое-то число
![]() :
:
![]() .
.
Пусть
![]() ,
,
![]() ,
…,
,
…,![]() - вектор - строки матрицы А –m
x
n.
- вектор - строки матрицы А –m
x
n.
Определение.
Строки
![]() назовемлинейно
зависимыми,
если найдутся такие числа
назовемлинейно
зависимыми,
если найдутся такие числа
![]() не равные нулю одновременно, когда их
линейная комбинация равна нулю, то есть
справедливо равенство:
не равные нулю одновременно, когда их
линейная комбинация равна нулю, то есть
справедливо равенство:
![]() .
.
Если же это равенство возможно лишь в том случае, когда
![]() ,
то строки
,
то строки
![]() называютсялинейно
независимыми.
Из этих определений непосредственно
вытекают два важных следствия.
называютсялинейно
независимыми.
Из этих определений непосредственно
вытекают два важных следствия.
Следствие 1. Если любая часть совокупности элементов линейно зависима, то линейно зависима и вся совокупность.
Следствие 2. Если линейно независима вся совокупность элементов, то линейно независима и любая ее часть.
Нетрудно видеть,
что если строки являются линейно
зависимыми, то одна из них может быть
представлена в виде линейной комбинации
других. Пусть, например,
![]() .
Тогда
.
Тогда
![]() .
.
Теорема (о базисном миноре). Базисные строки (базисные столбцы) линейно независимы, при этом любая строка (любой столбец) матрицы А является линейной комбинацией базисных строк (базисных столбцов).
Доказательство. Все рассуждения проведем для строк. Если бы базисные строки были линейно зависимы, то одна из них была бы линейной комбинацией других базисных строк. Тогда, не меняя величины базисного минора, можно вычесть из этой строки указанную линейную комбинацию и получить строку, состоящую из одних нулей. А это означает, что базисный минор будет равен нулю, что противоречит определению базисного минора. Следовательно, базисные строки линейно независимы.
Докажем вторую
часть теоремы. Так как для базисного
минора важно лишь его отличие от нуля,
а не его знак, можно перестановкой строк
и столбцов матрицы А добиться того,
чтобы базисный минор располагался в
левом верхнем углу матрицы А. Итак, пусть
базисный минор располагается в первых
r
строках и в первых r
столбцах матрицы А. Пусть j
- любое натуральное число, принимающее
значение от единицы до n
(![]() )
иk
– любое число от r
до m
(
)
иk
– любое число от r
до m
(![]() ).
Убедимся, что равен нулю определительr+1
–го порядка
).
Убедимся, что равен нулю определительr+1
–го порядка
 .
.
Действительно,
если
![]() ,
то определитель равен нулю в силу того,
что он имеет два одинаковых столбца.
Если же
,
то определитель равен нулю в силу того,
что он имеет два одинаковых столбца.
Если же![]() ,
то он является минором матрицы А, который
имеет
,
то он является минором матрицы А, который
имеет![]() -й порядок и равен нулю по определению
базисного минора. Разложим этот
определитель по элементам последнего
столбца:
-й порядок и равен нулю по определению
базисного минора. Разложим этот
определитель по элементам последнего
столбца:
![]() .
.
Таким образом,
![]() (1.5)
(1.5)
для всех
![]() .
При этом
.
При этом![]() ,
так как
,
так как![]() (
(![]() - базисный минор). Разделим равенство
(1.5) на
- базисный минор). Разделим равенство
(1.5) на![]() .
Получим
.
Получим
![]() .
.
Или
![]() ,
,
то есть k-тая строка является линейной комбинацией базисных строк. Теорема доказана.
Теорема. Для
того, чтобы определитель n-го
порядка
![]() был равен нулю, необходимо и достаточно,
чтобы его строки (или столбцы) были
линейно зависимыми.
был равен нулю, необходимо и достаточно,
чтобы его строки (или столбцы) были
линейно зависимыми.
Доказательство.
1) Необходимость.
Если
![]() ,
то базисный минор его матрицы имеет
порядокr
< n.
Но тогда хотя бы одна его строка является
линейной комбинацией базисных строк
этого минора, то есть строки линейно
зависимы.
,
то базисный минор его матрицы имеет
порядокr
< n.
Но тогда хотя бы одна его строка является
линейной комбинацией базисных строк
этого минора, то есть строки линейно
зависимы.
2) Достаточность.
Если строки определителя
![]() линейно зависимы, то одна из них является
линейной комбинацией других. Вычитая
из нее эту линейную комбинацию, что не
меняет значения определителя, получим
строку, целиком состоящую из нулей. А
это означает, что
линейно зависимы, то одна из них является
линейной комбинацией других. Вычитая
из нее эту линейную комбинацию, что не
меняет значения определителя, получим
строку, целиком состоящую из нулей. А
это означает, что![]() .
Теорема доказана.
.
Теорема доказана.
