1.4.1. Основные свойства определителей.

1. Если поменять местами строки и столбцы определителя, то значение определителя не изменится: 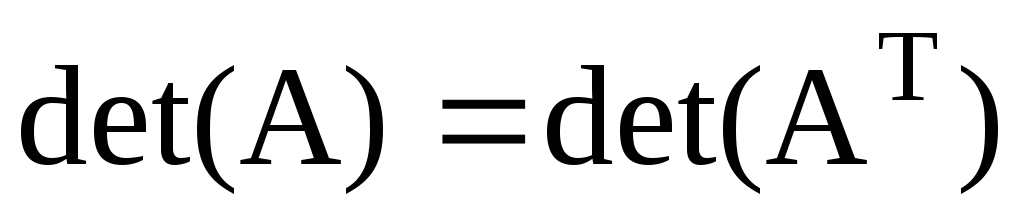. Это свойство следует из эквивалентности разложения по строкам и столбцам.

2. При перестановке местами двух строк или столбцов определитель меняет знак на противоположный (доказано ранее).

3. Умножение всех элементов некоторой строки (или столбца) определителя на число равносильно умножению определителя на это число. Доказательство следует из разложения по данной строке.

4. Если элементы двух строк (или столбцов) равны или пропорциональны, то определитель равен нулю. Доказательство следует из разложения определителя по своей и «чужой» строке.

5. Если все элементы некоторой строки или столбца равны нулю, то определитель равен нулю. Доказательство следует из разложения по этой строке.

6. Если к элементам некоторой строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель , то значение определителя не изменится.

7. Для двух квадратных матриц А и В порядка n справедливо соотношение: .

8. Если два определителя 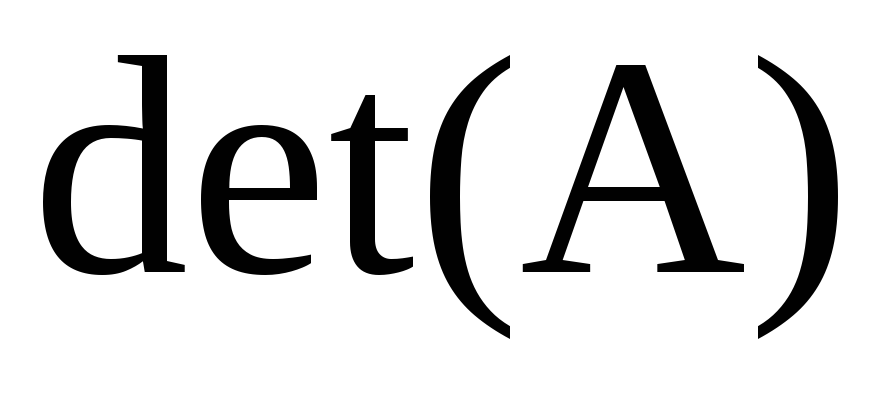иодного порядка отличаются только одним столбцом (или строкой), то их сумма есть определитель того же порядка и с теми же элементами, кроме указанного столбца (или строки), который есть сумма элементов соответствующих столбцов (строк) первых двух определителей, то есть

.

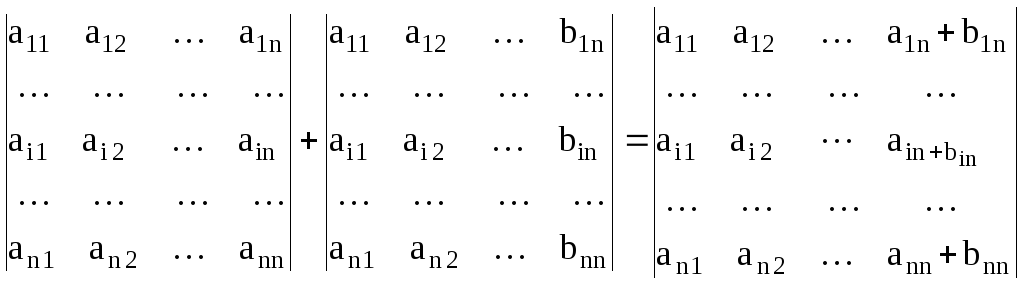Действительно, вычисляя определители в левой и правой частях приведенного равенства путем разложения по последнему столбцу и учитывая, что алгебраические дополнения у них одинаковы, получим

Докажем свойство 6.

Пусть .

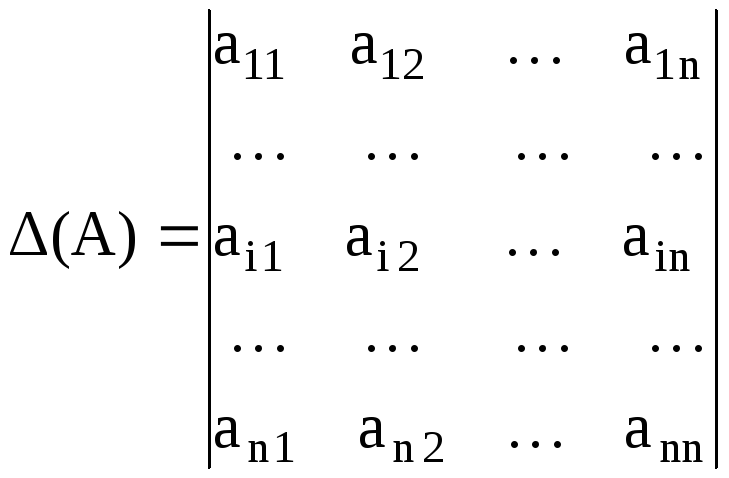Составим новый определитель, прибавив к элементам i -той строки элементы первой, умноженные на некоторое число :

.

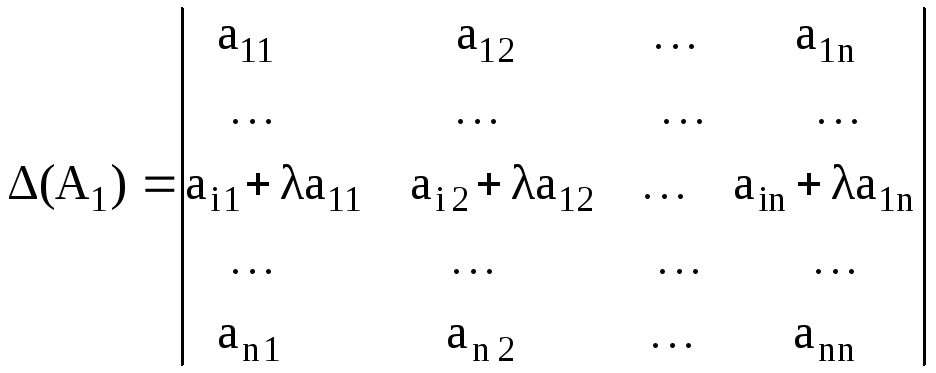Разложим оба определителя по i-той строке:

.

Алгебраические дополнения у них одинаковы. При этом

,

поскольку как результат разложения по «чужой» строке. Свойство доказано.

Свойство 7, которое часто будем использовать в дальнейшем, докажем на примере умножения двух определителей второго порядка. Пусть даны две матрицы А и В размерности 2

.

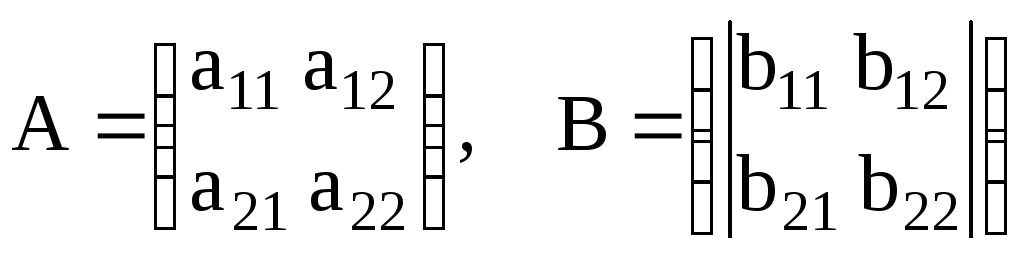Тогда их произведение есть матрица

.

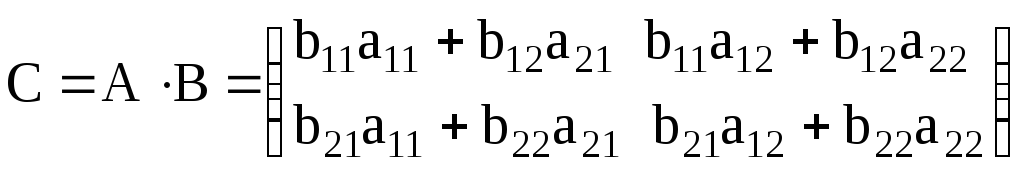Вычислим определитель этой матрицы, используя приведенные выше свойства определителей

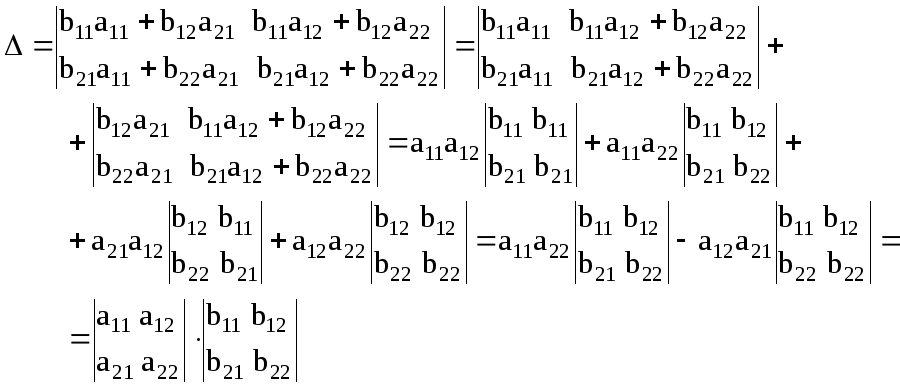
Свойство доказано.

1.4.2. Способы вычисления определителей.

Вычисление определителей высоких порядков по формулам (1.1) или (1.2) требует выполнения большого объема вычислительной работы, связанного с вычислением алгебраических дополнений. Значительно сократить этот объем можно за счет предварительного преобразования строк или столбцов определителя, используя свойство 6. Назовем операцию сложения какой-либо строки (или столбца) определителя с любой другой строкой (столбцом), предварительно умноженной на произвольное число эквивалентным преобразованием этой строки (столбца), поскольку при этом значение определителя не изменяется. Тогда с помощью таких эквивалентных преобразований всегда можно добиться того, чтобы какая-то строка (или столбец) содержала как можно больше нулевых элементов. Тогда при разложении по этой строке (или по столбцу) алгебраические дополнения нужно вычислять только для ненулевых элементов данной строки (столбца). Этот способ называют иногда методом нулей, вкладывая в него изложенный выше смысл.

Более общий подход заключается в приведении определителя с помощью эквивалентных преобразований строк (или столбцов) к треугольному виду. Сложим вторую строку с первой (которую назовем базовой), предварительно умноженной на число . Тогда первый элемент преобразованной второй строки будет нулевым. Аналогичным образом, умножая поочередно первую строку напреобразуем все остальные строки определителя, в результате чего получим определитель, равный исходному, у которого все элементы первого столбца, кроме первого, являются нулевыми. Далее, выберем в полученном определителе в качестве базовой вторую строку и подобным же образом преобразуем все строки ниже базовой. Продолжая этот процесс, получим в итоге определитель с верхней треугольной матрицей

,

значение которого вычисляется последовательным применением разложения по столбцу (1.2) и, как легко показать, равно произведению элементов, стоящих на главной диагонали:

.

Этот метод легко алгоритмизуется и может быть реализован на ЭВМ при вычислении определителей любого порядка. Возможности деления на нуль при вычислении множителя всегда можно избежать путем соответствующей перестановки строк или столбцов, учитывая, что при таких перестановках определитель меняет свой знак на противоположный.