
Вычеты
.pdf
Лекция 9. ВЫЧЕТЫ
1.Определение вычета и основная теорема о вычетах.
2.Вычисление вычетов.
3.Логарифмический вычет.
4.Вычет функции относительно бесконечно удаленной точки
1. Определение вычета и основная теорема о вычетах.
Пусть f (z) – функция, аналитическая в каждой точке облас-
ти E , за исключением конечного числа изолированных особых точек, и Γ – кусочно-гладкий замкнутый контур, целиком лежащий в области E и не проходящий через особые точки функ-
ции f (z). И пусть точка z0 является изолированной особой точ- |
|||||||||||||||||
кой функции f (z), причем в кольце 0 < |
|
z − z0 |
|
< R эта функция |
|||||||||||||
|
|
||||||||||||||||
является |
|
аналитической. |
Разложение |
|
|
функции |
|
f (z) в кольце |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|||
0 < |
|
z − z0 |
|
< R в ряд Лорана имеет вид |
f (z)= ∑cn (z − z0 )n , где |
||||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
f (ζ ) |
|
|
|
|
|
|
n=−∞ |
|||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
cn = |
|
Γ∫+ (ζ − z0 )n+1 |
dζ , n = 0,±1,±2,K. |
||||||||||
|
|
|
|
2π i |
|||||||||||||
Определение 1. Вычетом аналитической функции f (z) |
|||||||||||||||||
в изолированной особой точке |
z0 |
называется комплексное чис- |
|||||||||||||||
ло, равное значению интеграла |
1 |
|
∫ f (z)dz , взятому в положи- |
||||||||||||||
2π i |
|||||||||||||||||
|
|
|
|
|
|
|
|
Γ |
+ |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
тельном направлении по любому замкнутому кусочно-гладкому контуру Γ, лежащему в области аналитичности функции f (z) и
содержащему внутри себя |
единственную особую точку z0 |
||||
функции f (z). |
|
|
|
|
|
Обозначается: Res f (z0 ). |
|
|
|
|
|
Таким образом, |
|
|
1 |
|
|
Res f (z0 )= |
|
f (z)dz . |
|||
2π i |
|||||
z =z0 |
|
∫+ |
|||
|
|
|
|
Γ |
|
|
88 |
|
|
||
Если в выражении cn = |
1 |
∫+ (ζ −f (zζ ))n+1 dζ |
положить n = −1, |
|||||||||
2π i |
||||||||||||
|
|
|
|
|
Γ |
0 |
|
|
|
|
|
|
то получим c |
= |
1 |
f (z)dz . Видно, что c |
|
= Res f (z |
|
), т.е. |
|||||
2π i |
|
|
||||||||||
−1 |
|
∫+ |
|
|
−1 |
|
z=z0 |
|
0 |
|
||
|
f (z) |
Γ |
|
|
|
|
|
|
|
|
||
вычет функции |
относительно особой точки |
z0 |
равен ко- |
|||||||||
эффициенту при первой отрицательной степени в разложении функции f (z) в ряд Лорана.
Теорема 1 (Коши). Пусть f (z) есть функция, аналитиче-
ская в замкнутой области E , ограниченной контуром Γ, за исключением конечного числа особых точек zk , k =1,2,Ln , лежащих внутри области. Тогда
|
|
|
|
∫ |
|
|
n |
|
|
|
|
|
f (z)dz =2π i |
∑z=zk |
|||
|
|
|
|
|
k =1 |
Res f (zk ) |
||
|
|
|
|
Γ |
|
|
|
|
|
► |
|
Вокруг точек |
z1, z2 ,K, zn |
опишем окружности |
|||
cρ |
,cρ |
2 |
,K,cρ |
столь малых радиусов ρ1, ρ2 ,K, ρn , чтобы эти ок- |
||||
1 |
|
|
n |
|
|
|
|
|
ружности попарно не пересекались и целиком лежали в области, ограниченной Γ (рис.1).
Рис.1.
Обозначим через Γ* систему контуров, состоящую из контура Γ, проходимого в положительном направлении, и окружностей cρ1 ,cρ2 ,K,cρn , проходимых в отрицательном направлении,
т. е. Γ* = Γ+ +cρ− |
+cρ− |
+L+cρ− . Согласно основной теореме |
1 |
2 |
n |
Коши для многосвязной области имеем
89
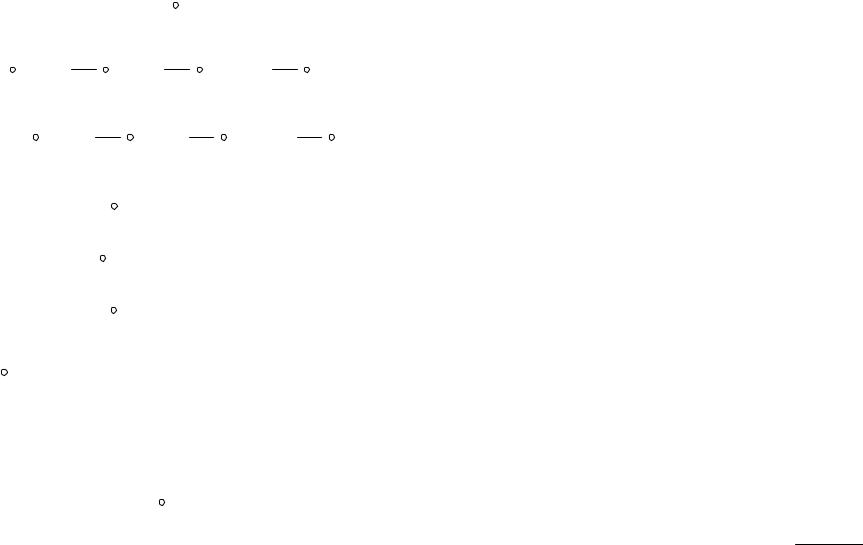
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
∫ f (z)dz = 0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π i |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Γ |
* |
+ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
∫ f (z)dz + |
1 |
∫ f |
(z)dz + |
|
1 |
∫ f |
(z)dzL+ |
|
1 |
∫ f (z)dz =0 . |
|||||||||||||
|
2π i |
|
|
2π i |
2π i |
2π i |
|||||||||||||||||||||
|
|
|
|
+ |
|
|
|
|
− |
|
|
|
|
|
|
− |
|
− |
|
||||||||
|
|
|
|
Γ |
|
|
|
|
|
|
cρ1 |
|
|
|
|
|
|
|
|
|
cρ2 |
|
|
|
cρn |
|
|
|
|
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 |
|
∫ |
f (z)dz = |
1 |
|
∫ f (z)dz + |
1 |
∫ f (z)dzL+ |
1 |
∫ f (z)dz . |
||||||||||||
|
|
|
2π i |
|
2π i |
|
2π i |
2π i |
|||||||||||||||||||
|
|
|
|
|
+ |
|
|
|
+ |
|
|
|
|
|
|
+ |
|
|
+ |
||||||||
|
|
|
|
|
|
|
Γ |
|
|
|
|
cρ1 |
|
|
|
|
|
|
cρ2 |
|
|
|
cρn |
||||
|
|
Так как |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ f (z)dz =2π i ∑Res f (z1 ), |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
k =1 z=z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cρ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ f (z)dz =2π i ∑Res f (z2 ),…, |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
k =1 z =z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cρ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ f (z)dz =2π i ∑Res f (zn ), |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
k =1 z =zn |
|
|
|
|
|
то |
|
|
|
|
|
|
|
|
|
|
cρn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (z)dz = 2π i Res f (z1 )+2π i Res f (z2 )+L+2π i Res f (zn ). ◄ |
|||||||||||||||||||||||
|
|
∫ |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
z =z1 |
|
|
|
|
|
|
|
|
z =z2 |
|
|
|
z =zn |
|
|||||
|
|
Γ+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. Вычисление вычетов функции. |
|
|
|
|
|
||||||||||||||||||||||
|
|
Пусть точка z0 является |
|
изолированной |
особой точкой |
||||||||||||||||||||||
функции |
|
|
f (z). Вычет Res f (z) |
|
в точке z0 можно найти либо по |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
z=z0 |
|
|
|
|
|
|
|
|
|
|
|
|||
формуле |
|
|
Res f (z0 )= |
1 |
|
|
f (z)dz , |
либо |
|
по |
формуле |
||||||||||||||||
|
|
|
2π i |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
z =z0 |
|
|
|
|
∫+ |
|
|
|
|
|
|
|
|
||||
|
|
= Res f (z0 ). |
|
|
|
|
|
|
Γ |
|
|
|
|
|
|
|
|
|
|||||||||
c−1 |
В первом случае нахождение вычета функции |
||||||||||||||||||||||||||
|
|
|
|
|
|
z=z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (z) сводится к вычислению интеграла, во втором случае – к |
||||||||||||||||||||||||||
разложению функции |
|
f (z)в ряд Лорана. Рассмотрим вычисле- |
|||||||||||||||||||||||||
ние вычетов в различных особых точках. |
|
|
|
|
|||||||||||||||||||||||
90
Вычисление вычетов функции относительно устранимой особой точки. Пусть z0 есть устранимая
особая точка функции f (z). В этом случае в разложении в ряд
Лорана отсутствует главная часть. Поэтому Res f (z)= 0 .
z=z0
Вычисление вычетов функции относительно полюса.
Случай 1. Простой полюс.
Пусть точка z0 является простым полюсом функции f (z). Тогда в окрестности точки z0 имеет место разложение в ряд Лорана функции f (z)
|
c−1 |
∞ |
|
f (z)= |
+∑ck (z − z0 )k . |
||
|
|||
|
z − z0 k =0 |
||
Умножая обе части этого равенства на z − z0 , получим
∞
(z − z0 ) f (z)= c−1 +(z − z0 ) ∑ck (z − z0 )k .
k =0
Так как в правой части равенства находится обыкновенный степенной ряд, то его сумма является непрерывной функцией в
точке z0 . Переходя к пределу при z → z0 |
получим |
|
|
|
|||||||||||||
|
|
|
Res f (z0 )=c−1 |
= lim [(z − z0 ) f (z)]. |
|
|
|
||||||||||
|
|
|
z=z0 |
|
|
z→z0 |
|
|
|
|
|
|
|
|
|||
Замечание. Пусть функция |
f (z) есть частное двух аналити- |
||||||||||||||||
ческих в точке z0 функций |
f (z)= |
g(z) |
. где g(z0 )≠ 0 , h(z) име- |
||||||||||||||
h(z) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ет простой нуль в точке z0 , |
h(z0 )=0 , |
h′(z0 )≠ 0 . Тогда точка z0 |
|||||||||||||||
является простым полюсом функции f (z)= |
g(z) |
и |
|
|
|
||||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
(z − z0 ) g(z) |
|
|
|
|
|
h(z) |
|
g(z0 ) |
|
||||
Res |
g(z) |
|
= lim |
= lim |
|
|
g(z) |
= |
. |
||||||||
|
|
|
|
|
|
|
|||||||||||
z=z0 h(z) |
z→z0 |
h(z) |
|
|
z→z0 h(z)−h(z0 ) |
|
h′(z0 ) |
||||||||||
z − z0
Случай 2. Полюс порядка m .
91

Пусть точка z0 является m -кратным полюсом функции f (z). Тогда в окрестности точки z0 имеет место разложение в ряд Ло-
рана функции |
f (z) |
|
|
|
|
|
|
|
|
|
c−m |
|
|
c−m+1 |
|
c−1 |
∞ |
f (z)= |
|
|
+ |
+L+ |
+∑ck (z − z0 )k . |
|||
|
|
m |
m−1 |
|
||||
|
(z − z0 ) |
(z − z0 ) |
z − z0 k =0 |
|||||
Умножая обе части равенства на (z − z0 )m , получим
(z − z0 )m f (z)=
∞
=c−m +c−m+1 (z − z0 )+L+c−1 (z − z0 )m−1 +∑ck (z − z0 )k +m .
k =0
В правой части равенства находится степенной ряд, который равномерно сходится в любом круге, целиком лежащим в его круге сходимости. Поэтому возможно почленное дифференцирование этого ряда любое число раз в круге его сходимости. Дифференцируя последнее равенство (m −1) раз, имеем
d m−1[(z − z0−)m f (z)]= dzm 1
∞
=(m −1)!c−1 +∑ck (k + m) (k + m −1)L(k + 2) (z − z0 )k +1
|
k =0 |
|
|
|
|
|
|
|
|
|
||
Переходя к пределу при z → z0 , получим |
|
|
||||||||||
Res f (z)= c |
|
= |
1 |
|
lim |
d m−1[(z − z0 )m f (z)]. |
||||||
−1 |
(m −1)! |
|||||||||||
z=z0 |
|
|
z→z0 |
dzm−1 |
|
|
||||||
Пример. Найти вычеты функции |
f (z)= |
|
z −4 |
. |
||||||||
|
|
|||||||||||
Решение. |
|
|
|
|
|
|
z3 − z |
|||||
Особыми точками |
данной |
функции являются |
||||||||||
z1 = 0 – полюс второго порядка и z2 =1 – простой полюс. Тогда имеем
Res |
z −4 |
= |
z −4 |
|
= |
z −4 |
|
|
= |
1−4 |
|
= − |
3 |
, |
||
|
|
|||||||||||||||
z3 − z |
|
|
′ |
3z2 −1 |
|
|
3 1−1 |
2 |
||||||||
z=1 |
|
|
3 |
|
|
|
z =1 |
|
|
|
||||||
|
|
(z |
|
− z) |
|
z =1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
92
|
z −4 |
|
1 |
|
2 |
(z − |
4) |
|
″ |
z −4 |
|
″ |
|
3 |
|
′ |
|||||||
|
|
|
|
|
|||||||||||||||||||
|
= |
|
z |
|
|
|
|
|
|
= |
|||||||||||||
Res |
|
3 |
|
|
|
|
|
|
3 |
|
|
|
=lim |
|
|
|
2 |
||||||
z |
− z |
|
lim |
|
z |
− z |
|
|
|
z −1 |
|
= lim |
|
||||||||||
z=0 |
|
|
(2 −1)! z→0 |
|
|
|
|
|
z→0 |
|
|
z→0 |
(z −1) |
|
|
||||||||
=lim |
|
−6 |
|
=6 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(z −1)3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
z→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Вычисление вычетов функции относительно существенно особой точки. Пусть точка z0 является
существенно особой точкой функции f (z). Тогда для вычисления вычета функции f (z) в этой точке непосредственно определяют коэффициент c−1 в разложении функции f (z) в ряд Лорана.
1
Пример. Вычислить вычет функции f (z)= e z .
1
Решение. Точка z =0 является для функции f (z)= e z су-
щественно особой точкой. Разложим данную функцию в ряд Лорана в окрестности точки z =0
1 |
|
1 |
|
1 |
|
|
|
1 |
|
||
e |
z |
=1+ |
+ |
+L+ |
|
+L. |
|||||
z |
2! z2 |
n! zn |
|||||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
|
|||
Отсюда находим Res e |
z |
=1. |
|||||||||
|
|
|
|
|
|
z =0 |
|
|
|||
3. Логарифмический вычет.
Пусть в области E задана однозначная функция f (z), анали-
тическая всюду в E , за исключением конечного числа изолированных особых точек.
Определение 2 . Логарифмической производной
функции f (z) называется функция
(ln f (z))′ = ff ′((zz)) .
Определение 3 . Логарифмическим вычетом аналитической функции f (z) в точке z0 называется вычет в этой точке
логарифмической производной функции f (z):
93
Res(ln f (z))′ = Res |
f ′(z) |
. |
|
|
|||
z =z0 |
z =z0 |
f (z) |
|
Теорема 2. В нулях и полюсах функции f (z), аналитической в
области E , логарифмическая производная (ln f (z))′ имеет полюсы первого порядка. При этом в нуле функции f (z) логарифмический вычет равен порядку нуля функции f (z). а в полюсе – порядку полюса функции f (z), взятому со знаком минус.
Без доказательства.
Теорема 3. Пусть f (z) – мероморфная функция в области
E , Γ – замкнутый кусочно-гладкий контур, целиком лежащий в области E и не проходящий через полюсы и нули функции f (z).
Тогда
2π1 i Γ∫+ ff ′((zz))dz = NΓ −PΓ ,
где NΓ – сумма кратностей нулей функции f (z), лежащих внутри Γ, PΓ – сумма кратностей полюсов функции f (z), ле-
жащих внутри Γ.
► Пусть функция f (z) мероморфна в области E и Γ –
замкнутый кусочно-гладкий контур, целиком лежащий в области E и не проходящий через нули и полюсы функции f (z).
Пусть в области E' E , ограниченной контуром Γ, нулями
функции |
f (z) являются точки |
ξ1,ξ2 ,Kξk кратности |
m1, m2 ,K,mk , полюсами функции |
f (z) являются точки |
|
ζ1,ζ2 ,K,ζt |
кратности n1, n2 ,K, nt . |
|
Применяя к функции (ln f (z))′ основную теорему о вычетах и учитывая теорему 2, получим
2π1 i Γ∫+ ff ′((zz))dz =
= ∑Res ff ′((zz)) = (m1 + m2 +L+ mk )−(n1 + n2 +L+ nt )= Nl − Pl .◄
94
Определение 4 . Логарифмическим вычетом функции f (z) относительно контура Γ называется интеграл
Res[ln f (z)]′ = |
1 |
∫ |
f ′(z)dz . |
||
2π i |
|||||
z=z0 |
l |
+ |
f (z) |
||
|
|
|
|
||
4. Вычет функции относительно точки z = ∞ .
Предположим, что бесконечно удаленная точка z = ∞ является изолированной особой точкой аналитической функции f (z),
т. е. функция f (z) является аналитической в некоторой окрест-
ности бесконечно удаленной точки.
Определение 5 . Вычетом функции f (z) относительно бесконечно удаленной точки z =∞ называется инте-
грал |
1 |
|
|
Res f (z)= |
|
f (z)dz , |
|
2π i |
Γ− |
||
z =∞ |
|
∫ |
|
где Γ — замкнутый кусочно-гладкий контур, целиком лежащий в той окрестности бесконечно удаленной точки, в которой функция f (z) является аналитической.
Здесь интегрирование по контуру Γ совершается в отрицательном направлении, т. е. так, чтобы при обходе контура бесконечно удаленная точка оставалась слева.
В окрестности бесконечно удаленной точки, не содержащей других особых точек функции f (z), кроме самой бесконечно
удаленной точки, разложение функции f (z) в ряд Лорана имеет
вид
∞
f (z)= ∑ck zk .
k =−∞
Так как ряд Лорана функции f (z) сходится равномерно на
контуре Γ, то этот ряд можно интегрировать почленно вдоль контура Γ.
Учитывая, что для k = 0,1,±2,L ∫zk dz = 0 и |
∫dz |
= −2π i , то |
|
Γ− |
Γ− |
z |
|
после интегрирования вдоль контура |
Γ |
|
равенства |
95 |
|
|
|

∞ |
|
∫ f (z)dz = −2π i c−1 . |
|
f (z)= ∑ck zk , |
получим |
Отсюда |
|
k =−∞ |
|
l − |
|
Res f (z)= −c−1 .
z=∞
Таким образом, вычет функции f (z) относительно бесконеч-
но удаленной точки равен взятому с противоположным знаком коэффициенту при первой отрицательной степени в разложении Лорана в окрестности бесконечно удаленной точки функции.
Теорема 4. |
Если f (z) |
– функция, аналитическая в каждой |
|||||||||||
точке расширенной плоскости C , за исключением конечного |
|||||||||||||
числа изолированных особых точек, то |
|
|
|
||||||||||
|
|
∑n |
Res f (z)+ Res f (z)= 0 . |
|
|||||||||
|
|
k =1 |
z =z |
k |
z=∞ |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
► Опишем из точки |
z =0 |
окружность такого радиуса R , |
|||||||||||
чтобы все особые точки z1, z2 ,K, zn |
|
функции |
f (z), за исключе- |
||||||||||
нием бесконечно удаленной точки |
|
z =∞, |
лежали внутри этой |
||||||||||
окружности. Тогда по основной теореме о вычетах имеем |
|||||||||||||
|
|
∫ |
f (z)dz =2π i |
|
n |
Res f |
(z |
|
). |
||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
∑z =zk |
|
k |
|
|||
|
|
Γ+ |
|
|
|
|
|
k =1 |
|
|
|
||
|
1 |
|
|
|
n |
|
|
|
|
|
|
|
|
Отсюда |
f (z)dz = |
|
Res f (z |
|
). |
|
|
|
|||||
2π i |
|
|
|
|
|
||||||||
|
∫+ |
|
|
∑z =zk |
|
|
k |
|
|
|
|
||
|
|
Γ |
|
|
k =1 |
|
|
|
|
|
|
|
|
По определению вычета относительно бесконечно удаленной
точки имеем |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Res f (z)= |
|
|
|
f (z)dz . |
|
|||
|
|
|
|
|
2π i |
Γ− |
|
||||||
|
|
|
|
|
|
z =∞ |
|
|
|
|
∫ |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
Тогда ∑Res f (z)+ Res f (z)= 0 .◄ |
|
|
|
||||||||||
|
k =1 |
z=z |
k |
|
z=∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример. |
|
|
Найти |
сумму |
|
|
вычетов |
функции |
|||||
f (z)= |
|
z |
6 |
|
относительно всех ее особых точек, рас- |
||||||||
(z2 + 4)2 |
(z2 +1)3 |
|
|||||||||||
положенных в комплексной плоскости.
96
Решение. Особыми точками данной функции являются: z1,2 = ±2i – полюсы второго порядка, z3,4 = ±i – полюсы третьего порядка.
Применение основной теоремы теории вычетов связано с большими вычислениями. Для решения этого примера удобнее воспользоваться теоремой 4. Видно, что в бесконечно удаленной точке функция f (z) имеет нуль первого порядка. Правильная
часть ее разложения в ряд Лорана начинается с члена 1z .
Следовательно, Res |
|
z6 |
|
= −1 . |
||
(z2 + 4)2 (z2 +1)3 |
||||||
|
z=∞ |
|
||||
4 |
|
z6 |
|
|
|
|
Тогда ∑Res |
|
|
|
=1 . |
|
|
|
2 |
3 |
|
|||
k =1 z=zk |
(z2 + 4) (z2 |
+1) |
|
|
||
Вопросы для самоконтроля
1.Что называется вычетом функции?
2.Сформулируйте и докажите основную теорему о вычетах.
3.Как вычисляется вычет относительно устранимой точки?
4.Как вычисляется вычет относительно простого полюса?
5.Как вычисляется вычет относительно полюса порядка m ?
6.Как вычисляется вычет относительно существенно особой точки?
7.Что называется логарифмическим вычетом?
8.Как вычисляется вычет относительно бесконечно удаленной точки?
97
